- Double Produit De Quaternions
-
Double produit de quaternions
Il est possible de calculer un double produit de quaternions, c'est-à-dire une expression de la forme :
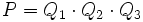 ,
,dans laquelle il n'est pas nécessaire d'écrire des parenthèses puisque le produit est associatif.
Intéressons-nous au cas particulier dans lequel les quaternions extrêmes
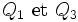 sont inverses l'un de l'autre et utilisons les notations de type
sont inverses l'un de l'autre et utilisons les notations de type 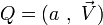 pour représenter les 3 quaternions :
pour représenter les 3 quaternions :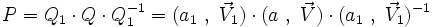
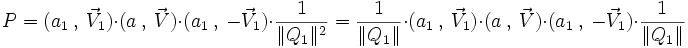
.
Comme les quaternions
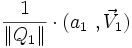 et son inverse
et son inverse 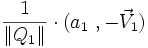 sont unitaires, on peut les écrire sous la forme
sont unitaires, on peut les écrire sous la forme 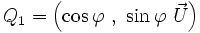 et
et 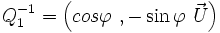 , d'où l'écriture :
, d'où l'écriture :
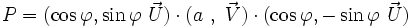
En tenant compte de la distributivité du produit, on peut écrire :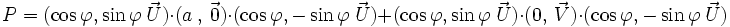
Ainsi le quaternion
 se décompose en
se décompose en 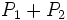 avec :
avec :
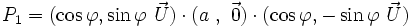 et
et
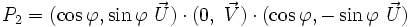
Comme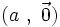 est un scalaire pur, le double produit représenté par
est un scalaire pur, le double produit représenté par 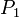 est commutatif et peut s'écrire plus simplement :
est commutatif et peut s'écrire plus simplement :
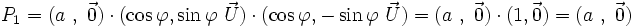 .
.
Par conséquent, on a :
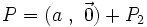 avec
avec 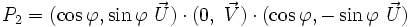 .
.Portons donc notre attention sur le quaternion
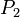 en développant d'abord le premier produit, puis le second ; il vient d'abord :
en développant d'abord le premier produit, puis le second ; il vient d'abord :
![P_2 = \left[-\sin \varphi\ (\vec U\cdot \vec V), \cos \varphi\ \vec V+\sin \varphi\ (\vec U\wedge\vec V)\right]\cdot \left[\cos \varphi, -\sin \varphi\ \vec U\right]](/pictures/frwiki/51/3f7cb1035f78620c9eafe2f6f324e8d2.png) , puis :
, puis :
![\begin{matrix}P_2 = \big[ &-&\sin \varphi\ \cos \varphi\ (\vec U\cdot \vec V) &+& \sin \varphi\ \cos \varphi\ (\vec V\cdot \vec U) &+& \sin^2 \varphi\ (\vec U\wedge\vec V)\cdot \vec U,&\ \\\ &+& \sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U &+& \cos^2\varphi\ \vec V &+& \sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V)&\ \\&-& \sin \varphi\ \cos \varphi\ (\vec V\wedge\vec U) &-& \sin^2\varphi\ (\vec U\wedge \vec V)\wedge \vec U&\ &\ &\big] \end{matrix}](/pictures/frwiki/98/b7f1d76f1af2d98446e61654dbe6c5d9.png)
En éliminant le produit mixte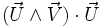 (qui est nul) et en développant le double produit vectoriel
(qui est nul) et en développant le double produit vectoriel 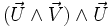 , on obtient :
, on obtient : ![P_2 = \Bigg[0 \ ,\ \sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U +\ \cos^2\varphi\ \vec V + 2\sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V) - sin^2\varphi\ \left[(\vec U\cdot \vec U)\ \vec V - (\vec V\cdot \vec U)\ \vec U
\right]\Bigg]](/pictures/frwiki/99/c9fb60a405d1083c756cd9ea979f1fda.png)
puis successivement :
![P_2 = \Bigg[0 \ ,\ 2\sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U +
\left[\cos^2\varphi\ - \sin^2\varphi\ (\vec U\cdot \vec U)\right]\,\vec V\ +\ 2\sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V) \Bigg]](/pictures/frwiki/97/a51f4068030bf2996b25c494126be9b6.png)
![P_2 = \Bigg[0 \ ,\ 2\sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U +
\left[\cos^2\varphi\ - \sin^2\varphi\right]\vec V\ +\ 2\ \sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V) \Bigg]](/pictures/frwiki/51/3813f1ae98b62e5234e77e9131df5788.png)
![P_2 = \left[0 \ ,\ \cos 2\,\varphi\ \, \vec V\ +
\ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U +
\ \sin 2\,\varphi\ (\vec U\wedge\vec V) \right]](/pictures/frwiki/48/0feefeb8cdb47d4baf27d3db8a279e11.png)
Ainsi, il est établi que si le vecteur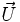 est unitaire, l'égalité suivante est toujours vérifiée :
est unitaire, l'égalité suivante est toujours vérifiée :![(\cos \varphi, \sin \varphi \ \vec U)\cdot (a\ ,\ \vec V)\cdot (\cos \varphi, -\sin \varphi \ \vec U) = (a\ ,\ \vec 0) + \left[0 \ ,\ \cos 2\,\varphi\ \, \vec V\ + \ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U + \ \sin 2\,\varphi\ (\vec U\wedge\vec V) \right]](/pictures/frwiki/55/7832e13022fd5d43d7f604778466a4ed.png) ,
,Or, dans l'expression qui apparaît dans la composante vectorielle du deuxième quaternion du membre de droite de cette égalité, à savoir :
![\cos 2\,\varphi\ \, \vec V\ + \ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U + \ \sin 2\,\varphi\ (\vec U\wedge\vec V)]](/pictures/frwiki/100/d430fabc9b7eed0351675865c097b89c.png) ,
,on peut reconnaître l'expression vectorielle du vecteur transformé du vecteur
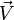 dans la rotation
dans la rotation ![\mathbf R\left[2\,\varphi\,\,; \vec U\right]](/pictures/frwiki/55/7fbb38e15013d3d30e9c54df429d3d5a.png) d'angle
d'angle 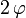 et d'axe orienté
et d'axe orienté 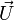 normé.
normé.
De la démonstration précédente, on peut tirer l'importante conclusion générale suivante :
Conclusion
Dans la rotation
![\mathbf R\left[2\,\varphi\,\,; \vec U\right]](/pictures/frwiki/55/7fbb38e15013d3d30e9c54df429d3d5a.png) d'angle
d'angle 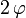 et d'axe orienté
et d'axe orienté 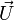 normé,
normé,
le transformé![\vec V' = \mathbf R_{\left[2\varphi, \vec U\right]}(\vec V)\,](/pictures/frwiki/52/4ff355d36ac46fcc03852c720b405e0c.png) de tout vecteur
de tout vecteur 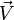 peut être calculé :
peut être calculé :- soit grâce à l'égalité quaternionique suivante :
![\left(0 \ ,\ \mathbf R_{\left[2\varphi, \vec U\right]}(\vec V)\right) = (\cos \varphi, \sin \varphi \ \vec U)\cdot (0,\ \vec V)\cdot (\cos \varphi, -\sin \varphi \ \vec U)\ \ \ \,](/pictures/frwiki/101/ef0b1e8d06cd87c686ace332438342f9.png) (formule n° 1)
(formule n° 1)- soit grâce à l'égalité vectorielle :
![\mathbf R_{\left[2\varphi, \vec U\right]}(\vec V) = \cos 2\,\varphi\ \, \vec V\ + \ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U + \ \sin 2\,\varphi\ (\vec U\wedge\vec V)\ \ \ \,](/pictures/frwiki/54/6299e2651b01ca0ba64b34833bafcb3d.png) (formule n° 2)
(formule n° 2)
Articles de mathématiques en rapport avec la notion de nombre Définition des nombres · Entiers naturels · Entiers relatifs · Nombres transfinis · Nombres décimaux · Nombres rationnels · Nombres constructibles · Nombres algébriques · Nombres transcendants · Nombres calculables · Nombres réels · Nombres complexes · Nombres hypercomplexes · Quaternions · Octonions · Sédénions · Nombres hyperréels · Nombres surréels · Nombres ordinaux · Nombres cardinaux · Nombres p-adiques · Nombres normaux · Suite d'entiers · Constantes mathématiques · Grands nombres · Infiniments petits · Infini - Portail des mathématiques
Catégories : Nombre hypercomplexe | Algèbre - soit grâce à l'égalité quaternionique suivante :
Wikimedia Foundation. 2010.
