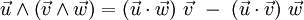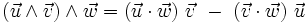- Géométrie vectorielle
-
Calcul vectoriel en géométrie euclidienne
Cet article traite des opérations portant sur les vecteurs en géométrie euclidienne.
Sommaire
Opérations sur les vecteurs dans le plan et l'espace
Les vecteurs dont il sera question dans cet article sont ceux de l'espace
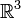 ou du plan
ou du plan 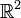 .
.Comme souligné ci-dessus, certaines constructions géométriques sont spécifiques aux vecteurs. Ces constructions géométriques ayant des propriétés communes avec les opérations sur les nombres (addition, multiplication), on adopte une notation similaire.
Produit d'un vecteur par un scalaire
Le terme « scalaire » désigne ici un nombre réel. Le produit d'un vecteur
 par un scalaire a est un vecteur noté
par un scalaire a est un vecteur noté- de même direction et sens que
 , mais dont la longueur vaut
, mais dont la longueur vaut
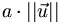 , si a > 0
, si a > 0
- de même direction mais de sens contraire que
 , et dont la longueur vaut
, et dont la longueur vaut
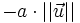 , si a < 0.
, si a < 0.
- il s'agit d'un vecteur nul si a = 0
Il s'agit d'une dilatation (si |a| >1) ou d'une contraction (si |a| <1), bref d'une homothétie de rapport a.
On a
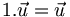 ,
, 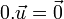 et
et 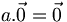
1 est donc l'élément scalaire neutre, et 0 l'élément scalaire absorbant pour cette opération. Le produit d'un vecteur par un scalaire est distributif sur l'addition des scalaires
mais il n'est pas commutatif : la notation
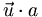 n'a pas de sens.
n'a pas de sens.Notez que deux vecteurs sont colinéaires (parallèles) si et seulement s’ils sont proportionnels, c'est-à-dire s'il existe un nombre a tel que
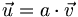 .
.Somme de deux vecteurs
La somme de deux vecteurs
 et
et  est un vecteur, noté
est un vecteur, noté 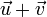 , qui est construit de la manière suivante :
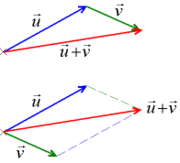
, qui est construit de la manière suivante :- on amène l'origine du deuxième vecteur à l'extrémité du premier, la somme est le vecteur qui joint l'origine du premier vecteur à l'extrémité de second.
Il s'agit du troisième côté d'un triangle formé par les deux premiers vecteurs.
On peut aussi le construire d'une autre manière :
- on amène les origines des deux vecteurs en un même point, on trace un parallélogramme dont les vecteurs sont deux côtés, la somme est alors la diagonale du parallélogramme partant de l'origine.
Dans les deux cas, on place les vecteurs bout-à-bout ; mais si l'origine d'un vecteur correspond à l'extrémité de l'autre, on utilise la méthode du triangle, si les origines sont confondues, on utilise la méthode du parallélogramme.
Si l'on a trois points A, B et C, alors on a la « relation de Chasles » :
on déduit de cela que
ce qui permet de définir l'opposé d'un vecteur, et donc la soustraction : en posant la notation
on a
L'opposé d'un vecteur est le vecteur de même direction, de même longueur, mais de sens opposé.
On a :
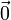 est l'élément neutre de l'addition des vecteurs. L'addition des vecteurs est commutative
est l'élément neutre de l'addition des vecteurs. L'addition des vecteurs est commutativeLe produit d'un scalaire par un vecteur est distributif sur l'addition des vecteurs :
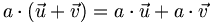 .
.
Produit scalaire de deux vecteurs
Définition
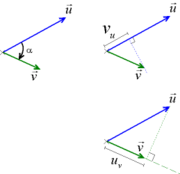
Si
 et
et  sont deux vecteurs faisant un angle géométrique α, le produit scalaire, noté
sont deux vecteurs faisant un angle géométrique α, le produit scalaire, noté 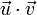 , est le nombre (réel) valant :
, est le nombre (réel) valant : .
.
Le produit scalaire est nul si l'un des vecteurs est nul ou si l'angle entre eux est droit (c’est-à-dire si et α = π/2 rad = 90 °), les vecteurs
 et
et  sont dans ce cas orthogonaux, strictement positif si l'angle est aigu et strictement négatif si l'angle est obtus.
sont dans ce cas orthogonaux, strictement positif si l'angle est aigu et strictement négatif si l'angle est obtus.Cette opération a été introduite pour simplifier les calculs sur les projections orthogonales. En effet, si vu est la longueur algébrique de la projection de
 sur une droite orientée selon
sur une droite orientée selon  (vu est positif si la projection est dans le même sens que
(vu est positif si la projection est dans le même sens que  , négatif s'il est dans le sens opposé), alors on a
, négatif s'il est dans le sens opposé), alors on aAinsi, si la norme de
 vaut 1, alors la longueur algébrique de la projection orthogonale de
vaut 1, alors la longueur algébrique de la projection orthogonale de  sur la droite est
sur la droite est 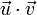 . De la même manière, si uv est la longueur algébrique de la projection de
. De la même manière, si uv est la longueur algébrique de la projection de  sur une droite orientée selon
sur une droite orientée selon  ,alors on a
,alors on aPropriétés
- Le produit scalaire est symétrique
- Il est distributif sur l'addition des vecteurs
- Le vecteur nul est l'élément absorbant du produit scalaire
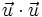 s'appelle le carré scalaire du vecteur
s'appelle le carré scalaire du vecteur  et se note
et se note  2 ; ainsi :
2 ; ainsi :  2 =
2 = 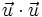
- Le carré scalaire d'un vecteur est égal au carré de sa norme
 2 =
2 = 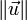 2 et donc
2 et donc 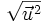 =
= 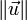
- Deux vecteurs non nuls sont orthogonaux si et seulement si leur produit scalaire est nul
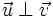 si et seulement si
si et seulement si 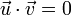
- Dans le plan rapporté à une base orthonormale
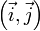
Démonstration- Dans l'espace rapporté à une base orthonormale
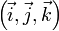
Voir aussi ( pour une définition générale valable dans toutes les branches des mathématiques )
Produit vectoriel de deux vecteurs dans l'espace
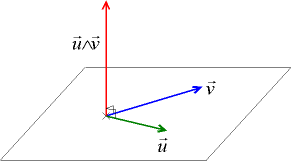 Produit vectoriel
Produit vectorielNotons tout d'abord que deux vecteurs non colinéaires
 et
et  définissent un plan vectoriel ; un troisième vecteur
définissent un plan vectoriel ; un troisième vecteur 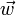 est coplanaire aux deux précédents si et seulement s'il peut s'écrire comme une combinaison linéaire des deux premiers, c'est-à-dire s'il existe deux réels a et b tels que
est coplanaire aux deux précédents si et seulement s'il peut s'écrire comme une combinaison linéaire des deux premiers, c'est-à-dire s'il existe deux réels a et b tels queTrois vecteurs non coplanaires forment une base. La base
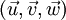 est dite directe si on peut l'imager avec la main droite,
est dite directe si on peut l'imager avec la main droite,  étant le pouce,
étant le pouce,  étant l'index et
étant l'index et 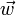 étant le majeur.
étant le majeur.On définit le produit vectoriel des deux vecteurs
 et
et  , noté
, noté 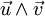 , comme étant le vecteur :
, comme étant le vecteur :- normal au plan vectoriel de base
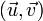
- dont la norme vaut
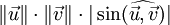
- tel que
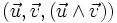 forme une base directe.
forme une base directe.
On étend la définition précédente au cas où
 et
et  sont colinéaires en posant :
sont colinéaires en posant :- Remarque
Le produit vectoriel agit sur des objets mathématiques de différentes sortes, soit des vecteurs, soit des pseudovecteurs. Cette distinction est peu importante en base orthonormée (sauf pour les symétries), mais si elle n'est pas faite en base non orthonormée, cela aboutit à des absurdités. On a ce problème en physique avec notamment les champs magnétiques et les moments, qui ressemblent beaucoup aux vecteurs, mais qui sont en fait des pseudovecteurs, et n'obéissent pas aux mêmes règles de calcul.
Produit mixte
Définition et propriétés
Étant donnés trois vecteurs
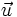 ,
, 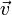 et
et 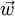 , on appelle produit mixte de ces 3 vecteurs la quantité :
, on appelle produit mixte de ces 3 vecteurs la quantité :![\left[\vec u, \vec v, \vec w\right] = (\vec u \wedge \vec v) \cdot \vec w\,](/pictures/frwiki/101/e3e94bd42adeb89556d444a062b694c4.png) .
.
On peut démontrer que l'on a :
et
et aussi :
![\left[\vec u, \vec v, \vec w\right] = \begin{vmatrix}
u_x & u_y & u_z\\v_x & v_y & v_z\\w_x & w_y & w_z \end{vmatrix}](/pictures/frwiki/52/4f9e150129fca86f8f9a817603d4a6a4.png)
autrement dit :
![\left[\vec u, \vec v, \vec w\right] = (u_x v_y w_z + v_x w_y u_z + w_x u_y v_z) - (u_z v_y w_x + v_x w_z u_y + w_y u_x v_z)\,](/pictures/frwiki/53/56b2d64ea817a9f73e683384852d4384.png)
Remarques :- Si deux des trois vecteurs sont égaux ou colinéaires, le produit mixte est nul.
- Le produit mixte de trois vecteurs vrais (en opposition à des pseudovecteurs) est une quantité pseudoscalaire.
Application du produit mixte
- Si les vecteurs
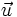 ,
, 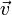 et
et 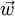 ont même origine, la valeur absolue du produit mixte
ont même origine, la valeur absolue du produit mixte ![\left[\vec u, \vec v, \vec w\right]\,](/pictures/frwiki/98/b03580ab9cbe8ad1222dfafc855ee3e4.png) est égale au volume du parallélépipède construit sur
est égale au volume du parallélépipède construit sur 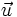 ,
, 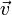 et
et 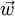 , ou encore à six fois le volume du tétraèdre construit sur ces mêmes vecteurs.
, ou encore à six fois le volume du tétraèdre construit sur ces mêmes vecteurs.
Double produit vectoriel
On peut combiner trois vecteurs
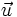 ,
, 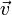 et
et 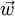 par deux produits vectoriels successifs. C'est le double produit vectoriel.
par deux produits vectoriels successifs. C'est le double produit vectoriel.Exemple :
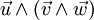
Comme le produit vectoriel n'est ni associatif, ni commutatif, il est nécessaire d'utiliser ici des parenthèses et le résultat va dépendre à la fois de l'ordre dans lequel les opérations sont effectuées et de l'ordre de présentation des 3 vecteurs.
On peut démontrer (sans difficulté mais assez laborieusement) les 2 formules suivantes :
et
Articles connexes
- Base
- Espace vectoriel
- Géométrie euclidienne | Géométrie dans l'espace | Géométrie analytique
- Produit scalaire | Produit vectoriel | produit mixte
- Déterminant
- Pseudovecteur
- Portail de la géométrie
Catégories : Page à recycler (mathématiques) | Géométrie
Wikimedia Foundation. 2010.

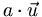
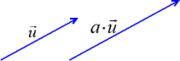
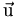
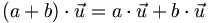
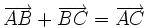
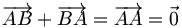
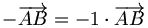
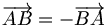
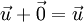
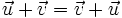
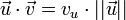
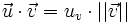
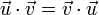
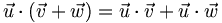
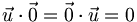
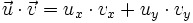
 .
. 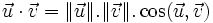
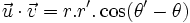
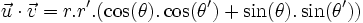
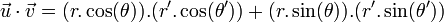
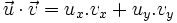
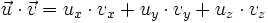
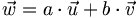
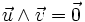
![\left[\vec u, \vec v, \vec w\right] =
\left[\vec v, \vec w, \vec u\right] =
\left[\vec w, \vec u, \vec v\right]\,](/pictures/frwiki/50/2de66ecb34ed99f1843a1bff308ee501.png)
![\left[\vec v, \vec u, \vec w\right] =
\left[\vec w, \vec v, \vec u\right] =
\left[\vec u, \vec w, \vec v\right] =
- \left[\vec u, \vec v, \vec w\right]\,](/pictures/frwiki/100/d8d1d2a868d9c23b9695708d8f1c7989.png)