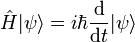ℎ

ℎ

Constante de Planck

Page d'aide sur l'homonymie Pour les articles homonymes, voir Planck.
Cet article fait partie de la série
Mécanique quantique
\hat H | \psi\rangle = i\hbar\frac{{\rm d}}{{\rm d}t}|\psi\rangle
Postulats de la mécanique quantique

Histoire de la mécanique quantique

En physique, la constante de Planck, notée h, est une constante utilisée pour décrire la taille des quanta. Elle joue un rôle central dans la mécanique quantique et a été nommée d'après le physicien Max Planck.

La constante de Planck, notée 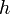h\, relie notamment l’énergie d’un photon à sa fréquence 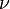\nu\, (lettre grecque nu) :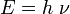

E=h\ \nu\,

Sommaire

Valeur

Dans les unités SI, le CODATA de 2006 recommande la valeur suivante :

h ≈ 6,626 0 755×10-34  J.s,

avec une incertitude standard de ±0,000 000 33×10-34  J.s, soit une incertitude relative de 5,0×10-8.

Constante de Planck réduite ou de Dirac

La constante de Planck possède les dimensions d’une énergie multipliée par un temps. Il est possible d’écrire ces unités sous la forme d’une quantité de mouvement par une longueur (kg·mètre2·s-1) c’est-à-dire les mêmes unités que le moment angulaire.

Une grandeur associée est le quantum d’action, également appelé constante de Planck réduite ou encore parfois constante de Dirac, notée ħ et prononcée « h barre » :

  • Valeur en joules-secondes :
    ħ = h / 2 π ≈ 1,054 571 628×10-34  J.s,
    avec une incertitude standard de ±0,000 000 053×10-34  J.s.
  • Valeur en électron-volts-secondes :
    ħ ≈ 6,582 118 99×10-16  eV.s,
    avec une incertitude standard de ±0,000 000 16×10-16  eV.s, soit une incertitude relative de 2,5×10-8.
  • Valeur en MeV-fermis :
    ħ c ≈ 197,326 963 1  MeV.fm,
    avec une incertitude standard de ±0,000 004 9  MeV.fm, soit une incertitude relative de 2,5×10-8.

Interprétation physique

La constante de Planck est utilisée pour décrire les phénomènes de quantification qui se produisent avec les particules et dont certaines propriétés physiques ne prennent que des valeurs multiples de valeurs fixes au lieu d'un ensemble continu de valeurs possibles. Par exemple, l'énergie d'une particule est reliée à sa fréquence 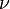\nu\, par :

E = h\ \nu\,.

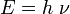On retrouve de telles conditions de quantification dans toute la mécanique quantique. Par exemple, si 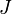J\, est le moment angulaire total d’un système et 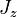J_z\, le moment angulaire du système mesuré sur une direction quelconque, ces quantités ne peuvent prendre que les valeurs :

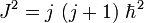  • J^2 = j\ (j + 1)\ \hbar^2, avec : 2j = 0, 1, 2, 3, 4, ...
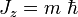  • J_z = m\ \hbar, avec : m = -j, -j+1, ..., j-1, j.

En conséquence, 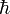\hbar\, est parfois considérée comme un quantum de moment angulaire puisque le moment angulaire de n’importe quel système, mesuré par rapport à n'importe quel choix particulier d'axe, est toujours un multiple entier de cette valeur.

La constante de Planck réduite apparaît également dans les énoncés du principe d'incertitude de Heisenberg. L’écart type d’une mesure de position 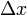\Delta x\, et celui d’une mesure de quantité de mouvement le long du même axe 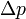\Delta p\, obéissent à la relation suivante :

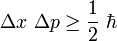\Delta x\ \Delta p \ge \frac{1}{2}\ \hbar.

La constante de Planck réduite 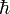\hbar est également employée dans le système d’unités dit des unités de Planck.

Première et seconde constantes de Planck de luminance

Dans la théorie des corps noirs, notamment pour l'expression de la luminance, on utilise deux autres constantes de Planck appelées C1 et C2 :

  • C1 = 3,7415×10-16  W⋅m2⋅sr-1, soit C1 = 1 1 905×10-16  W⋅m2
  • C2 = 1 4 388×10-2  m⋅K

Représentation informatique

La constante de Planck possède les représentations Unicode suivantes :

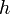  • h\, : U+210E (constante de Planck) ;
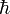  • \hbar\, : U+210F (constante de Planck réduite sur 2π) ;
  • en LaTeX, 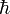\hbar \, s'écrit \hbar.

Voir aussi

Liens externes

Liens internes

  • Portail de la physique Portail de la physique
Ce document provient de « Constante de Planck ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article ℎ de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”