Représentations graphiques de données statistiques

Les résultats d'une enquête statistique peuvent donner lieu à de nombreuses représentations graphiques.

Représentation des effectifs et des fréquences.

Une règle générale distingue les représentations sans épaisseur (diagramme en bâtons) et les représentations avec épaisseur : dans une représentation sans épaisseur, l'effectif (ou la fréquence) est proportionnel à la hauteur, tandis que dès qu'une surface existe, l'effectif (ou la fréquence) est proportionnel à l'aire.

Variables discrètes

Variables quantitatives discrètes

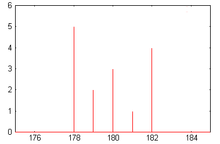Diagramme en bâtons issu de l'article Statistiques élémentaires discrètes

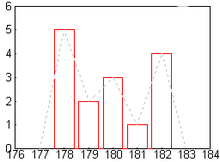
Pour des variables quantitatives discrètes, on privilégie le diagramme en bâtons, mais on voit apparaître parfois des représentations avec épaisseur.

• Diagramme figuratif : Les effectifs sont représentés par des images (silhouettes, bâtiments, etc.) évoquant la population étudiée. Ces images ont une surface proportionnelle à l'effectif. Notons que, si la surface est proportionnelle, ce n'est pas le cas de la hauteur ni de la largeur de l'image (doubler la longueur et la hauteur, par exemple, multiplie la surface par 4, non par 2 ; pour doubler la surface, il faut multiplier la hauteur et la largeur par √2, soit 1,414…, non par 2).

Diagramme en rectangle avec lissage

• Diagramme en rectangles : si la base des rectangles a la même taille, les hauteurs proportionnelles aux effectifs respectent la règle des aires.
• Ajout d'un polygone rejoignant les sommets du diagramme en bâtons. Cette tentative de lissage de la représentation graphique ne respecte pas tout à fait la règle des aires (l'aire sous le polygone ne correspond pas tout à fait à l'effectif ou la fréquence) mais a le mérite de présenter une courbe se rapprochant de la courbe de densité de probabilité.

Variables qualitatives

Diagramme en camembert

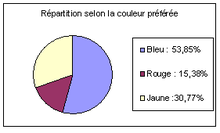
Pour des variables qualitatives, on utilise fréquemment les diagrammes circulaires dits « en camembert », demi-circulaire ou rectangulaire. On trouve aussi des diagrammes figuratifs avec le danger évoqué plus haut.

Variables continues

Article détaillé : Histogramme.

Histogramme avec lissage

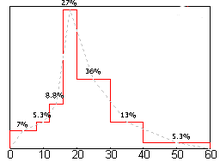
On utilise l'histogramme en respectant la règle des aires. Pour éviter tout danger, il est préférable de travailler avec des classes d'amplitude constante. Dans ce cas, les hauteur des rectangles sont proportionnelles aux effectifs (ou aux fréquences). Le cas des classes d'amplitudes variables se révèle plus délicat et est traité dans statistiques élémentaires continues. On trouve aussi pour les variables continues la même tentative de lissage avec la même réserve sur la règle des aires.

Représentation des effectifs cumulés.

Polygone des fréquences cumulées avec lecture de quartiles

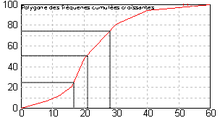
Pour les variables continues, on peut tracer le polygone des effectifs (ou fréquences) cumulés. Le principe du tracé est expliqué dans l'article statistiques élémentaires continues. Ce polygone, permet de lire très rapidement l'effectif d'un intervalle de la forme [x₁,x] et , par différence, l'effectif de tout intervalle. Elle permet aussi de lire très rapidement les quartiles et les déciles. Cette représentation préfigure le tracé de la fonction de répartition en probabilité.

On voit apparaître parfois un polygone des effectifs cumulés pour des variables discrètes. En toute rigueur, il faudrait tracer un diagramme en escalier.

Nuage de points

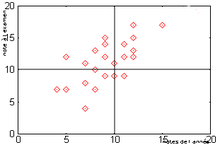
Exemple de nuage de points

On rencontre principalement cette représentation dans les séries statistiques à deux variables. Elle apparaît aussi de manière moins identifiable dans les cartes géographiques ou météorologique (impact de la foudre, densité de population, présence d'industries,...). L'effectif est alors associé à une taille de point ou une couleur de fond.

Diagramme en boîte à moustaches

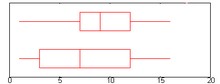
Exemple de diagramme en boîte à moustaches

Le diagramme en boîte à moustaches résume seulement quelques caractéristiques de position du caractère étudié (médiane, quartiles, min/max ou déciles). Il est utilisé principalement pour comparer un même caractère dans deux populations de tailles différentes. Il s'agit de tracer un rectangle allant du premier quartile au troisième quartile et coupé par la médiane. On ajoute parfois des segments aux extrémités menant jusqu'aux valeurs min/max ou jusqu'au premier et neuvième décile. On parle alors de diagramme en boîte à moustaches ou à pattes.

Sparklines

Les sparklines sont un format développé par Edward Tufte pour des mini-graphiques qui peuvent être insérés dans un texte sur une page.

Tufte décrit les sparklines comme des "graphiques intenses en données, de design simple, et ayant la taille d’un mot". Alors que le graphique typique est conçu de manière à montrer le plus de données possible et qu'il est placé hors du flux de texte, les sparklines sont concis, mémorisables, et localisés précisément à l’endroit approprié.

Sparklines U.S. stock market activity (February 7, 2006)
Day	Index	Value	Change
	Dow Jones	10765.45	−32.82 (−0.30%)
	S&P 500	1256.92	−8.10 (−0.64%)
	Nasdaq	2244.83	−13.97 (−0.62%)

Historique

Les graphiques n’apparaissent qu’avec le développement de la statistique et les progrès de l'imprimerie à la fin du XVIII^e siècle. Il se produit une lente évolution depuis les tableaux de chiffres alors en usage, vers des tableaux semi-graphiques comme le tableau du docteur Quesnay. Les premières méthodes de représentation véritablement graphiques sont issues d'une publication de Joseph Priestley, A Chart of Biography (1765), et des atlas de William Playfair et d’Emmanuel de Las Cases (1799).

Articles connexes

• Représentation graphique
• Statistiques
• Statistique (mathématiques élémentaires)

• Portail des probabilités et des statistiques