- Systeme d'equations (mathematiques elementaires)
-
Système d'équations (mathématiques élémentaires)

Cet article fait partie de la série
Mathématiques élémentairesAlgèbre Logique Arithmétique Probabilités Statistiques Un système d'équations est un ensemble de plusieurs équations faisant appel aux mêmes inconnues.
Dans la vie courante et en sciences, les phénomènes dépendent le plus souvent de plusieurs paramètres. Pour les modéliser, on utilise en mathématiques les systèmes d'équations à plusieurs inconnues. Un problème mathématique comportant moins d'équations que d'inconnues a une infinité de solutions.
Sommaire
Exemple d'équation avec une infinité de solutions
L'équation
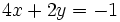 a une infinité de solutions. Si je prends pour
a une infinité de solutions. Si je prends pour  la valeur
la valeur 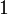 , j'obtiens :
, j'obtiens :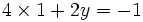
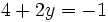
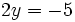 ;
;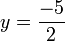 .
.
Plus généralement, si
 est un nombre quelconque,
est un nombre quelconque, 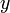 doit absolument valoir
doit absolument valoirDéfinitions mathématiques
On appelle système d'équations un ensemble
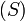 de plusieurs équations à plusieurs inconnues que l'on doit résoudre en même temps.
de plusieurs équations à plusieurs inconnues que l'on doit résoudre en même temps.Exemple :
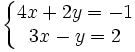 est un système de deux équations à deux inconnues.
est un système de deux équations à deux inconnues.Résoudre
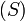 , c'est trouver toutes les valeurs qu'il faut donner à chaque inconnue en même temps pour que toutes les égalités soient vraies.
, c'est trouver toutes les valeurs qu'il faut donner à chaque inconnue en même temps pour que toutes les égalités soient vraies.Le système
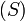 est linéaire s'il existe des nombres réels
est linéaire s'il existe des nombres réels 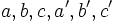 tels que
tels que 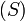 soit de la forme :
soit de la forme : .
.Systèmes de 2 équations linéaires à 2 inconnues
Interprétation graphique
Celle-ci va nous permettre d'établir des théorèmes utiles pour la suite.
Chaque équation du système définit une fonction affine, et est donc représentée par une droite dans un repère.Or :
définit une fonction affine, et est donc représentée par une droite dans un repère.Or :- les coordonnées du point d'intersection des deux droites représentent la solution de
 ;
; - deux droites ont :
- soit un unique point d'intersection ;
- soit aucun point d'intersection ;
- soit une infinité de points d'intersection.
D'où le théorème suivant :
Théorème 1 : Un système de 2 équations linéaires à 2 inconnues a :
- soit une unique solution ;
- soit aucune solution ;
- soit une infinité de solutions.
On démontre aussi le théorème suivant (en se reportant plus haut pour les notations) :
Théorème 2 : Un système de 2 équations linéaires à 2 inconnues admet une seule solution si, et seulement si, le nombre
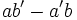 est non nul, c'est-à-dire :
est non nul, c'est-à-dire :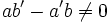 .
.On appelle
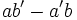 le déterminant du système (S).
le déterminant du système (S).Exemple de résolution graphique : Soit le système :
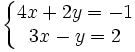 .
.La première équation équivaut à
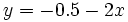 (voir plus haut).
(voir plus haut).La deuxième équation équivaut à :
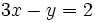 ;
;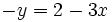 ;
;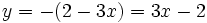 .
.
En traçant les droites d'équations respectives
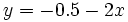 et
et 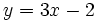 , on voit que leur point d' intersection est
, on voit que leur point d' intersection est 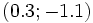 .La solution (approximative) du système est
.La solution (approximative) du système est 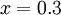 et
et 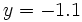 .
.Résolution algébrique
Il existe deux méthodes a priori différentes, mais qui reposent sur le même principe de base : élimination d'une inconnue. Détaillons-les sur un exemple.
Méthode par substitution
Exemple : Reprenons le système :
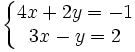 .
.Exprimons
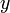 en fonction de
en fonction de  dans la première équation. On obtient
dans la première équation. On obtient 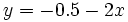 . Remplaçons donc
. Remplaçons donc 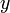 par
par 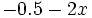 dans la deuxième équation. On a :
dans la deuxième équation. On a :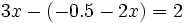 ;
;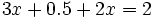 ;
;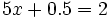 ;
;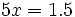 ;
;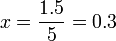 .
.
Or,
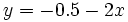 . Donc on obtient :
. Donc on obtient : 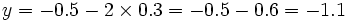 .
.La solution du système est le couple
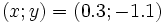 .
.Méthode par combinaison ou élimination
Cette méthode est aussi appelée "méthode par addition" ou "par combinaison linéaire".
Exemple : Reprenons le système :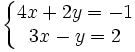 .
.Pour éliminer
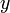 , multiplions la deuxième ligne par
, multiplions la deuxième ligne par 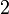 et additionnons les deux lignes ainsi obtenues. On a :
et additionnons les deux lignes ainsi obtenues. On a : 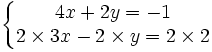 puis
puis 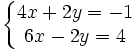 et l'addition donne :
et l'addition donne : 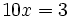
. En résolvant cette équation, on obtient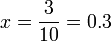 .
.Remplaçons
 par
par 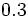 dans la première ligne. On obtient :
dans la première ligne. On obtient :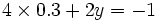 ;
;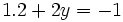 ;
;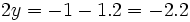 ;
;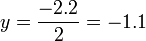 .
.
On retrouve la solution
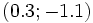
Cas général
D'une manière générale, pour un système sous la forme :
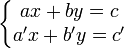 , pour lequel le déterminant
, pour lequel le déterminant 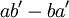 est non nul, on a
est non nul, on a 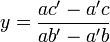 et
et 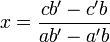 .Démonstration
.Démonstration
Le déterminant étant non nul, l'un au moins des coefficients a ou b est non nul. On peut, sans perdre de généralité, supposer que a est non nul. Sinon, on effectue un raisonnement analogue en divisant par b.On a :
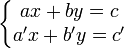
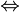
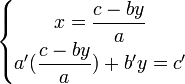 .
.
La première équation est donc :
Et la seconde équation donne :
- a'(c − by) + ab'y = ac' (en multipliant par a)
- a'c − a'by + ab'y = ac'
- y(ab' − a'b) = ac' − a'c
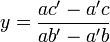
La première équation s'écrit alors :
Système de 3 équations à 3 inconnues
Les systèmes de 3 équations à 3 inconnues se résolvent aussi de cette manière :
Méthode par substitution
![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ 2x-y+2z=2 \quad[2] \\ -x+y+z=-3 \quad[3] \end{matrix}\right.](/pictures/frwiki/99/c5839baae05cad180709721d5624bd51.png) .
.
Pour résoudre ce système de 3 équations à 3 inconnues, on isole une inconnue dans une des équations. Dans ce système, on isole l'inconnue x dans l'équation [1]
- [1] :
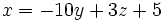 .
.
Maintenant on remplace l'inconnue
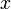 dans les équations [2] et [3], qui donne un système de 2 équations à 2 inconnues à résoudre avec les méthodes de substitution ou d'addition .
dans les équations [2] et [3], qui donne un système de 2 équations à 2 inconnues à résoudre avec les méthodes de substitution ou d'addition .![\left\{\begin{matrix} 2(-10y+3z+5)-y+2z=2 [2] \\ -(-10y+3z+5)+y+z=-3 [3] \end{matrix}\right.](/pictures/frwiki/48/0d72ef1c3af9f1d19f024a856fd583ca.png) .
.
Après avoir trouvé
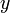 et
et 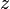 , on les remplace dans l'équation [1] pour trouver
, on les remplace dans l'équation [1] pour trouver 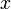 .
.Méthode par élimination
![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ 2x-y+2z=2 \quad[2] \\ -x+y+z=-3 \quad[3] \end{matrix}\right.](/pictures/frwiki/99/c5839baae05cad180709721d5624bd51.png) .
.
Pour résoudre ce système, on peut éliminer
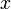 par exemple dans les équations [2] et [3] en les remplaçant par les équations - 2 × [1] + [2] et [1] + [3]. Le système est alors équivalent au système
par exemple dans les équations [2] et [3] en les remplaçant par les équations - 2 × [1] + [2] et [1] + [3]. Le système est alors équivalent au système![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ -21y+8z=-8 \quad[2'] \\ 11y-2z=2\quad[3'] \end{matrix}\right.](/pictures/frwiki/57/98a63d59963034ea69dff064a268236c.png) .
.
Il suffit alors d'éliminer une autre inconnue,
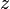 par exemple, dans [3'] en la remplaçant par 4 × [3'] + [2']. Le système est alors équivalent au système triangulaire suivant :
par exemple, dans [3'] en la remplaçant par 4 × [3'] + [2']. Le système est alors équivalent au système triangulaire suivant :L'équation [3"] permet de trouver
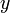 , qui remplacé dans l'équation [2'] permet de trouver
, qui remplacé dans l'équation [2'] permet de trouver 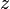 . Ces deux valeurs, remplacées dans l'équation [1] permet de trouver
. Ces deux valeurs, remplacées dans l'équation [1] permet de trouver 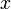
Cette méthode se généralise à des systèmes comportant davantage d'équations et davantage d'inconnues et prend le nom de méthode du pivot de Gauss.
Voir aussi
Article connexe
- Système d'équations linéaires, article plus avancé sur le sujet
- Portail des mathématiques
Catégories : Mathématiques élémentaires | Équation
Wikimedia Foundation. 2010.

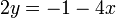
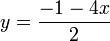
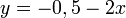
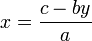
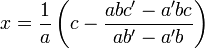
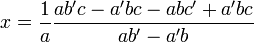
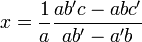
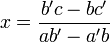
![\left\{\begin{matrix} x+10y-3z=5 \quad[1] \\ -21y+8z=-8 \quad[2'] \\ 23y=0\quad[3''] \end{matrix}\right.](/pictures/frwiki/53/52de18b453467277e7d3f3c9a91552e4.png)