Operations sur les derivees

Operations sur les derivees

Opérations sur les dérivées

Icone math élém.jpg
Cet article fait partie de la série
Mathématiques élémentaires
Algèbre
Logique
Arithmétique
Probabilités
Statistiques

Le calcul de la dérivée de certaines fonctions à valeurs réelles ou complexes (ou plus généralement dans un corps topologique) peut être effectué en utilisant un certain nombre d'opérations sur les dérivées, notamment certaines liées aux opérations sur les nombres réels et complexes. Les démonstrations de ces propriétés découlent des opérations sur les limites.

Dans tout l'article, on note f et g deux fonctions qu'on suppose dérivables.

Sommaire

Linéarité

La dérivation est un opérateur linéaire, c'est-à-dire que l'espace des fonctions dérivables est stable par somme et par multiplication de ses éléments par des réels (c'est un espace vectoriel réel), et les relations suivantes sont vérifiées :

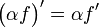
\bigl(\alpha f\bigr)'=\alpha f'
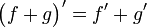
\bigl(f+g\bigr)' = f'+g'
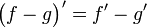
\bigl(f-g\bigr)' = f'-g'

Composition

La composition de deux fonctions dérivables est dérivable, là où elle est définie (précisément sur l'image réciproque par f du domaine de définition de g) et se calcule suivant la règle :

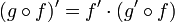(g \circ f)' = f' \cdot (g' \circ f).

Cette règle admet pour conséquence la règle de calcul de l'inverse d'une fonction (on se place sur un intervalle sur lequel f ne s'annule pas), en utilisant le calcul élémentaire de la dérivée de la fonction x\mapsto \tfrac1x :

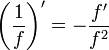
\left( \dfrac{1}{f} \right)' = -\dfrac{f'}{f^2}

Produit et quotient

Article détaillé : règle du produit.

La dérivation est un opérateur différentiel, c'est-à-dire que l'espace des fonctions dérivables est stable par multiplication, et la formule de Leibniz est vérifiée :

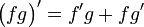\bigl(fg\bigr)' = f'g + fg'.
Démonstration

On montre la relation en un point x0 appartenant aux domaines de dérivabilité de f et de g. Le taux de variation de fg s'écrit en ce point :

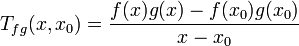T_{fg}(x,x_0) = \dfrac{f(x)g(x)-f(x_0)g(x_0)}{x-x_0}.

À titre d'artifice de calcul, introduisons le terme neutre − f(x)g(x0) + g(x0)f(x) :

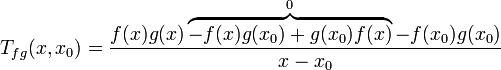T_{fg}(x,x_0) = \dfrac{f(x)g(x) \overbrace{- f(x)g(x_0) + g(x_0)f(x)}^0 - f(x_0)g(x_0)}{x-x_0}.

En factorisant les termes, on reconnaît les taux de variation de f et g :

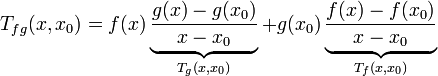T_{fg}(x,x_0) = f(x) \underbrace{\dfrac{g(x) - g(x_0)}{x-x_0}}_{T_g(x, x_0)} + g(x_0) \underbrace{\dfrac{f(x) - f(x_0)}{x-x_0}}_{T_f(x, x_0)}.

En passant à la limite, et sachant que la dérivabilité implique la continuité, les trois relations suivantes sont vraies :

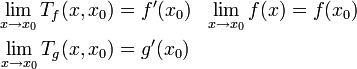\begin{align} \lim_{x\to x_0} T_{f}(x,x_0) &= f'(x_0) & \lim_{x\to x_0} f(x) &= f(x_0) \\ \lim_{x\to x_0} T_{g}(x,x_0) &= g'(x_0) \end{align}.

Enfin, sachant que la limite d'un produit est égale au produit des limites :

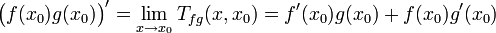\bigl(f(x_0)g(x_0)\bigr)' = \lim_{x\to x_0} T_{fg}(x,x_0) = f'(x_0)g(x_0) + f(x_0)g'(x_0).

Cette relation valable en tout tel point x0 montre la relation attendue entre les fonctions.

En particulier, cette relation admet comme conséquences la règle de dérivation des puissances :

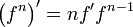\bigl(f^n\bigr)' = nf'f^{n-1},

et celle pour la dérivée d'un quotient :

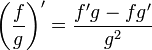
\left( \dfrac{f}{g} \right)' = \dfrac{f'g-fg'}{g^2}

Fonction réciproque

Soit f une fonction dérivable et strictement monotone de l'intervalle I sur l'intervalle J = f(I). Si f' ne s'annule par sur I alors la fonction f − 1 est dérivable sur J et

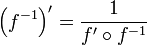\left(f^{-1}\right)' = \frac{1}{f' \circ f^{-1}}.
Démonstration

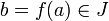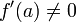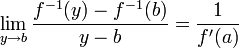On souhaite prouver que f − 1 est dérivable en b = f(a)\in J. En supposant f'(a) \ne 0 , montrons que \lim_{y \to b}{\frac{f^{-1}(y) - f^{-1}(b)}{y - b}} = {1 \over {f'(a)}}.

La fonction f étant dérivable en a, on a

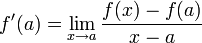f'(a) = \lim_{x \to a}{\frac{f(x)-f(a)}{x-a}}.

Comme f − 1 est continue en b, le théorème de composition des limites donne

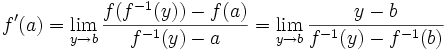f'(a) = \lim_{y \to b}{\frac{f(f^{-1}(y)) - f(a)}{f^{-1}(y) - a}} = \lim_{y \to b}{\frac{y-b}{f^{-1}(y) - f^{-1}(b)}}.

Cette limite étant non nulle, d'après le théorème sur l'inverse d'une limite, on a

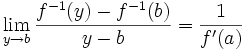
\lim_{y \to b}{\frac{f^{-1}(y) - f^{-1}(b)}{y-b}} ={ 1 \over f'(a)}
ou encore
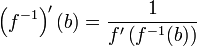\left(f^{-1}\right)'(b) =\frac{1}{f'\left(f^{-1}(b)\right)}.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Op%C3%A9rations sur les d%C3%A9riv%C3%A9es ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Operations sur les derivees de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Opérations sur les dérivées — Le calcul de la dérivée de certaines fonctions à valeurs réelles ou complexes (ou plus généralement dans un corps topologique) peut être effectué en utilisant un certain nombre d opérations sur les dérivées, notamment certaines liées aux… …   Wikipédia en Français

  • Opérations sur les limites — Cette page est une annexe de l article limite (mathématiques élémentaires), qui explique comment traduire en termes de limites les opérations usuelles : addition, multiplication, composition... Tous les résultats listés ici sont valables à… …   Wikipédia en Français

  • Derivees usuelles — Dérivées usuelles Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Dérivées Usuelles — Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Dérivées — Dérivée  Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… …   Wikipédia en Français

  • Dérivées usuelles — Cet article énumère les fonctions dérivées de la plupart des fonctions usuelles. Domaine de définition Fonction Domaine de dérivabilité Dérivée Condition ou remarque …   Wikipédia en Français

  • DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) — LES ÉQUATIONS aux dérivées partielles sont sans doute le domaine des mathématiques où le lien avec la physique est le plus étroit. Il ne s’agit pas seulement du fait que les recherches les plus actives, et en général les plus importantes, ont été …   Encyclopédie Universelle

  • Distance entre deux points sur le plan cartésien — Dans le plan cartésien, les points sont définis à l aide de leurs coordonnées dites cartésiennes. Soit deux points A et B dans le plan cartésien. On appelle (xA,yA) les coordonnées du point A et (xB,yB) les coordonnées du point B : alors la… …   Wikipédia en Français

  • Les droits de l'homme en Iran — Droits de l homme en Iran À partir du XIXe siècle la notion de droits de l homme commence à pénétrer en Iran. Au cours du XXe siècle, les droits de l homme font l objet de luttes pour leur application et de restrictions diverses, qui… …   Wikipédia en Français

  • Les statistiques et la sociologie — Statistiques  Pour un article sur une statistique consultez l article statistique La statistique est à la fois une science d un point de vue théorique, une méthode et une technique. Elle comprend la collecte, l analyse, l interprétation de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”