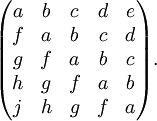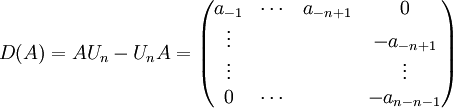- Matrice de toeplitz
-
Matrice de Toeplitz
En algèbre linéaire, une matrice de Toeplitz (d'après Otto Toeplitz) ou matrice à diagonales constantes est une matrice dont les coefficients sur une diagonale descendant de gauche à droite sont les mêmes. Par exemple, la matrice suivante est une matrice de Toeplitz :
Toute matrice A à m lignes et n colonnes de la forme
est une matrice de Toeplitz. Si l'élément situé à l’intersection des ligne i et colonne j de A est noté Ai,j, alors on a :
- Ai,j = ai − j.
Sommaire
Propriétés
En général, une équation matricielle
- Ax = b
correspond à un système de n équations linéaires à résoudre. Si A est une matrice de Toeplitz, alors le système est particulier : il ne contient que 2n − 1 informations arrangées d'une manière bien particulière au lieu de n2 dans le cas général.
Cette propriété peut être établie en observant la matrice :
- AUn − UnA,.
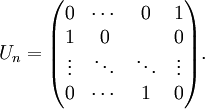
Ici Un est donnée par
Si on effectue la multiplication de Un par un vecteur v, cela décale tous les coefficients de v d'une ligne vers le bas, et le dernier coefficient monte à la première ligne.
Un calcul simple donne
où les cases vides peuvent être remplacées par des zéros. On voit qu'elle est de rang au plus 2. On dira que D(A) est la matrice de déplacement de A.
Si A est inversible et de Toeplitz, son inverse n'est pas de Toeplitz, sauf si A est triangulaire. Néanmoins, l'inverse de A a quand même une propriété intéressante : si on multiplie D(A) par l'inverse de A, on obtient − D(A − 1), qui est donc aussi de rang au plus 2.
Pour cette raison, si A est une matrice telle que AUn − UnA, soit de rang r, on dira qu'elle est de type Toeplitz, de rang de déplacement r[1].
Calcul avec des matrices de Toeplitz
Ces matrices sont très intéressantes du point de vue de la complexité du calcul : on montre que l'addition de deux matrices de Toeplitz peut être effectuée en O(n) opérations et le produit matriciel de deux matrices de Toeplitz en O(n log n) opérations.
La résolution de systèmes linéaires dont la matrice est de Toeplitz peut être rendue très rapide -- typiquement en O(nlog(n)2) opérations, au moyen de la conjonction de plusieurs procédés algorithmiques. Ces procédés s'étendent aux matrices de type Toeplitz, et ils sont intéressants pour une matrice de rang de déplacement r petit devant n, car ils fournissent des algorithmes en O(nr2log(n)2) opérations, à comparer avec O(n3) opérations pour une matrice pleine quelconque[2].
Cependant, une matrice de Toeplitz peut être fort mal conditionnée, et donc la solution obtenue avec une erreur relative forte si on calcule en nombres flottants, ou avec des fractions gigantesques, si on calcule exactement en rationnels[3].
Ces matrices sont aussi étroitement liées aux séries de Fourier car l'opérateur multiplication par un polynôme trigonométrique, comprimé (restreint) à un espace de dimension finie, peut être représentée par une telle matrice.
Si une matrice de Toeplitz vérifie de plus ai = ai + n, alors c'est une matrice circulante.
Annexes
Notes et références
- ↑ (en) Polynomial and matrix computations. Vol. 1,Dario Bini et Victor Pan, Birkhäuser Boston Inc., Boston, MA, 1994.
- ↑ (en) Algebraic methods for Toeplitz-like matrices and operators, Georg Heinig et Karla Rost, Birkhäuser Verlag, Bâle, 1984.
- ↑ (en) Introduction to large truncated Toeplitz matrices, Albrecht Böttcher et Bernd Silbermann, Springer-Verlag, New York, 1999.
Lien externe
- Portail des mathématiques
Catégorie : Matrice remarquable
Wikimedia Foundation. 2010.