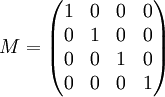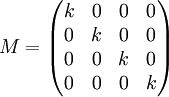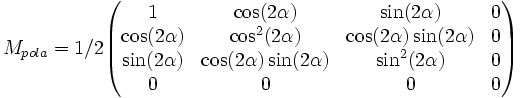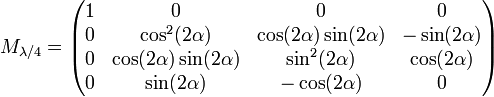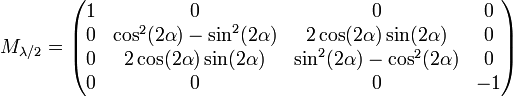Matrice de Muller

Matrice de Muller

Matrice de Mueller

La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs qui représentent la polarisation de la lumière incohérente.


Sommaire

Matrice de Muller

Pour chaque composant optique, on trouve une matrice de Mueller.

Région isotrope, non absorbante

  • Région vide, ou isotrope et non absorbante :
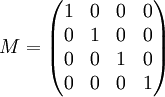
M=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix}

Région isotrope, absorbante

  • Région isotrope avec un coefficient d'absorption 1-k (0<k<1) :
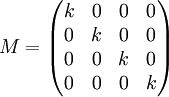
M=\begin{pmatrix} k & 0 & 0 & 0\\ 0 & k & 0 & 0\\ 0 & 0 & k & 0\\ 0 & 0 & 0 & k\\ \end{pmatrix}

Polariseur linéaire

  • Polariseur linéaire avec un angle de transmission α :
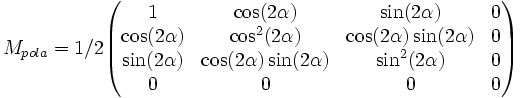
M_{pola}=1/2\begin{pmatrix} 1 & \cos(2\alpha) & \sin(2\alpha) & 0\\ \cos(2\alpha) & \cos^{2}(2\alpha) & \cos(2\alpha)\sin(2\alpha) & 0\\ \sin(2\alpha) & \cos(2\alpha)\sin(2\alpha) & \sin^{2}(2\alpha) & 0\\ 0 & 0 & 0 & 0\\ \end{pmatrix}

Lame de retard

  • Lame de retard quart-d'onde avec azimut α pour l'axe rapide :
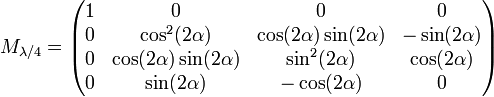
M_{\lambda/4}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & \cos^{2}(2\alpha) & \cos(2\alpha)\sin(2\alpha) & -\sin(2\alpha)\\ 0 & \cos(2\alpha)\sin(2\alpha) & \sin^{2}(2\alpha) & \cos(2\alpha)\\ 0 & \sin(2\alpha) & -\cos(2\alpha) & 0\\ \end{pmatrix}
  • Lame de retard demi-onde avec azimut α pour l'axe rapide :
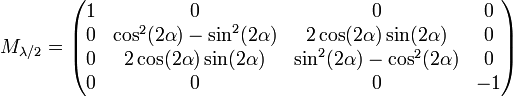
M_{\lambda/2}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & \cos^{2}(2\alpha)- \sin^{2}(2\alpha) & 2\cos(2\alpha)\sin(2\alpha) & 0\\ 0 & 2\cos(2\alpha)\sin(2\alpha) & \sin^{2}(2\alpha)-\cos^{2}(2\alpha) & 0\\ 0 & 0 & 0 & -1\\ \end{pmatrix}
  • Lame de retard δ avec azimut α pour l'axe rapide :
Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Matrice de Mueller ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice de Muller de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Matrice De Mueller — La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs qui représentent la polarisation de la lumière incohérente. Sommaire 1 Matrice de Muller 1.1 Région… …   Wikipédia en Français

  • Matrice de mueller — La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs qui représentent la polarisation de la lumière incohérente. Sommaire 1 Matrice de Muller 1.1 Région… …   Wikipédia en Français

  • Matrice De Hadamard — Une matrice de Hadamard, du nom du mathématicien français Jacques Hadamard, est une matrice carrée dont les coefficients sont tous 1 ou 1 et dont les lignes sont toutes orthogonales entre elles. Le nom retenu pour ces matrices rend hommage au… …   Wikipédia en Français

  • Matrice de hadamard — Une matrice de Hadamard, du nom du mathématicien français Jacques Hadamard, est une matrice carrée dont les coefficients sont tous 1 ou 1 et dont les lignes sont toutes orthogonales entre elles. Le nom retenu pour ces matrices rend hommage au… …   Wikipédia en Français

  • Muller — Müller Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronyme 1.1 Muller 1.2 Nom composé …   Wikipédia en Français

  • Matrice de Hadamard — Une matrice de Hadamard est une matrice carrée dont les coefficients sont tous 1 ou 1 et dont les lignes sont toutes orthogonales entre elles. Le nom retenu pour ces matrices rend hommage au mathématicien français Jacques Hadamard, même si les… …   Wikipédia en Français

  • Müller — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T …   Wikipédia en Français

  • Alfredo Müller — dans son atelier à Paris (73, rue Coulaincourt) en 1908 …   Wikipédia en Français

  • Code De Reed-Müller — Les codes de Reed Müller sont des codes correcteurs linéaires. Cette famille de codes, initialement binaire, doit son nom aux travaux de D.E. Muller qui proposa le principe du code et à Irving S. Reed qui proposa une technique de décodage,… …   Wikipédia en Français

  • Code de Reed-Muller — Code de Reed Müller Les codes de Reed Müller sont des codes correcteurs linéaires. Cette famille de codes, initialement binaire, doit son nom aux travaux de D.E. Muller qui proposa le principe du code et à Irving S. Reed qui proposa une technique …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”