Chaos Quantique

Chaos Quantique

Chaos quantique

Le « chaos quantique » est un raccourci qui désigne un champ de recherches ouvert dans les années 1970 qui est issu des succès de la théorie du chaos en dynamique hamiltonienne classique. Ce champ de recherche tente essentiellement de répondre à la question :

Quel est le comportement en mécanique quantique d'un système classiquement chaotique ?


Ces recherches ont montré que :

  • il n'existe pas de « chaos quantique » au sens strict du terme, c'est-à-dire qu'il n'existe pas de divergence exponentielle des états quantiques au cours du temps dans l'espace de Hilbert qui serait l'analogue de la divergence exponentielle des orbites dans l'espace des phases classique. Cette absence de « sensibilité aux conditions initiales » en mécanique quantique est lié au fait que l'équation de Schrödinger est une équation linéaire. C'est pourquoi Michael Berry a suggeré d'utiliser l'expression « chaologie quantique » à la place de « chaos quantique ».
  • cependant, les systèmes physiques classiquement chaotiques présentent certaines propriétés quantiques clairement distinctes de celles des systèmes classiquement intégrables : il existe en quelque sorte des « signatures » quantiques du chaos classique sous-jacent.

Sommaire

Signatures quantique du chaos classique

Orbites périodiques & spectre d'énergie

En utilisant la formulation de Feynman en intégrale de chemin de la mécanique quantique, Martin Gutzwiller (IBM, New York) a démontré en 1971 une relation intégrale liant à la limite semi-classique le spectre d'énergie quantique d'un système physique aux orbites périodiques classiques de ce même système. Cette relation est aujourd'hui appelée formule des traces de Gutzwiller en son honneur[1]. Or, les orbites périodiques ont des propriétés très différentes selon que la dynamique hamiltonienne classique est intégrable ou chaotique.

Il est intéressant de remarquer qu'il existe un système physique pour lequel la formule des traces approchée de Gutzwiller est en fait exacte : c'est le flot géodésique sur une surface compacte à courbure négative constante[2] . Une telle surface X peut se représenter comme l'espace quotient du demi-plan de Poincaré 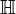\mathbb{H} par un sous-groupe discret Γ du groupe 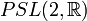PSL(2,\mathbb{R}) des isométries :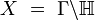

X \ = \ \Gamma \backslash \mathbb{H}

Cette formule exacte a été établie en 1956 par le mathématicien Selberg (indépendamment de la physique et des intégrales de chemin), et est aujourd'hui appelée formule des traces de Selberg en son honneur.

Propriétés statistiques du spectre d'énergie

Les propriétés statistiques du spectre d'énergie d'un système physique classiquement chaotique sont très différentes de celle d'un système intégrable. Oriol Bohigas, Marie-Joya Giannoni et Charles Schmidt (Institut de physique nucléaire, Orsay) ont conjecturé que les propriétés des fluctuations statistiques du spectre d'énergie d'un système physique classiquement chaotique sont universelles (une fois normalisées), et bien décrites par un ensemble de matrices aléatoires qui ne dépend que des symétries du système.

Cicatrices (scars)

Articles liés

Bibliographie

Généralités

  • Martin C. Gutzwiller ; Quantum Chaos, Scientific American (January 1992).
  • Marie-Joya Giannoni, André Voros & Jean Zinn-Justin (éditeurs) ; Chaos & Quantum Physics, proceeedings de l'École d'Eté de Physique Théorique des Houches, Session 52 (1989), North-Holland (1991), ISBN 0-444-89277-X.
  • Martin C. Gutzwiller ; Chaos in classical & quantum mechanics, Interdisciplinary Applied Mathematics 1, Springer-Verlag (1990), ISBN 0-387-97173-4.
  • Michael V. Berry ; Quantum chaology (The Bakerian Lecture), Proceedings of the Royal Society A 413 (1987) 183-198. Texte complet disponible au format pdf.
  • Michael V. Berry ; Quantum chaology, not quantum chaos, Physica Scripta 40 (1989) 335-336. Texte complet disponible au format pdf.
  • Michael V. Berry ; Chaology ; the emerging science of unpredictability, Proceedings of the Royal Institution of Gt Britain, 61 (1990) 189-204. Texte complet disponible au format pdf.

Formule des traces de Gutzwiller

  • Martin Lubcke ; Gutzwiller Trace Formula and Applications (Juin 2001). Texte au format pdf.

Optique atomique

  • Farhan Saif ; Classical and Quantum Chaos in Atom Optics, Physics Reports 419 (2005) 207 et Physics Reports 425 (2006) 369. Texte complet disponible sur l'ArXiv : quant-ph/0604066.

Notes & références

  1. ↑ Martin C. Gutzwiller ; Periodic orbits and classical quantization conditions, Journal of Mathematical Physics 12 no. 3 (1971).
  2. ↑ Nandor Balàzs & André Voros ; Chaos on the pseudosphere, Physics Report 143 (1986) 109.
  • Portail de la physique Portail de la physique
Ce document provient de « Chaos quantique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Chaos Quantique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Chaos quantique — Le « chaos quantique » est un raccourci qui désigne un champ de recherches ouvert dans les années 1970 qui est issu des succès de la théorie du chaos en dynamique hamiltonienne classique. Ce champ de recherche tente essentiellement de… …   Wikipédia en Français

  • Theorie du chaos — Théorie du chaos Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des sys …   Wikipédia en Français

  • Théorie du Chaos — Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des sys …   Wikipédia en Français

  • Théorie du chaos — Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des systèmes dynamiques rigoureusement déterminis …   Wikipédia en Français

  • Fonction Zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction Zêta De Riemann — En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des nombres premiers. Elle est… …   Wikipédia en Français

  • Fonction dzêta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction zéta — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction zêta de Riemann — La fonction zêta de Riemann ζ(s) dans le plan complexe. La couleur d un point s code la valeur de ζ(s) : des couleurs vives indiquent des valeurs proches de 0 et la nuance indique l argument de la valeur. Le point blanc pour s = 1… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”