Loi de Cauchy

Loi de Cauchy
Page d'aide sur l'homonymie Pour les articles homonymes, voir Cauchy.
Page d'aide sur l'homonymie Ne pas confondre avec la loi de Cauchy en optique.
Cauchy
Densité de probabilité / Fonction de masse
Densité de la loi de Cauchy, pour différentes valeurs de x0 et a
Fonction de répartition
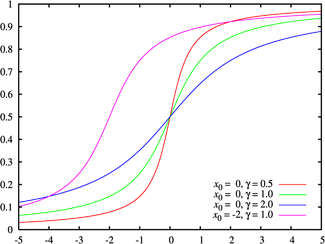
Fonction de répartition pour la loi de Cauchy
Les couleurs correspondent au graphe préécédent
Paramètres x_0\! Paramètre de location (réel)
a > 0\! Paramètre d'échelle (réel)
Support x \in (-\infty; +\infty)\!
Densité de probabilité (fonction de masse) \frac{1}{\pi a\,\left[1 + \left(\frac{x-x_0}{a}\right)^2\right]} \!
Fonction de répartition \frac{1}{\pi} \arctan\left(\frac{x-x_0}{a}\right)+\frac{1}{2}
Espérance non définie
Médiane (centre) x0
Mode x0
Variance non définie
Asymétrie non définie
Kurtosis normalisé non définie
Entropie \ln(4\,\pi\,a)\!
Fonction génératrice des moments non définie
Fonction caractéristique \exp(x_0\,i\,t-a\,|t|)\!
modifier Consultez la documentation du modèle

La loi de Cauchy, appelée aussi loi de Lorentz, est une loi de probabilité classique qui doit son nom au mathématicien Augustin Louis Cauchy.

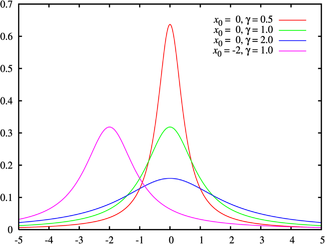
Une variable aléatoire X suit une loi de Cauchy si elle admet une densité fX par rapport à la mesure de Lebesgue, dépendant des deux paramètres x0 et a (a > 0) et définie par :

\begin{align} f(x; x_0,a) &= \frac{1}{\pi a \left[1 + \left(\frac{x-x_0}{a}\right)^2\right]} \\[0.5em] &= { 1 \over \pi } \left[ { a \over (x - x_0)^2 + a^2 } \right] \end{align}

Cette distribution est symétrique par rapport à x0 (Paramètre de location), le paramètre a donnant une information sur l'étalement de la fonction (Paramètre d'échelle).

L'inverse d'une variable aléatoire, de loi de Cauchy, suit une loi de Cauchy.

Le quotient de deux variables aléatoires réelles indépendantes suivant des lois normales standards suit une loi de Cauchy.

Espérance et écart type

La loi de Cauchy n'admet ni espérance ni écart type. Et il en va de même pour tout moment d'ordre supérieur. En effet,

x \mapsto \frac{a}{\pi}\frac{x}{(x-x_0)^2+a^2}\, n'est pas intégrable au sens de Lebesgue

car \left|\frac{x}{(x-x_0)^2+a^2}\right| \sim \left|\frac{1}{x}\right| (à l'infini) d'où la divergence de l'intégrale : l'espérance n'existe pas.

A fortiori, la loi de Cauchy n'admet pas d'écart-type ( \int_{-\infty}^{+\infty} \frac{a}{\pi}\frac{x^2}{(x-x_0)^2+a^2}\, \mathrm{d}x diverge). Pour la même raison, les moments d'ordre supérieur n'existent pas non plus.

Cependant, x0, qui en est la médiane, est souvent considéré comme la « moyenne » de la loi de Cauchy, car :

\lim_{R \rightarrow + \infty} \int_{-R}^R \frac{a}{\pi}\frac{x}{(x-x_0)^2+a^2}\, \mathrm{d}x = x_0

Loi de Cauchy et théorèmes limite

Moyenne empirique d'une série de valeurs suivant la loi de Cauchy.

La loi de Cauchy est l'une de celles auxquelles la Loi des grands nombres ne s'applique pas: partant d'un échantillon d'observations x_1, x_2, \cdots, x_n issues d'une loi de Cauchy, la moyenne empirique

\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i

ne converge pas vers une quantité déterministe (à savoir l'espérance de la loi). Au contraire, cette moyenne reste aléatoire: elle est elle-même distribuée selon une loi de Cauchy.

Elle nous montre ainsi que la condition de l'espérance définie selon l'intégrale de Lebesgue est indispensable à l'application de la loi. On remarque que les valeurs moyennes s'approchent de x0 mais il arrive toujours un moment où une valeur trop éloignée « empêche » la moyenne de converger. La probabilité d'obtenir des valeurs éloignées de x0 est en fait trop élevée pour permettre à la moyenne empirique de converger.

v · Lois de probabilités
Lois discrètes
à support fini Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique
Lois continues
à support compact Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel
v · Augustin Louis Cauchy
Règle de Cauchy • Produit de Cauchy • Critère de Cauchy • Théorème de Cauchy-Lipschitz • Équations de Cauchy-Riemann • Inégalité de Cauchy • Théorème de Cauchy • Loi de Cauchy • Formule de Binet-Cauchy
Théorème de la moyenne de Cauchy • Théorème de Cauchy-Kovalevskaïa • Théorème intégral de Cauchy • Inégalité de Cauchy-Schwarz • Formule intégrale de Cauchy
  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Cauchy de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Loi De Cauchy — Pour les articles homonymes, voir Cauchy. Cauchy Densité de probabilité / Fonction de masse …   Wikipédia en Français

  • Loi de cauchy — Pour les articles homonymes, voir Cauchy. Cauchy Densité de probabilité / Fonction de masse …   Wikipédia en Français

  • Loi de Cauchy (optique) —  Ne pas confondre avec la loi de Cauchy en probabilité. Illustration de la loi de Cauchy sur l exemple d un verre borosilicate …   Wikipédia en Français

  • Loi De Probabilité — Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement étendu le concept… …   Wikipédia en Français

  • Loi de probabilite — Loi de probabilité Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement …   Wikipédia en Français

  • Loi De Student — Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi de student — Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 …   Wikipédia en Français

  • Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”