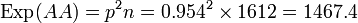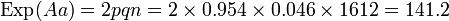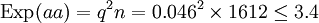Loi de Castle-Hardy-Weinberg

Principe de Hardy-Weinberg

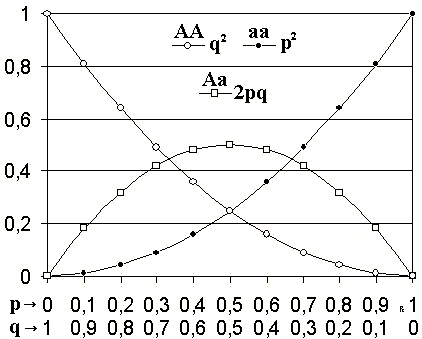Le principe de Hardy-Weinberg pour deux allèles : l'axe horizontal indique les deux fréquences d'allèle p et q, l'axe vertical indique la fréquence des génotypes et les trois génotypes possibles sont représentés par des glyphes différents

Le principe de (Castle-)Hardy-Weinberg ou la loi ou le modèle du même nom est une théorie qui postule qu'il y a un équilibre de la fréquence des allèles et des génotypes au cours des générations.

Sommaire

1 Hypothèses de départ
2 Loi de distribution génotypique
3 Causes de déviation
4 Généralisations
- 4.1 Généralisation en cas de polyploïdie
- 4.2 Généralisation complète
5 Applications
6 Histoire
7 Source

Hypothèses de départ

Pour que l'équilibre existe, plusieurs hypothèses sont décrites :

La population est de taille infinie (~ grande taille, loi des grands nombres)
Espèces diploïde et reproduction sexuée

La Panmixie (croisements aléatoires entre individus) généralisée recouvre :
- Équiprobabilité des gamètes : pangamie
- Rencontre des gamètes au hasard ou formation aléatoire des couples ((Panmixie))**Ségrégation aléatoire des gamètes lors de la méïose

Absence de migration
Absence de mutation sur les allèles considérés
Absence de sélection d'individus

Les générations ne se chevauchent pas

Il faut cependant distinguer l'équilibre de (Castle-)Hardy-Weinberg de la structure de (Castle-)Hardy-Weinberg qui ne concerne pas la transmission des allèles d'une génération à une autre mais la relation entre fréquences alléliques et distribution des génotypes.

Loi de distribution génotypique

De cet équilibre de Hardy-Weinberg, découle la loi de distribution génotypique :

p² + q² + 2 pq = 1

Soit A et a, deux allèles de fréquence respectivement p et q.

Avec :

p² :la fréquence d'un génotype homozygote AA pour deux alléles "A/"
q² : la fréquence d'un génotype homozygote aa pour deux allèles "a/"
2pq : la fréquence d'un génotype hétérozygote Aa pour un allèle "A/" et un allèle "a/"

La loi d'Hardy-Weinberg est :

Dans une population isolée d'effectif illimité, non soumise à la sélection, et dans laquelle il n'y a pas de mutations, les fréquences alléliques restent constantes.
Si les accouplements sont panmictiques, les fréquences génotypiques se déduisent directement des fréquences alléliques et restent également constantes.

Cette loi décrit la structure génétique de nombreuses populations pour lesquelles les hypothèses de départ ne sont pas prospectées.

Causes de déviation

Quand les hypothèses du principe de Hardy-Weinberg ne sont pas réunies, ceci peut causer une déviation significative, c'est à dire que les fréquences génotypiques observées seront différentes des attendus théoriques. Les déviations observées peuvent être dues à un effet Wahlund, de la dépression de consanguinité, de la sélection pré-zygotique ou de la sélection post-zygotique ou enfin par dérive génétique.

Généralisations

Généralisation en cas de polyploïdie

Généralisation complète

Applications

Calcul de fréquences géniques

Le calcul est simple lorsque les gènes sont codominants, il suffit de les compter à partir des phénotypes observés, dont le génotype est certain, et nous obtenons immédiatement une estimation des fréquences géniques.

Lorsque nous avons un ou des gènes récessifs, nous devons tenir compte des divers génotypes possibles.

Il en est ainsi du système de groupe sanguin ABO que nous prenons (d'après R.R. Race et R. Sanger, Les groupes sanguins chez l'homme, Masson 1970) pour exemple de calcul.

Le système ABO comporte 3 allèles, A, B, et O, ce dernier étant récessif. Par souci de simplification, nous ne différencions pas les 2 allèles A1 et A2 qui déterminent deux sortes différentes de groupe A, A1 étant dominant sur A2. Nous observons donc 4 phénotypes possibles. Nous observons, d'après M. goudemand et Ch. Salmon, les fréquences suivantes en France, arrondies à trois décimales :

A , fréquence 0.437, génotypes possibles A/A, A/O

B , fréquence 0.092, génotypes possibles B/B, B/O

AB, fréquence 0.036, génotype certain A/B

O , fréquence 0.435, génotype certain O/O

Soit a, b, o les fréquences géniques respectives des allèles A, B, O. Nous avons, par définition, a + b + o = 1

La fréquence du génotype O/O, égale à o² étant de 0.435, nous en déduisons la fréquence génique de o, soit : o = 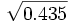$\sqrt {0.435}$ = 0.6595

La fréquence génique de l'allèle A en découle, car nous avons la fréquence des sujets A = 0.437 = a² + 2ao = a² + 1.3190a d'où a = 0.2743

La valeur de b s'en déduit immédiatement ; b =1 -(0.6595 + 0.2743)= 0.0662

Ou plus simplement la méthode de Bernstein :

o = 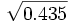$\sqrt {0.435}$ = 0.6595

b = 1 - (a + o) = 1 - 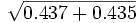$\sqrt {0.437+0.435}$ = 1 - 0.9338 = soit b = 0.0662

a = 1- (b + o) = 1 - 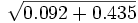$\sqrt {0.092+0.435}$ = 1 - 0.7259, soit a = 0.2741

Le total o+a+b n'est pas égal exactement à 1, et certaines corrections doivent être apportées, et l'ont été tant par Bernstein, qu'ultérieurement par d'autres auteurs -Taylor et Prior (1938), R.A. Fisher et G.L. Taylor (1940), A.M. Dobson et E.W. Ikin (1946) et J.A.F. Roberts (1948) en ont publié les formules d'application.

Tests de signification pour la déviation

L'écart par rapport à la loi de Hardy-Weinberg est estimé grâce au Test du χ² de Pearson, en comparant la structure des fréquences génotypiques obtenues à partir des données observées, aux fréquences calculées selon la loi de Hardy-Weinberg. Lorsque les systèmes comprennent de nombreux allèles, certains génotypes peuvent manquer ou n'être observés qu'en petit nombre. Le test de χ² est alors inapplicable, ou des regroupements de classes doivent être effectués, et une méthode dérivée de la méthode exacte de Fisher doit être appliquée.

Exemple de test $χ 2$ pour la déviation

Les données suivantes ont été fournies par E.B. Ford (1971) qui a noté les phénotypes observés dans une population de papillons écaille rouge. Une faible discordance génotype-phénotype peut être négligée. L'hypothèse nulle est que cette population répond à la loi de Hardy-Weingerg, l'hypothèse alternative étant qu'elle n'y répond pas.

Table 3: Loi de Hardy–Weinberg, exemple de calcul
Génotype	Tacheté blanc (AA)	Intermediaire (Aa)	Peu tacheté (aa)	Total
Nombre	1469	138	5	1612

D'où les fréquences alléliques peuvent être estimées :

$p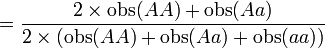$	$= {2 \times \mathrm{obs}(AA) + \mathrm{obs}(Aa) \over 2 \times (\mathrm{obs}(AA) + \mathrm{obs}(Aa) + \mathrm{obs}(aa))}$
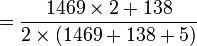
	$= {1469 \times 2 + 138 \over 2 \times (1469+138+5)}$
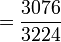
	$= { 3076 \over 3224}$
	$= 0.954$

$q$	$= 1 - p$
	$= 1 - 0.954$
	$= 0.046$

Les valeurs attendues sont :

$\mathrm{Exp}(AA) = p^2n = 0.954^2 \times 1612 = 1467.4$

$\mathrm{Exp}(Aa) = 2pqn = 2 \times 0.954 \times 0.046 \times 1612 = 141.2$

$\mathrm{Exp}(aa) = q^2n = 0.046^2 \times 1612 \leq 3.4$

Test du χ² :

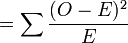
$χ 2$	$= \sum {(O - E)^2 \over E}$
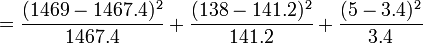
	$= {(1469 - 1467.4)^2 \over 1467.4} + {(138 - 141.2)^2 \over 141.2} + {(5 - 3.4)^2 \over 3.4}$
	$= 0.001 + 0.073 + 0.756$
	$= 0.83$

Il s'agit d'un test à un degré de liberté (ddl), -en règle, le nombre de degrés de liberté d'un test de χ² est de n − 1, où n est le nombre de classes, quoique qu'un autre ddl soit perdu, du fait que les valeurs attendues sont estimées à partir des valeurs observées. Le seuil de signification à 5% du χ², pour 1 ddl, est à 3.84. La valeur du χ² obtenue étant inférieure à 3.84, l'hypothèse nulle, à savoir la population étudiée suit la loi de Hardy-Weinberg, n'est pas rejetée.

Histoire

La génétique mendélienne a été redécouverte en 1900. Cependant, elle est restée plutôt sujet à controverses durant de nombreuses années et l'on ignorait alors de quelle manière elle pouvait déterminer des caractères continus. Udny Yule (1902) a critiqué le mendélisme car il pensait que les allèles dominants augmenteraient dans la population. L'américain William E. Castle (1903) a montré que sans sélection, les fréquences de génotypes resteraient stables. Karl Pearson (1903) découvrit une position d'équilibre avec des valeurs de p = q = 0,5. Reginald Punnett, incapable de rétorquer au point de vue de Yule, soumit le problème à G. H. Hardy, un mathématicien britannique, avec qui il jouait au cricket. Hardy était spécialisé en mathématiques pures et méprisait quelque peu les mathématiques appliquées ; son regard sur la façon dont les biologistes recouraient aux mathématiques est révélé dans un article de 1908 où il décrit cela comme « very simple ».

Citation (en anglais)

To the Editor of Science: I am reluctant to intrude in a discussion concerning matters of which I have no expert knowledge, and I should have expected the very simple point which I wish to make to have been familiar to biologists. However, some remarks of Mr. Udny Yule, to which Mr. R. C. Punnett has called my attention, suggest that it may still be worth making...

Suppose that Aa is a pair of Mendelian characters, A being dominant, and that in any given generation the number of pure dominants (AA), heterozygotes (Aa), and pure recessives (aa) are as p:2q:r. Finally, suppose that the numbers are fairly large, so that mating may be regarded as random, that the sexes are evenly distributed among the three varieties, and that all are equally fertile. A little mathematics of the multiplication-table type is enough to show that in the next generation the numbers will be as (p+q)^2:2(p+q)(q+r):(q+r)^2, or as p1:2q1:r1, say.

The interesting question is — in what circumstances will this distribution be the same as that in the generation before? It is easy to see that the condition for this is q^2 = pr. And since q_1^2 = p_1r_1, whatever the values of p, q, and r may be, the distribution will in any case continue unchanged after the second generation

Fin de citation

Le principe était donc connu comme Hardy's law (loi de Hardy) chez les anglophones jusqu'à ce que Curt Stern (1943) ne démontre qu'il avait déjà été formulé une première fois de façon indépendante en 1908 par le physicien allemand Wilhelm Weinberg (voir Crow 1999). D'autres ont essayé d'y associer le nom de Castle à cause de ses travaux en 1903, mais il est rare que l'on évoque la loi de Castle-Hardy-Weinberg.

Source

Cours de Génétique des populations (Mme Husté - Master Environnement - Rouen)
Les groupes sanguins chez l'homme, R.R. Race et R. Sanger, traduit par Ch. Salmon et A. Mourier, Masson et Cie éditeurs, 1970.
Immuno-hématologie et immunogénétique, M. Goudemand et Ch. Salmon, Flammarion Médecine-Sciences, 1980.
Bernstein F. (1930) Fortgesetzte Untersuchungen aus der Theorie der Blutgruppen. Z.indukt.abstamm. u. VerebLehre, 56, 233-237.
Dobson Aileen M., Ikin Elizabeth W. (1946). The ABO blood groups in the United Kingdom; frequencies based on a very large sample. J.Path.Bact., 48, 221-227
Roberts J.A.F. (1948) The frequencies of the ABO blood groups in South Western England. Ann. Eugen., Lond., 14, 109-116

Portail de l’origine et de l’évolution du vivant

Ce document provient de « Principe de Hardy-Weinberg ».

Catégories : Génétique des populations | Principe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Castle-Hardy-Weinberg de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires: