K-algèbre
- K-algèbre
-
Algèbre sur un corps
En mathématiques, une algèbre sur un corps commutatif est une structure algébrique qui se définit comme suit:
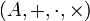 est une algèbre sur le corps
est une algèbre sur le corps  , ou simplement une
, ou simplement une  - algèbre si :
- algèbre si :
 est un corps commutatif,
est un corps commutatif,- (A, +, ·) est un espace vectoriel sur
 ,
,
- la loi × est définie de A x A dans A (loi de composition interne)
- la loi × est distributive, à gauche et à droite, par rapport à la loi + .
- pour tout (a, b) dans
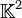 et pour tout (x, y) dans A2, (a·x)×(b·y) = (ab)·(x×y)
et pour tout (x, y) dans A2, (a·x)×(b·y) = (ab)·(x×y)
Définitions
Soient  un corps commutatif et A un espace vectoriel sur
un corps commutatif et A un espace vectoriel sur  contenant l'opération binaire (c'est-à-dire
contenant l'opération binaire (c'est-à-dire 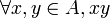 , est le « produit » de x et y). Si l'opération binaire est bilinéaire, ce qui signifie que
, est le « produit » de x et y). Si l'opération binaire est bilinéaire, ce qui signifie que 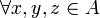 (vecteurs) et
(vecteurs) et 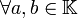 (scalaires), ces identités sont vraies :
(scalaires), ces identités sont vraies :
alors A est une algèbre sur  . On dit que A est une
. On dit que A est une  -algèbre où
-algèbre où  est la base de A. L'opérateur binaire est souvent désigné comme la multiplication dans A.
est la base de A. L'opérateur binaire est souvent désigné comme la multiplication dans A.
 peut être un anneau commutatif, dans ce cas, A et
peut être un anneau commutatif, dans ce cas, A et  forment un module. Dans ce cas, A est une
forment un module. Dans ce cas, A est une  -algèbre et
-algèbre et  est l'anneau de base de A.
est l'anneau de base de A.
Deux algèbres A et B sur  sont isomorphes s'il existe une bijection
sont isomorphes s'il existe une bijection 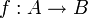 telle que f(xy) = f(x)f(y)
telle que f(xy) = f(x)f(y) 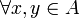 .
.
Propriétés
Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !
Exemples
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Structure externe
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article K-algèbre de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Algebre universelle — Algèbre universelle L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de… … Wikipédia en Français
Algèbre Universelle — L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de définir de manière… … Wikipédia en Français
ALGÈBRE — L’algèbre au sens moderne, à savoir l’étude des structures algébriques indépendamment de leurs réalisations concrètes, ne s’est dégagée que très progressivement au cours du XIXe siècle, en liaison avec le mouvement général d’axiomatisation de… … Encyclopédie Universelle
Algebre de Clifford — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algebre de Lie — Algèbre de Lie En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1 … Wikipédia en Français
Algebre semi-simple — Algèbre semi simple En mathématiques et plus particulièrement en algèbre, une A algèbre L, où A désigne un anneau, est qualifiée de semi simple ou de complètement réductible si et seulement si la structure d anneau associé à L l est Elle est… … Wikipédia en Français
Algèbre De Clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
Algèbre De Lie — En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1.1 Définition … Wikipédia en Français
Algèbre Semi-simple — En mathématiques et plus particulièrement en algèbre, une A algèbre L, où A désigne un anneau, est qualifiée de semi simple ou de complètement réductible si et seulement si la structure d anneau associé à L l est Elle est présente dans de… … Wikipédia en Français
Algèbre de Clifford du plan euclidien) — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algèbre de clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
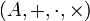 est une algèbre sur le corps
est une algèbre sur le corps  , ou simplement une
, ou simplement une  - algèbre si :
- algèbre si : est un corps commutatif,
est un corps commutatif, ,
,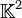 et pour tout (x, y) dans A2, (a·x)×(b·y) = (ab)·(x×y)
et pour tout (x, y) dans A2, (a·x)×(b·y) = (ab)·(x×y) un corps commutatif et A un espace vectoriel sur
un corps commutatif et A un espace vectoriel sur  contenant l'opération binaire (c'est-à-dire
contenant l'opération binaire (c'est-à-dire 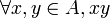 , est le « produit » de x et y). Si l'opération binaire est bilinéaire, ce qui signifie que
, est le « produit » de x et y). Si l'opération binaire est bilinéaire, ce qui signifie que 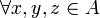 (vecteurs) et
(vecteurs) et 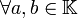 (scalaires), ces identités sont vraies :
(scalaires), ces identités sont vraies :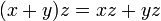 ;
;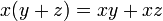 ;
;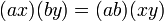 ,
, . On dit que A est une
. On dit que A est une  -algèbre où
-algèbre où  est la base de A. L'opérateur binaire est souvent désigné comme la multiplication dans A.
est la base de A. L'opérateur binaire est souvent désigné comme la multiplication dans A. peut être un anneau commutatif, dans ce cas, A et
peut être un anneau commutatif, dans ce cas, A et  forment un module. Dans ce cas, A est une
forment un module. Dans ce cas, A est une  -algèbre et
-algèbre et  est l'anneau de base de A.
est l'anneau de base de A. sont isomorphes s'il existe une bijection
sont isomorphes s'il existe une bijection 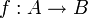 telle que f(xy) = f(x)f(y)
telle que f(xy) = f(x)f(y) 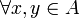 .
.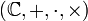 est une
est une  - algèbre associative et commutative.
- algèbre associative et commutative.
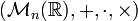 est une
est une  - algèbre associative et non commutative.
- algèbre associative et non commutative.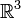 muni du produit vectoriel
muni du produit vectoriel 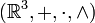 est une
est une  - algèbre non associative et non commutative.
- algèbre non associative et non commutative.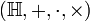 est une
est une  - algèbre associative et non commutative.
- algèbre associative et non commutative.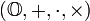 est une
est une  - algèbre non associative et non commutative.
- algèbre non associative et non commutative.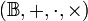 est une
est une  - algèbre associative et non commutative.
- algèbre associative et non commutative.
