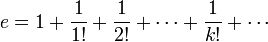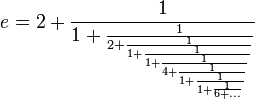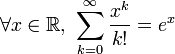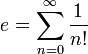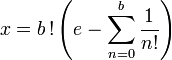Irrationalité de e

Irrationalité de e

e (nombre)

Article d'une série sur
la constante mathématique e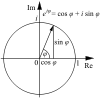
Euler's formula.svg
Logarithme naturel
Applications
Intérêts composés · Identité d'Euler et Formule d'Euler · Demi-vie et Croissance exponentielle/Décroissance exponentielle
Définitions
Démonstration de l'irrationalité de e · Représentations de e · Théorème de Lindemann-Weierstrass
Personnes
John Napier · Jacques Bernoulli · Leonhard Euler
Conjecture de Schanuel
Page d'aide sur l'homonymie Pour les articles homonymes, voir E.

e est une constante mathématique dont l'expression décimale commence par 2,718 281 828 459 045 235 360 287 4…. Il s'agit de la base des logarithmes naturels.

Appellation :

  • e est parfois appelée constante de Néper, du nom du mathématicien écossais John Napier qui introduisit les logarithmes.
  • e fut appelé nombre exponentiel par Euler en 1761.

Sommaire

Considérations historiques

Le nombre e est probablement la constante réelle la plus importante des mathématiques après π : on la retrouve en effet dans la normalisation des fonctions exponentielles. Il est cependant difficile de dater avec exactitude son apparition dans la littérature. En effet, si Neper introduit les logarithmes comme artifice de calcul pour simplifier les calculs du sinus, du cosinus, du produit et du quotient, il ne précise pas de base particulière pour ces logarithmes et les logarithmes les plus courants à cette époque sont ceux en base 10.

Les logarithmes naturels apparaissent pour la première fois en 1618 en appendice d'un traité de Napier probablement rédigé par William Oughtred.

En 1624, Briggs donne l'approximation du logarithme décimal d'un nombre qu'il n'identifie pas avec précision, mais qui se révèle être e.

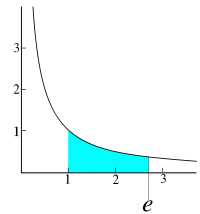
L'aire sous l'hyperbole est égale à 1 sur l'intervalle [1;e].

En 1647, Grégoire de Saint-Vincent calcule l'aire sous l'hyperbole, mais ne met pas en évidence le nombre e.

En 1661, Huygens est capable de faire le rapprochement entre l'aire sous l'hyperbole et les fonctions logarithmes. Comme e est le réel tel que l'aire sous l'hyperbole entre 1 et e vaille 1, il est probable que ce nombre fut remarqué à cette époque sans toutefois que l'on parle pour lui de la base du logarithme naturel.

La première apparition de e comme nombre remarquable date de 1683, époque à laquelle Bernoulli s'intéresse aux calculs d'intérêt. Ce qui l'amène à étudier la limite de la suite 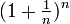(1 + \tfrac 1n)^n. Mais personne à ce moment ne fait le rapprochement entre ce nombre et les logarithmes naturels. Pourtant c'est durant cette période que l'on commence à entrevoir que la fonction logarithme de base a est la réciproque de la fonction exponentielle de base a. La communauté scientifique est alors mûre pour découvrir e. C'est dans une lettre de Leibniz à Huygens que ce nombre est enfin identifié comme la base du logarithme naturel, mais Leibniz lui donne le nom de b.

On doit la notation e pour cette constante à Euler dans une lettre que celui-ci adresse à Goldbach en 1731. Le choix de e a donné lieu a de nombreuses conjectures : e pour Euler ? e pour exponentielle ? ou tout simplement e comme première voyelle disponible dans le travail d'Euler.

C'est aussi Euler qui donne le développement de e en série

e = 1 + \dfrac{1}{1!} + \dfrac{1}{2!} + \cdots + \dfrac{1}{k!}+ \cdots

et en fraction continue :

e=2+\frac{1}{1+\frac{1}{2+\frac{1}{1+\frac{1}{1+\frac{1}{4+\frac{1}{1+\frac{1}{1+\frac{1}{6+\ldots}}}}}}}}

Puisque e possède un développement en fraction continue infini, il est irrationnel. Les différents approximants de Padé permettent d'offrir de nombreuses expressions de e sous forme de fractions continues généralisées (cf. l'article Approximant de Padé de la fonction exponentielle). Elles permettent à Charles Hermite de démontrer la transcendance de ce nombre en 1873.

Décimales connues

Le nombre de décimales connues de la constante e a augmenté de façon spectaculaire au cours des dernières décennies. Cette précision est due à l'augmentation des performances des ordinateurs ainsi qu'au perfectionnement des algorithmes[1],[2].

Nombre de décimales connues de la constante e
Date Décimales connues Performance due à
1748 18 Leonhard Euler[3]
1853 137 William Shanks
1871 205 William Shanks
1884 346 J. Marcus Boorman
1946 808  ?
1949 2 010 John von Neumann (avec l'ENIAC)
1961 100 265 Daniel Shanks & John W. Wrench
1981 116 000 Stephen Gary Wozniak (avec l'Apple II[4])
1994 10 000 000 Robert Nemiroff & Jerry Bonnell
Mai 1997 18 199 978 Patrick Demichel
Août 1997 20 000 000 Birger Seifert
Septembre 1997 50 000 817 Patrick Demichel
Février 1999 200 000 579 Sebastian Wedeniwski
Octobre 1999 869 894 101 Sebastian Wedeniwski
21 novembre 1999 1 250 000 000 Xavier Gourdon
10 juillet 2000 2 147 483 648 Shigeru Kondo & Xavier Gourdon
16 juillet 2000 3 221 225 472 Colin Martin & Xavier Gourdon
2 août 2000 6 442 450 944 Shigeru Kondo & Xavier Gourdon
16 août 2000 12 884 901 000 Shigeru Kondo & Xavier Gourdon
21 août 2003 25 100 000 000 Shigeru Kondo & Xavier Gourdon
18 septembre 2003 50 100 000 000 Shigeru Kondo & Xavier Gourdon
27 avril 2007 100 000 000 000 Shigeru Kondo & Steve Pagliarulo

Définitions et propriétés

Définitions de e

Les considérations précédentes montrent que e peut être défini de plusieurs façons différentes

  • e est le réel tel que ln(e) = 1 lorsqu'on définit la fonction ln comme la primitive de la fonction x \to \tfrac{1}{x} qui s'annule en 1. C'est la raison pour laquelle cette constante est aussi appelée la base des logarithmes naturels
  • e est le réel tel que exp(1) = e lorsqu'on définit la fonction exp comme l'unique fonction vérifiant u' = u et u(0) = 1.
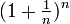  • e est la limite de la suite (1 + \tfrac 1n)^n.
  • e est égal à la somme de la série infinie 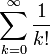\displaystyle\sum_{k=0}^\infty \dfrac{1}{k!} (avec la convention 0! = 1).

L'équivalence de ces quatre définitions provient des relations qui lient la fonction exponentielle, la fonction logarithme et les limites de suites.

Théorie des nombres

Leonhard Euler

La constante de Néper apparaît largement dans la théorie des nombres. Les mathématiciens se sont très tôt intéressés à la nature du nombre e. L'irrationalité de e fut démontrée par Lambert en 1761 et plus tard par Euler. La démonstration peut se faire grâce à son développement en série (voir la démonstration de l'irrationalité de e, ci-dessous) soit par son développement en fraction continue.

La preuve de la transcendance de e fut établie par Hermite en 1873. On en déduit que, pour tout rationnel r non nul (ce qui inclut les entiers naturels), er est aussi transcendant, mais on ne sait pas encore (2007) si ee est transcendant ou non.

Les propriétés de ce nombre sont à la base du théorème de Lindemann-Weierstrass.

Il a été conjecturé que e était un nombre normal.

Fonction exponentielle et équation différentielle

Pour tout réel x, exp(x) = ex où exp est l'unique fonction y vérifiant l'équation différentielle y' = y et y(0) = 1. Cette fonction est appelée fonction exponentielle de base e.

Elle permet de donner toutes les solutions de l'équation différentielle y' = ay qui sont les fonctions définies par f(x) = Ceax.

La fonction exponentielle admet le développement en série suivant :

\forall x \in \R,\ \sum_{k=0}^\infty \frac{x^k}{k!} = e^x

Fonction trigonométrique

La recherche de l'unique solution complexe à l'équation différentielle u' = iu et u(0) = 1 conduit à la fonction u(x) = eix = cos(x) + isin(x) et à l'identité d'Euler :

eiπ + 1 = 0

qui selon Richard Feynman est « la formule la plus remarquable du monde »[5] (e représentant l'analyse, i l'algèbre, π la géométrie, 1 l'arithmétique et le nombre 0 les mathématiques). Euler lui-même aurait également été émerveillé de cette relation rassemblant cinq nombres fondamentaux : 0, 1, e, i, π.

Démonstration de l'irrationalité de e

Le nombre e est égal à la somme de la série de l'exponentielle de 1 :

e = \sum_{n = 0}^{\infty} \dfrac{1}{n!}

Ce développement peut être employé pour montrer qu'il est irrationnel.

Démonstration, par l'absurde. Supposons qu'il existe deux entiers a et b tels que 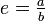e=\tfrac{a}{b}, où a est strictement positif et b strictement supérieur à 1. Considérons le nombre

x = b\,!\left(e - \sum_{n = 0}^{b} \dfrac{1}{n!}\right)

Nous allons démontrer que x est un nombre entier strictement positif et strictement inférieur à 1, et cette contradiction établira l'irrationalité de e.

  • Pour voir que x est un nombre entier, remarquons que
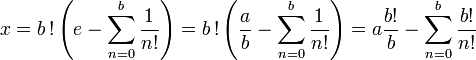
x = b\,!\left(e - \sum_{n = 0}^{b} \dfrac{1}{n!}\right) = b\,!\left(\dfrac{a}{b} - \sum_{n = 0}^{b} \dfrac{1}{n!}\right)= a \dfrac{b!}{b} - \sum_{n = 0}^{b} \dfrac{b!}{n!}
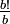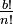Or, b divise b! et, pour tout entier n compris entre 0 et b, n! divise b!, les quantités \tfrac{b!}{b} et \tfrac{b!}{n!} sont donc entières, x est donc entier comme somme et différence d'entiers.
  • Pour voir que x est un nombre strictement positif et strictement inférieur à 1, remarquons que
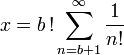x = b\,!\sum_{n = b+1}^{\infty} \dfrac{1}{n!} et ainsi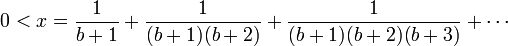
0 < x = \dfrac{1}{b+1} + \dfrac{1}{(b+1)(b+2)} + \dfrac{1}{(b+1)(b+2)(b+3)} + \cdots
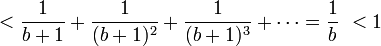
< \dfrac{1}{b+1} + \dfrac{1}{(b+1)^2} + \dfrac{1}{(b+1)^3} + \cdots = \dfrac{1}{b} \ < 1
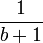Ici, la dernière somme est une série géométrique de raison \dfrac{1}{b+1}.

Puisqu'il n'existe aucun nombre entier strictement positif et strictement inférieur à 1, nous avons obtenu une contradiction, et ainsi e doit être irrationnel. ∎CQFD

Une autre démonstration consiste à établir le développement en fraction continue du nombre e. Si la preuve est plus complexe, elle offre aussi plus de possibilités de généralisation. Elle permet de montrer que si x est un nombre rationnel non nul, alors ex est irrationnel. Elle permet aussi d'établir que e n'est pas un irrationnel quadratique, c'est-à-dire n'est solution d'aucune équation du second degré à coefficients rationnels (cf. Fraction continue et approximation diophantienne). En revanche, pour aller plus loin, c'est-à-dire que pour montrer que e n'est solution d'aucune équation du troisième degré à coefficients rationnels, puis qu'il est transcendant, ce qui signifie qu'il n'est solution d'aucune équation polynomiale à coefficients rationnels, de nouvelles idées sont nécessaires.

Notes et références

  1. ↑ Sebah, P. and Gourdon, X.; (en)The constant e and its computation
  2. ↑ Gourdon, X.; (en)Reported large computations with PiFast
  3. ↑ (en)New Scientist 21st July 2007 p. 40
  4. ↑ (en)Byte Magazine vol.  6, Issue 6 (June 1981) p. 392) "The Impossible Dream: Computing e to 116,000 places with a Personal Computer"
  5. ↑ Equations as icons

Voir aussi

Articles connexes

Notion de nombre
Ensembles usuels \mathbb{N} Entier naturel • \mathbb{Z} Entier relatif • \mathbb{D} Nombre décimal • \mathbb{Q} Nombre rationnel • \mathbb{R} Nombre réel • \mathbb{C} Nombre complexe Mathématiques
Extensions \mathbb{H} Quaternion • \mathbb{O} Octonion • \mathbb{S} Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • \mathbb{Q}_p Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

Liens externes

  • Portail des mathématiques Portail des mathématiques

Ce document provient de « E (nombre) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Irrationalité de e de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • irrationalité — [ irasjɔnalite ] n. f. • 1845; de irrationnel ♦ Caractère de ce qui est irrationnel; l irrationnel. Irrationalité d un principe. ● irrationalité nom féminin Caractère, état de ce qui est irrationnel. ● irrationalité (synonymes) nom féminin… …   Encyclopédie Universelle

  • Irrationalité — Rationalité En sciences humaines et sociales (psychologie, psychologie sociale), et en économie, la rationalité caractérise une conduite cohérente, voire optimale, par rapport aux buts de l individu. Se pose toutefois la question de la… …   Wikipédia en Français

  • Démonstration de l'irrationalité de e — e (nombre) Article d une série sur la constante mathématique e …   Wikipédia en Français

  • Racine carrée de deux — La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu’il est multiplié par lui même, donne le nombre 2, autrement dit √2 × √2 = 2. C’est un nombre irrationnel, dont une valeur approchée à 10 9… …   Wikipédia en Français

  • Constante de Pythagore — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine Carrée De 2 — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine Carrée De Deux — L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine De 2 — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine De Deux — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine carree de deux — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”