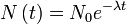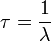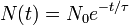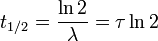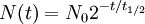- Decroissance exponentielle
-
Décroissance exponentielle
 La décharge d'un condensateur est une décroissance exponentielle.
La décharge d'un condensateur est une décroissance exponentielle.
Article d'une série sur la constante mathématique e 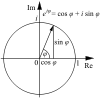
Logarithme naturel Applications Intérêts composés · Identité d'Euler et Formule d'Euler · Demi-vie et Croissance exponentielle/Décroissance exponentielle Définitions Démonstration de l'irrationalité de e · Représentations de e · Théorème de Lindemann-Weierstrass Personnes John Napier · Jacques Bernoulli · Leonhard Euler Conjecture de Schanuel Une quantité est dite sujette à une décroissance exponentielle si elle diminue à un taux proportionnel à sa valeur. Mathématiquement, cela peut être exprimé par l'équation différentielle suivante, avec N la quantité et λ un nombre positif appelé la « constante de décroissance » :
La solution de cette équation est, en notant N0 la valeur de N à l'instant t = 0 :
Sommaire
Démonstration
Remarque : si λ est négatif, on a plutôt croissance exponentielle du phénomène.
On part de la définition sous forme d'une équation différentielle :
En séparant les variables, on obtient :
Alors, en intégrant entre l'instant initial et t :
Ce qui s'intègre en :
Soit enfin :
Quantités dérivées
Durée de vie moyenne
Si on considère que la quantité N qui décroît est discrète, c'est-à-dire que N mesure le nombre d'élément d'un ensemble, alors on peut donner une expression de la durée de vie moyenne d'un élément dans cet ensemble :
On l'appelle aussi « constante de temps ». N vérifie alors :
Demi-vie
Il est plus courant de faire usage de la demi-vie d'un système à décroissance radioactive, qui correspond à la durée au bout de laquelle la quantité N est divisée par 2. On note souvent cette durée t1 / 2. Elle est reliée à la constante de décroissance et à la constante de temps par les relations :
On peut également remplacer l'exponentielle de l'expression de la demi-vie pour obtenir :
Utilisation
En physique, la décroissance exponentielle est caractéristique des phénomènes sans vieillissement, c'est-à-dire qui se produisent avec une égale probabilité quelle qu'ait été leur durée de vie, par exemple dans le suivi de la désintégration radioactive.
En biologie, une telle décroissance peut modéliser l'élimination d'un produit dans le sang, au cours du temps.
Voir aussi
Articles connexes
- Portail des mathématiques
- Portail de la physique
Catégories : Équation différentielle | Exponentielle
Wikimedia Foundation. 2010.

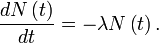
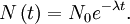
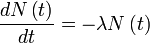
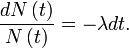
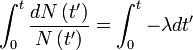
![ln \left[ N \left( t \right) \right] - ln \left[ N_0 \right] = - \lambda t](/pictures/frwiki/102/f0c607a0d00bb2693fa2a7131ee5ca86.png)