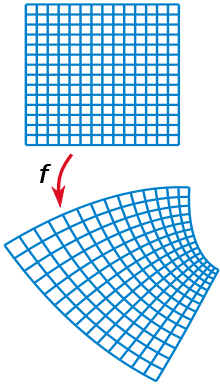
- Fonction holomorphe
-
En analyse complexe, une fonction holomorphe est une fonction à valeurs dans
 , définie et dérivable en tout point d'un sous-ensemble ouvert du plan complexe
, définie et dérivable en tout point d'un sous-ensemble ouvert du plan complexe  .
.Cette condition est beaucoup plus forte que la dérivabilité réelle. Elle entraîne (via la théorie de Cauchy) que la fonction est analytique : elle est indéfiniment dérivable et est égale au voisinage de tout point de l'ouvert à la somme de sa série de Taylor. Un fait remarquable en découle : les notions de fonction analytique complexe et de fonction holomorphe coïncident. Pour cette raison, les fonctions holomorphes constituent le pilier central de l'analyse complexe.
Définition
Définition — Soient U un sous-ensemble ouvert (non vide) de l'ensemble
 des nombres complexes et une fonction
des nombres complexes et une fonction  .
.- On dit que f est dérivable (au sens complexe) ou holomorphe en un point z0 de U si la limite suivante, appelée dérivée de f en z0 existe :
- On dit que f est holomorphe sur l'ouvert U si elle est holomorphe en tout point z0 de U. En particulier, on appelle fonction entière une fonction holomorphe dans tout le plan complexe.
La limite est prise ici sur toutes les suites de nombres complexes tendant vers z0, et pour toutes ces suites le quotient doit tendre vers un même nombre f '(z0). Intuitivement, si f est dérivable au sens complexe en z0, et si l'on approche le point z0 dans la direction d'un vecteur u, alors (pourvu que f '(z0) ≠ 0) les images approchent le point f(z0) dans la direction du vecteur f '(z0) u (produit des nombres complexes f '(z0) et u).
Exemples
- Toute fonction polynomiale à coefficients complexes est holomorphe sur
 .
. - Toute fonction rationnelle à coefficients complexes est holomorphe sur le complémentaire de l'ensemble de ses pôles. Par exemple, la fonction inverse
 est holomorphe sur
est holomorphe sur  .
. - Soit
 une série entière à coefficients complexes de rayon de convergence non nul (fini ou non) ; on note D son disque de convergence.
une série entière à coefficients complexes de rayon de convergence non nul (fini ou non) ; on note D son disque de convergence.
- La fonction
 définie par
définie par  est holomorphe, et pour tout
est holomorphe, et pour tout  ,
,  .
. - En fait, cette fonction est indéfiniment dérivable sur D.
- La fonction exponentielle est holomorphe sur
 . Il en est de même des fonctions trigonométriques (qui peuvent être définies à partir de la fonction exponentielle au moyen des formules d'Euler) et des fonctions hyperboliques.
. Il en est de même des fonctions trigonométriques (qui peuvent être définies à partir de la fonction exponentielle au moyen des formules d'Euler) et des fonctions hyperboliques. - On appelle détermination du logarithme sur un ouvert
 de
de  toute fonction holomorphe
toute fonction holomorphe  telle que
telle que  . On a alors :
. On a alors :  .
.
- Sur tout ouvert U de
 où existe une détermination L du logarithme, on peut définir, quel que soit
où existe une détermination L du logarithme, on peut définir, quel que soit  , la fonction
, la fonction  . Chacune de ces fonctions est une détermination du logarithme sur U, et réciproquement, si U est connexe, toute détermination du logarithme sur U est l'une de ces fonctions.
. Chacune de ces fonctions est une détermination du logarithme sur U, et réciproquement, si U est connexe, toute détermination du logarithme sur U est l'une de ces fonctions. - L'existence sur un ouvert connexe U de
 d'une détermination du logarithme équivaut à l'existence d'une fonction
d'une détermination du logarithme équivaut à l'existence d'une fonction  holomorphe sur cet ouvert, telle que
holomorphe sur cet ouvert, telle que  pour tout
pour tout  ; dans ce cas, il existe (au moins) une constante complexe C telle que la fonction
; dans ce cas, il existe (au moins) une constante complexe C telle que la fonction  soit une détermination du logarithme sur U.
soit une détermination du logarithme sur U.
- Il n'existe pas de détermination du logarithme sur l'ouvert
 .
. - Il existe une détermination du logarithme sur l'ensemble des nombres complexes privé de la demi-droite des réels négatifs ou nuls (on parle de "coupure"). Parmi toutes les déterminations du logarithme sur cet ouvert, il en existe une et une seule qui prolonge le logarithme népérien réel.
- Plus généralement, il existe une détermination du logarithme sur tout ouvert simplement connexe ne contenant pas 0.
- Il n'existe pas de détermination du logarithme sur l'ouvert
- Sur tout ouvert U de
- Sur tout ouvert U de
 où existe une détermination L du logarithme, on peut définir une détermination de la puissance d'exposant
où existe une détermination L du logarithme, on peut définir une détermination de la puissance d'exposant  (où
(où  ), en posant
), en posant
 .
.- En particulier, si n est un entier naturel supérieur ou égal à 2, la fonction

- est holomorphe sur U et vérifie l'identité
 .
. - On dit que cette fonction est une détermination sur U de la racine n-ième.
- On peut noter
![\ \sqrt[n]{z}](1/ec103ebd5128c3ec96e1f29b8ecad889.png) au lieu de
au lieu de  (si des réels strictement positifs appartiennent à U, il se peut qu'il y ait alors conflit entre cette notation, et sa signification habituelle, servant à désigner la racine n-ième positive).
(si des réels strictement positifs appartiennent à U, il se peut qu'il y ait alors conflit entre cette notation, et sa signification habituelle, servant à désigner la racine n-ième positive).
- Les fonctions trigonométriques réciproques ont de la même manière des coupures et sont holomorphes partout sauf aux coupures.
Propriétés
Généralités
Parce que la dérivation complexe est linéaire et qu'elle obéit aux règles classiques de dérivation, les sommes, produits ou composées de fonctions holomorphes sont holomorphes, et le quotient de deux fonctions holomorphes est holomorphe sur tout ouvert où le dénominateur ne s'annule pas.
Les règles de calcul des dérivées au sens complexe sont identiques à celles des dérivées des fonctions d'une variable réelle : linéarité, dérivée d'un produit, d'un quotient, d'une fonction composée.
Une fonction holomorphe en un point est bien évidemment continue en ce point.
Près d'un point z0 où la dérivée d'une fonction holomorphe f est non nulle, f est une transformation conforme, c'est-à-dire qu'elle préserve les angles (orientés) et les formes de petites figures (mais pas les longueurs, en général).
En effet, sa différentielle au point z0 est l'application
 -linéaire
-linéaire  , où A = f'(z0) : la différentielle s'identifie donc à une similitude directe du plan, sous réserve que A soit non nul.
, où A = f'(z0) : la différentielle s'identifie donc à une similitude directe du plan, sous réserve que A soit non nul.Équations de Cauchy-Riemann
Article détaillé : équations de Cauchy-Riemann.Si l'on identifie
 à
à  , alors les fonctions holomorphes sur un ouvert de
, alors les fonctions holomorphes sur un ouvert de  coïncident avec les fonctions de deux variables réelles qui sont
coïncident avec les fonctions de deux variables réelles qui sont  -différentiables sur cet ouvert et y vérifient les équations de Cauchy-Riemann, un système de deux équations aux dérivées partielles :
-différentiables sur cet ouvert et y vérifient les équations de Cauchy-Riemann, un système de deux équations aux dérivées partielles :On considère une fonction
 d'une variable complexe, où U est un ouvert du plan complexe
d'une variable complexe, où U est un ouvert du plan complexe  . On utilise ici les notations suivantes :
. On utilise ici les notations suivantes :- la variable complexe
 est notée
est notée  , où x, y sont réels
, où x, y sont réels - les parties réelle et imaginaire de
 sont notées respectivement
sont notées respectivement  et
et  , c'est-à-dire :
, c'est-à-dire :  , où
, où  sont deux fonctions réelles de deux variables réelles.
sont deux fonctions réelles de deux variables réelles.
Équations de Cauchy-Riemann — Les quatre propositions suivantes sont équivalentes :
- f est holomorphe en un point zo de U

 et
et 
 , où l'opérateur différentiel
, où l'opérateur différentiel  est, par définition, égal à
est, par définition, égal à  .
.
Remarque, toujours avec f holomorphe en zo :
 où l'opérateur différentiel
où l'opérateur différentiel  est, par définition, égal à
est, par définition, égal à  .
.Conséquences des équations de Cauchy Riemann : avec les notations ci dessus, les laplaciens de la partie réelle et de la partie imaginaire de f sont nuls :
P et Q sont dits harmoniques conjuguées, ce sont des fonctions harmoniques.
(plus loin le caractère
 des fonctions holomorphes est montré (voir formule intégrale de Cauchy), d'où l'existence des laplaciens.)
des fonctions holomorphes est montré (voir formule intégrale de Cauchy), d'où l'existence des laplaciens.)On a également :

Inversement, soit P une fonction harmonique. Alors on peut construire une fonction holomorphe f telle que P soit la partie réelle de f (ou indifféremment sa partie imaginaire), il suffit pour cela de construire la partie imaginaire Q (ou réelle si on veut P comme partie imaginaire) grâce aux équations de Cauchy-Riemann, par équivalence avec l'holomorphie.
Intégrale curviligne le long de différents chemins strictement homotopes
Quel que soit un chemin homotope continu et continument dérivable par morceaux dans un ouvert reliant deux points de cet ouvert, la valeur de l'intégrale curviligne sur ce chemin d'une fonction qui est holomorphe sur ce même ouvert, est toujours la même, elle ne dépend pas du chemin entre ces deux points. Autrement dit :
Propriété — Soit f une fonction holomorphe sur un ouvert U du plan complexe
 .
.Quels que soient γ et Γ deux chemins de U strictement homotopes dans U, et qui sont de plus continument dérivable par morceaux, on a :
Rappel : deux chemins sont dits strictement homotopes dans U s'ils sont homotopes dans U et de mêmes extrémités.
Cette propriété peut se démontrer de deux manières :
- soit grâce à une conséquence de l'holomorphie de
 : le théorème intégral de Cauchy (voir plus loin) dont il est une énonciation un peu différente, en prenant deux chemins strictement homotopes. En effet leur réunion est un chemin fermé, contenu dans un ouvert connexe simple sur lequel
: le théorème intégral de Cauchy (voir plus loin) dont il est une énonciation un peu différente, en prenant deux chemins strictement homotopes. En effet leur réunion est un chemin fermé, contenu dans un ouvert connexe simple sur lequel  est holomorphe et le résultat est alors évident par application. Toutefois il faut préalablement démontrer le théorème de Cauchy, ce qui peut se faire grâce à la formule de Green Riemann.
est holomorphe et le résultat est alors évident par application. Toutefois il faut préalablement démontrer le théorème de Cauchy, ce qui peut se faire grâce à la formule de Green Riemann. - soit directement à partir du caractère holomorphe de
 (c'est la démonstration qui suit), et alors on peut parvenir à démontrer le théorème de Cauchy d'une autre manière.
(c'est la démonstration qui suit), et alors on peut parvenir à démontrer le théorème de Cauchy d'une autre manière.
DémonstrationSoit
![\Gamma : \mathbb[a;b] \to U](3/f7360df77fda5487d22efaffbd596aa9.png) , continu et continument dérivable. C'est donc un chemin de U. Soit
, continu et continument dérivable. C'est donc un chemin de U. Soit ![\gamma : \mathbb[c;d] \to U](9/329d5ffa67c31f9cdd49c847d8d5e93f.png) , un chemin strictement homotope à Γ dans U. Grâce à un changement de variable C1 difféomorphisme adapté à chaque intervalle de départ, on peut ramener ces deux intervalles à [0;1] (un changement de variable affine convient). Par exemple, pour Γ, soit le changement de variable adapté Φ :
, un chemin strictement homotope à Γ dans U. Grâce à un changement de variable C1 difféomorphisme adapté à chaque intervalle de départ, on peut ramener ces deux intervalles à [0;1] (un changement de variable affine convient). Par exemple, pour Γ, soit le changement de variable adapté Φ :![\int_\Gamma f(z) \,dz = \int_{[a;b]} f(\Gamma(t)) \Gamma'(t) \,dt = \int_{[0;1]} f(\Gamma(\Phi^{-1}(u))) \Gamma'(\Phi(u)) \Phi'(u) \,du](f/5ef1473019a3a75a05947a15496a5222.png)
Le paramétrage du chemin change (de
 à
à  ) mais pas la valeur de l'intégrale. Donc pour simplifier, dans la suite a et c vaudront zéro et b et d vaudront 1.
) mais pas la valeur de l'intégrale. Donc pour simplifier, dans la suite a et c vaudront zéro et b et d vaudront 1.
Par définition de l'homotopie stricte, il existe une application![H: \mathbb[0,1]*[0,1] \to U](d/15d088cbaee9a691b406d1593b14fa1e.png) continue. Avec, pour tout t dans [0,1], H(0,t) = Γ(t) et H(1,t) = γ(t), et pour tout s dans [0;1]:H(s,0) = H(0,0) et H(s,1) = H(0,1) (extrémités fixes).
continue. Avec, pour tout t dans [0,1], H(0,t) = Γ(t) et H(1,t) = γ(t), et pour tout s dans [0;1]:H(s,0) = H(0,0) et H(s,1) = H(0,1) (extrémités fixes).
Le but de la démonstration est donc de montrer que l'intégrale , fonction de s est constante, ce qui implique en particulier l'égalité entre l'intégrale le long de γ (en s=1) et celle le long de Γ (en s=0), prouvant ainsi le résultat.
, fonction de s est constante, ce qui implique en particulier l'égalité entre l'intégrale le long de γ (en s=1) et celle le long de Γ (en s=0), prouvant ainsi le résultat.A priori H n'est pas C2 mais ceci sera supposé dans un premier temps. Puis le cas général H continue sera ramené grâce à la densité de l'espace des fonctions continues sur [0;1]x[0;1] dans l'espace des fonctions C2.

L'égalité qui suit fait appel au théorème de Leibniz, en effet les conditions sont vérifiées :
 est intégrable sur [0;1]
est intégrable sur [0;1] est C1 sur [0;1]
est C1 sur [0;1]- La dérivée partielle par rapport à s de l'intégrande est borné car les fonctions constituant l'intégrande sont continues et continument dérivables, donc quel que soit s dans [0;1] une fonction constante convenable domine la dérivée partielle par rapport à s intégrande, et l'intervalle d'intégration étant borné cette constante est elle-même intégrable.
![g'(s)=\int_0^1 \frac{\partial [f(H(s,t))\frac{\partial H(s,t)}{\partial t}]}{\partial s}\, dt](8/248be3470cb93475e649805cd89cb8de.png)
L'égalité qui suit fait, quant à elle, appel au caractère holomorphe de f :
![g'(s)=\int_0^1 [\frac{\partial H(s,t)}{\partial t} \frac{\partial H(s,t)}{\partial s}f'(H(s,t))+f(H(s,t))\frac{\partial^2 H(s,t)}{\partial s \partial t}]dt](7/cc779f59af0c65622c2837dacba9cdb3.png)
Le premier terme de l'intégrande est la dérivée par rapport à t de f(H(s,.)), multiplié par la dérivée partielle par rapport à s de H. Donc en l'intégrant par parties, puis en simplifiant (grâce au théorème de Schwarz, qui s'applique car H est C2) avec le second terme de l'intégrande ci-dessus :

Comme les extrémités sont fixes :
 , donc on a g'(s) = 0.
, donc on a g'(s) = 0.
Retour au cas H continue : la densité de l'ensemble des fonctions continues dans l'ensemble des fonctions C2 permet d'affirmer qu'il existe une suite (Hn) de fonctions de C2, convergeant uniformément vers H. À chaque fonction Hn on associe la fonction . Pour ces fonctions, le résultat ci dessus s'applique, et donc pour tout n, gn(0) = gn(1).
. Pour ces fonctions, le résultat ci dessus s'applique, et donc pour tout n, gn(0) = gn(1).Pour pouvoir passer à la limite et ainsi conclure, il faut maintenant prouver que gn converge uniformément vers g.

Où
 est la norme infinie définie dans l'espace des fonctions continues sur [0;1], auxquelles appartiennent les gn ainsi que g.
est la norme infinie définie dans l'espace des fonctions continues sur [0;1], auxquelles appartiennent les gn ainsi que g.Comme
 converge uniformément vers
converge uniformément vers  et
et  converge uniformément vers
converge uniformément vers  , l'intégrande à droite tend vers zéro, donc gn converge uniformément sur [0;1] vers g, en particulier comme gn(0) = gn(1) alors par passage à la limite g(0) = g(1), ce qui prouve le résultat.
, l'intégrande à droite tend vers zéro, donc gn converge uniformément sur [0;1] vers g, en particulier comme gn(0) = gn(1) alors par passage à la limite g(0) = g(1), ce qui prouve le résultat.Lemme de Goursat
Article détaillé : Lemme de Goursat (analyse complexe).Énoncé du lemme de Goursat pour les rectangles — Si f est une fonction d'une variable complexe définie et dérivable (holomorphe) sur un voisinage ouvert d'un rectangle R, alors l'intégrale curviligne de f sur le contour
 de R est nulle :
de R est nulle :-
 .
.
Ce résultat reste vrai si
 n'est pas holomorphe sur un nombre fini de points de l'ouvert considéré, tout en y restant continue.
n'est pas holomorphe sur un nombre fini de points de l'ouvert considéré, tout en y restant continue.Énoncé du lemme de Goursat pour les triangles — Si
 est une fonction d'une variable complexe définie et dérivable (holomorphe) sur un voisinage ouvert d'un triangle
est une fonction d'une variable complexe définie et dérivable (holomorphe) sur un voisinage ouvert d'un triangle  , alors l'intégrale curviligne de
, alors l'intégrale curviligne de  sur le contour
sur le contour  de
de  est nulle :
est nulle :-
 .
.
Ce résultat reste vrai si
 n'est pas holomorphe sur un nombre fini de points de l'ouvert considéré, tout en y restant continue.
n'est pas holomorphe sur un nombre fini de points de l'ouvert considéré, tout en y restant continue.Ces lemmes peuvent se démontrer de deux manières :
- soit comme une application du théorème intégral de Cauchy (voir plus loin), qu'il faut préalablement démontrer grâce par exemple à la formule de Green Riemann. Attention, comme application du théorème de Cauchy on ne montre pas le résultat dans le cas où
 n'est pas holomorphe sur un nombre fini de points où elle est néanmoins continue.
n'est pas holomorphe sur un nombre fini de points où elle est néanmoins continue. - soit (c'est la démonstration proposée dans l'article détaillé) directement à partir du caractère holomorphe de f et on peut alors montrer le théorème de Cauchy d'une autre manière.
Primitive d'une fonction holomorphe
propriété — Soit
 une fonction holomorphe sur un ouvert
une fonction holomorphe sur un ouvert  connexe simple. Soit la fonction
connexe simple. Soit la fonction  , où
, où  est un point de
est un point de  et
et  est un chemin de
est un chemin de  entre
entre  et
et  .
.Alors
 est une primitive de
est une primitive de  sur
sur  .
.Il est important que le connexe soit simple, ainsi l'intégrale entre deux points de
 ne dépend pas du chemin entre ces deux points.
ne dépend pas du chemin entre ces deux points.Par exemple, la fonction
 est holomorphe sur
est holomorphe sur  qui est connexe mais pas simple. L'intégrale de
qui est connexe mais pas simple. L'intégrale de  sur le cercle de centre 0 de rayon 1 (parcouru dans le sens trigonométrique), vaut 2πi, mais vaut 0 sur un chemin fermé joignant 1 à lui même en n'entourant pas 0. On peut en revanche définir une primitive de
sur le cercle de centre 0 de rayon 1 (parcouru dans le sens trigonométrique), vaut 2πi, mais vaut 0 sur un chemin fermé joignant 1 à lui même en n'entourant pas 0. On peut en revanche définir une primitive de  sur n'importe quelle ensemble du type
sur n'importe quelle ensemble du type  où
où  est une demi droite de
est une demi droite de  d'extrémité 0, un tel ensemble est en effet connexe, et une primitive est une détermination du logarithme sur cet ensemble, à une constante près.Démonstration
d'extrémité 0, un tel ensemble est en effet connexe, et une primitive est une détermination du logarithme sur cet ensemble, à une constante près.DémonstrationLa démonstration proposée ici se déroule en deux temps : tout d'abord l'existence de primitives dans le cas d'une fonction holomorphe sur un ouvert convexe est prouvée, puis ce résultat est utilisé pour généraliser au cas d'une fonction holomorphe sur un ouvert connexe simple.
Soit
 une fonction holomorphe sur
une fonction holomorphe sur  un ouvert convexe et
un ouvert convexe et  un point de
un point de  . La convexité permet d'affirmer que quels que soit
. La convexité permet d'affirmer que quels que soit  de
de  , les segments
, les segments ![\ [z_0;z], [z;z+h]](7/4d7d87b09914e05563f77cc5d594937a.png) sont inclus dans
sont inclus dans  , ainsi que le triangle de sommets
, ainsi que le triangle de sommets  .
.Soit la fonction sur
![\ V : F(z)= \int_{[z_0;z]} f(w) \,dw](d/08dbf9592fe3922f462f937395457e74.png)
 , l'intégrale curviligne de
, l'intégrale curviligne de  sur le triangle de sommets
sur le triangle de sommets  est nulle (lemme de Goursat énoncé pour les triangles), et donc
est nulle (lemme de Goursat énoncé pour les triangles), et donc ![\ F(z+h) - F(z) = \int_{[z;z+h]} f(w) \,dw = \int_{[0;h]} f(z+v) \,dv](f/7cf8da523ecb8e337613e8288ffc39f9.png)
Soit
![\ g_h : [0;h] \to \C, v \mapsto g_h(v)=f(z+v)-f(z), g_h](3/dc364b1db75bf043caf87ec641713daf.png) est continue et tend vers 0 lorsque | h | tend vers 0 :
est continue et tend vers 0 lorsque | h | tend vers 0 :![F(z+h) - F(z) = h.f(z) + \int_{[0;h]} g_h(v) \,dv = h.f(z) + h.sup\{g_h(v), v \in [0;h]\} = h.f(z) + o(h)](5/a95eab45f10a02f0ce5440245e3a67eb.png)
Donc
 est holomorphe en
est holomorphe en  avec
avec 
Deuxième partie
Soit
 une fonction holomorphe sur
une fonction holomorphe sur  un ouvert connexe simple et
un ouvert connexe simple et  un point de
un point de  .
.Pour tout
 dans
dans  , par définition de la connexité simple, tous les chemins de
, par définition de la connexité simple, tous les chemins de  entre
entre  et
et  sont homotopes, ce qui permet (car la valeur de l'intégrale d'une fonction holomorphe entre deux points ne dépend pas du chemin) de définir
sont homotopes, ce qui permet (car la valeur de l'intégrale d'une fonction holomorphe entre deux points ne dépend pas du chemin) de définir  , la fonction qui à un point de
, la fonction qui à un point de  associe la valeur de l'intégrale entre ce point et
associe la valeur de l'intégrale entre ce point et  :
:
Pour tout
 de
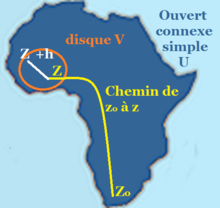
de  , comme
, comme  est ouvert, par définition il existe un réel
est ouvert, par définition il existe un réel  tel que le disque
tel que le disque  soit dans
soit dans  (sur l'illustration à droite, z n'est pas le centre du disque mais cela n'a pas d'importance). Un disque étant convexe, le problème va se ramener au cas précédent : la fonction
(sur l'illustration à droite, z n'est pas le centre du disque mais cela n'a pas d'importance). Un disque étant convexe, le problème va se ramener au cas précédent : la fonction  admet une primitive
admet une primitive  sur le disque
sur le disque  .
. tel que
tel que  , comme l'intégrale entre z0 et z + h ne dépend pas du chemin, on choisit la réunion d'un chemin (quelconque) entre z0 et z (à droite, en jaune) et du segment [z;z + h] (à droite en blanc), ce qui permet d'écrire :
, comme l'intégrale entre z0 et z + h ne dépend pas du chemin, on choisit la réunion d'un chemin (quelconque) entre z0 et z (à droite, en jaune) et du segment [z;z + h] (à droite en blanc), ce qui permet d'écrire :![F(z+h) = F(z) + \int_{[z;z+h]} f(w) \,dw = F(z) + G(z+h) - G(z)](c/cec06dc1db2cc337524695739efc33ba.png)
Donc
 admet une limite lorsque | h | tend vers 0.
admet une limite lorsque | h | tend vers 0.Conclusion :
 est holomorphe sur
est holomorphe sur  et
et  .
.Théorème intégral de Cauchy
Article détaillé : Théorème intégral de Cauchy.Théorème intégral de Cauchy — Soit Γ un lacet de
 , ce lacet est le bord d'une partie compacte connexe
, ce lacet est le bord d'une partie compacte connexe  de
de  . Soit
. Soit  une fonction holomorphe sur un ouvert
une fonction holomorphe sur un ouvert  contenant
contenant  , alors :
, alors :
Ce résultat reste valable si la fonction n'est pas holomorphe mais continue sur un nombre fini de points de l'ouvert

Ce théorème peut se démontrer de plusieurs manières :
- À partir de l'invariance de l'intégrale d'une fonction holomorphe le longs de chemins strictement homotopes.
- À partir de l'existence de primitives de fonction holomorphe sur un ouvert connexe, qu'on peut trouver à partir de l'ouvert
 .
. - À partir de la formule de Green Riemann.
Ce théorème est généralisé aux fonctions holomorphes sur un ouvert possédant des singularités par le théorème des résidus.
Formule intégrale de Cauchy
Article détaillé : Formule intégrale de Cauchy.Théorème — Soit
 une fonction holomorphe sur un ouvert
une fonction holomorphe sur un ouvert  de
de  , et
, et  une distance de
une distance de  .
.Alors
 est analytique sur
est analytique sur  , et
, et  , en notant
, en notant 

Avec 
où 
Par conséquent,
 est indéfiniment dérivable sur
est indéfiniment dérivable sur  , avec
, avec 
Remarques :
- Cette série, de Taylor en z0, converge sur tout disque ouvert de centre z0 et inclus dans U et peut converger sur un disque plus grand ; par exemple, la série de Taylor du logarithme converge sur tout disque ne contenant pas 0, même dans un voisinage des nombres réels strictement négatifs.
- De la formule intégrale de Cauchy, on déduit notamment que toute fonction holomorphe sur un ouvert contenant un disque fermé est complètement déterminée à l'intérieur de ce disque par ses valeurs sur la frontière de celui-ci (voir notamment ci dessous la propriété de la moyenne).
- Il y a équivalence entre holomorphie sur un ouvert et analyticité, l'analyticité impliquant clairement l'holomorphie.
- Le principe du prolongement analytique, le principe du maximum, le principe des zéros isolés, l'inégalité de Cauchy, le théorème de Liouville sont donc vérifiés par une fonction holomorphe.
Propriété de la moyenne
L'usage particulier de la formule ci dessus en z0 donne, suite à un changement de paramètre w = z0 + reiθ :

- L'intérêt de cette formule est dans le calcul numérique. Le calcul d'une intégrale est en effet plus stable que celui de dérivés.
- Ce résultat reste clairement valable pour la partie réelle et pour la partie imaginaire de f, qui sont des fonctions harmoniques. Comme une fonction harmonique est localement la partie réelle (ou imaginaire) d'une fonction holomorphe, les fonctions harmoniques vérifient le principe du maximum qui suit :
Principe du maximum
Soit
 une fonction holomorphe sur un ouvert connexe
une fonction holomorphe sur un ouvert connexe  .
.Si
 admet un maximum local en un point de
admet un maximum local en un point de  , alors
, alors  est constante.Démonstration
est constante.DémonstrationSi
 admet un maximum local en un point z0 de
admet un maximum local en un point z0 de  , et
, et  supposée non constante, alors, avec les notations précédentes :
supposée non constante, alors, avec les notations précédentes : , tel que
, tel que  tel que
tel que 
Avec la propriété de la moyenne :

Ce qui est absurde, donc
 est constante.
est constante.Développement de Laurent autour d'un point singulier
Article détaillé : Série de Laurent.Théorème — Soit
 une fonction holomorphe sur U − A avec U un ouvert connexe de
une fonction holomorphe sur U − A avec U un ouvert connexe de  et A l'ensemble des singularités isolées de
et A l'ensemble des singularités isolées de  dans U
dans UAlors, en chaque point
 de A,
de A,  admet,
admet,  , un développement de Laurent sur une couronne C(z0,R1,R2), où R2 > R1 > | z1 − z0 | et
, un développement de Laurent sur une couronne C(z0,R1,R2), où R2 > R1 > | z1 − z0 | et  (d désignant une distance de
(d désignant une distance de  ) :
) :
Avec 
où R1 < r < R2 Remarques :
- En particulier on peut prendre z1 = z0.
- le calcul des cn peut donner lieu à trois possibilités :
-
 : alors
: alors  peut se prolonger en une fonction analytique sur tous les points de A contenus dans le disque D(z0,R1), et ces points sont dits réguliers. Exemple d'une fonction présentant de tels coefficients :
peut se prolonger en une fonction analytique sur tous les points de A contenus dans le disque D(z0,R1), et ces points sont dits réguliers. Exemple d'une fonction présentant de tels coefficients :  en 0, 0 est un point régulier de
en 0, 0 est un point régulier de  .
.
-
 tel que
tel que  on ait
on ait  : alors la fonction
: alors la fonction  peut se prolonger en une fonction analytique sur tous les points de A contenus dans le disque D(z0,R1). Ce cas généralise en fait le premier. Ces points sont des pôles d'ordre au plus p de
peut se prolonger en une fonction analytique sur tous les points de A contenus dans le disque D(z0,R1). Ce cas généralise en fait le premier. Ces points sont des pôles d'ordre au plus p de  , il peut en exister qui sont réguliers (ordre 0). Exemples de fonctions présentant de tels coefficients :
, il peut en exister qui sont réguliers (ordre 0). Exemples de fonctions présentant de tels coefficients :  en 0 (0 est un pôle d'ordre k de
en 0 (0 est un pôle d'ordre k de  ), ou plus généralement les fonctions rationnelles en leurs pôles.
), ou plus généralement les fonctions rationnelles en leurs pôles.
-
- Dans les autres cas, il existe parmi les points de A contenus dans le disque D(z0,R1) au moins un point sur lequel il n'est pas possible de tenter un des prolongements ci dessus, un tel point est dit point singulier essentiel de f. Exemple :
 en 0, 0 est un point singulier essentiel de
en 0, 0 est un point singulier essentiel de  .
.
- Dans les autres cas, il existe parmi les points de A contenus dans le disque D(z0,R1) au moins un point sur lequel il n'est pas possible de tenter un des prolongements ci dessus, un tel point est dit point singulier essentiel de f. Exemple :
- ce théorème concerne en particulier les fonctions méromorphes.
- en pratique, ce développement s'effectue surtout en zéro.
- en pratique, dans le cas d'une fonction rationnelle qu'on cherche à développer en zéro, les coefficients cn se calculent via un classique développement en série en zéro des éléments simples.
- en pratique, le calcul des coefficients (en n'importe quel point) peut également s'effectuer grâce au théorème des résidus, souvent plus compliqué que de développer en série des fonctions rationnelles, mais qui reste en général plus simple que l'utilisation de la formule directe.
Applications :
Voir aussi
Notions importantes
- Différentielle
- Homotopie
- Connexité (mathématiques)
- Connexité simple
- Ensemble convexe
- Transformation conforme
Articles connexes
- Fonction méromorphe
- Fonction entière
- Fonction analytique
- Fonction harmonique
- Inégalité de Cauchy
- Théorème de Liouville (variable complexe)
- Théorème des résidus
Lien externe
Représentations graphiques de fonctions holomorphes, par Mikaël Mayer.
Wikimedia Foundation. 2010.