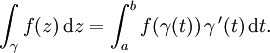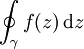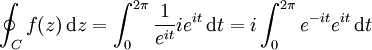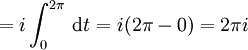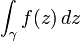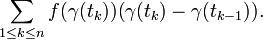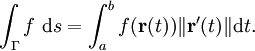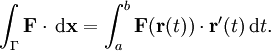Integrale curviligne

Intégrale curviligne

En mathématiques, l'intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe.

Sommaire

1 Analyse complexe
2 Analyse vectorielle
3 Voir aussi

Analyse complexe

L'intégrale curviligne est un des outils de base de l'analyse complexe. Si U est un ouvert du plan complexe, f une fonction continue de U dans C et γ un arc paramétré continûment dérivable tracé de [a,b] dans U on définit l'intégrale de f le long de γ en écrivant une intégrale de variable réelle

$\int_\gamma f(z)\,\mathrm{d}z = \int_a^b f(\gamma(t))\,\gamma\,'(t)\,\mathrm{d}t.$

Lorsque γ est une courbe fermée (ses deux extrémités coïncident) il arrive qu'on utilise la notation suivante

$\oint_\gamma f(z)\,\mathrm{d}z$

Exemple

Soit la fonction f(z)=1/z, et soit C le cercle unité parcouru une fois dans le sens trigonométrique, ce qui peut se paramétrer par e^it, avec t parcourant [0, 2π]. L'intégrale correspondante est

$\oint_C f(z)\,\mathrm{d}z = \int_0^{2\pi} {1\over e^{it}} ie^{it}\,\mathrm{d}t = i\int_0^{2\pi} e^{-it}e^{it}\,\mathrm{d}t$

$=i\int_0^{2\pi}\,\mathrm{d}t = i(2\pi-0)=2\pi i$

Extension aux arcs rectifiables

Plus généralement, si γ est un arc rectifiable, on peut définir l'intégrale curviligne

$\int_\gamma f(z)\,dz$

en introduisant une subdivision de segment [a,b] de la forme a = t₀ < t₁ < ... < t_n = b et en cherchant la limite des expressions de la forme

$\sum_{1 \le k \le n} f(\gamma(t_k)) ( \gamma(t_k) - \gamma(t_{k-1}) ).$

lorsque la subdivision a ses longueurs qui tendent vers 0.

Propriétés

Les propriétés fondamentales des intégrales curvilignes sont le théorème intégral de Cauchy et la formule intégrale de Cauchy, qui permettent d'établir le théorème des résidus.

Analyse vectorielle

Pour un champ scalaire 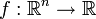$f:\mathbb{R}^n \rightarrow \mathbb{R}$ , l'intégrale curviligne le long de la courbe $Γ$ , paramétrée par $r (t)$ avec $t \in [a,b]$ est définie par :

$\int_\Gamma f\ \mathrm{d}s = \int_a^b f(\mathbf{r}(t)) \|\mathbf{r}'(t)\| \mathrm{d}t.$

De plus la longueur L de l'arc $Γ$ est donnée par:

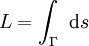$L = \int_\Gamma \ \mathrm{d}s$ .

De même pour un champ vectoriel 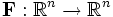$\mathbf{F} : \mathbb{R}^n \rightarrow \mathbb{R}^n$ la circulation le long de la courbe $Γ$ , paramétrée par $r (t)$ avec $t \in [a,b]$ est définie par :

$\int_\Gamma \mathbf{F}\cdot\,\mathrm{d}\mathbf{x} = \int_a^b \mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,\mathrm{d}t.$

Voir aussi

Portail des mathématiques

Ce document provient de « Int%C3%A9grale curviligne ».

Catégories : Analyse complexe | Analyse vectorielle | Théorie de l'intégration

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Integrale curviligne de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Intégrale Curviligne — En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
Intégrale curviligne — En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
intégrale curviligne — kreivinis integralas statusas T sritis fizika atitikmenys: angl. curvilinear integral; path integral vok. Kurvenintegral, n rus. криволинейный интеграл, m pranc. intégrale curviligne, f … Fizikos terminų žodynas
curviligne — [ kyrviliɲ ] adj. • 1613; de curvi et ligne; remplace courbeline (XVIe) ♦ Math. Qui est formé par des lignes courbes. ⇒ arrondi, courbe, incurvé. Polygone curviligne. Angle curviligne. ♢ Abscisse curviligne : longueur d un arc de courbe orientée … Encyclopédie Universelle
Integrale de chemin — Intégrale de chemin Une intégrale de chemin («path integral» en anglais) est une intégrale fonctionnelle, c est à dire que l intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes)… … Wikipédia en Français
Intégrale De Chemin — Une intégrale de chemin («path integral» en anglais) est une intégrale fonctionnelle, c est à dire que l intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes) comme pour les… … Wikipédia en Français
Integrale de surface — Intégrale de surface En mathématiques, une intégrale de surface est une intégrale définie sur toute une surface qui peut être courbe dans l espace. Pour une surface donnée, on peut intégrer sur un champ scalaire ou sur un champ vectoriel. Les… … Wikipédia en Français
Intégrale De Surface — En mathématiques, une intégrale de surface est une intégrale définie sur toute une surface qui peut être courbe dans l espace. Pour une surface donnée, on peut intégrer sur un champ scalaire ou sur un champ vectoriel. Les intégrales de surface… … Wikipédia en Français
Intégrale de chemin — Une intégrale de chemin (« path integral » en anglais) est une intégrale fonctionnelle, c est à dire que l intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes) comme… … Wikipédia en Français
Curviligne — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Curviligne », sur le Wiktionnaire (dictionnaire universel) Coordonnées curvilignes Intégrale… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Integrale curviligne

Intégrale curviligne

Sommaire