Green Riemann

Green Riemann

Théorème de Green

Articles d'analyse vectorielle
Champ vectorielChamp scalaire
Objets d'étude
Champ vectoriel Champ scalaire
Équation aux dérivées partielles
de Laplace de Poisson
Opérateurs
Nabla Gradient
Rotationnel Divergence
Laplacien scalaire Bilaplacien
Laplacien vectoriel D'alembertien
Théorèmes
de Green de Stokes
de Helmholtz de flux-divergence
du gradient du rotationnel

En mathématiques, le théorème de Green, ou théorème de Green-Riemann donne la relation entre une intégrale curviligne autour d'une courbe simple fermée C et l'intégrale double sur la région du plan D délimitée par C.

Ce théorème est nommé d'après le scientifique George Green et se base sur le théorème de Stokes. À ne pas confondre avec le théorème de Green-Ostrogradski, ou théorème de flux-divergence.

Sommaire

Énoncé

Domaine délimité par une courbe régulière par morceaux.

Théorème de Green — Soit C, une courbe plane simple, positivement orientée et C1 par morceaux, D le domaine compact lisse du plan délimité par C et Pdx + Qdy une 1-forme différentielle sur 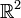\R^2. Si P et Q ont des dérivées partielles continues sur une région ouverte incluant D, alors :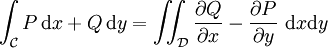

\int_\mathcal{C} P\,\mathrm dx + Q\,\mathrm dy = \iint_\mathcal{D} \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\ \mathrm dx\mathrm dy

Notation alternative

Il existe une autre façon de noter ce théorème, qui se rapproche de celle utilisée pour le théorème de Stokes. On se place sur un domaine compact lisse du plan Ω, de bord ∂Ω, en notant la forme différentielle ω. Alors la dérivée extérieure de ω s'écrit :

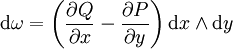
\mathrm d\omega = \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \mathrm dx \wedge \mathrm dy

On peut alors résumer le théorème de Green par la formule :

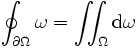
\oint_{\partial \Omega} \omega = \iint_{\Omega} \mathrm d\omega

Le cercle sur l'intégrale précise que le bord décrit une courbe fermée. En dessinant une flèche dessus, on définit l'orientation — positive ou négative.

Utilisations

Le théorème de Green permet notamment de démontrer l'inégalité de Poincaré, ainsi que le théorème intégral de Cauchy pour les fonctions holomorphes.

Calculs d'aires

L'utilisation du théorème de Green permet de calculer l'aire délimitée par une courbe paramétrée fermée. Cette méthode est concrètement appliquée dans les planimètres.

Soit D un domaine du plan auquel le théorème de Green s'applique et soit 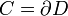C = \partial D sa frontière, orientée positivement par rapport à D. On a :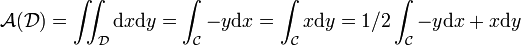

\mathcal{A(D)} = \iint_\mathcal{D} \mathrm dx \mathrm dy = \int_\mathcal{C} -y \mathrm dx = \int_\mathcal{C} x \mathrm dy = 1/2 \int_\mathcal{C} -y \mathrm dx + x \mathrm dy

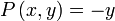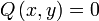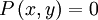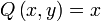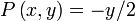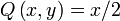en prenant respectivement P \left( x, y \right) = -y et Q \left( x, y \right) = 0, ou bien P \left( x, y \right) = 0 et Q \left( x, y \right) = x, ou enfin P \left( x, y \right) = -y/2 et Q \left( x, y \right) = x/2.

On traite ici l'exemple du disque unité D, dont le bord est le cercle unité C paramétré par :

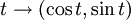
t \to \left( \cos{t}, \sin{t} \right)

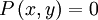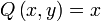et de longueur 2π. En prenant par exemple P \left( x, y \right) = 0 et Q \left( x, y \right) = x , on obtient :

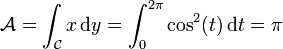\mathcal{A} = \int_\mathcal{C} x\,\mathrm dy = \int_{0}^{2\pi} \cos^2 (t)\,\mathrm dt = \pi .

On a ainsi montré que l'aire du disque unité est π.

  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Th%C3%A9or%C3%A8me de Green ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Green Riemann de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Formule de Green-Riemann — Théorème de Green Articles d analyse vectorielle Objets …   Wikipédia en Français

  • Théorème de Green-Riemann — Théorème de Green Articles d analyse vectorielle Objets …   Wikipédia en Français

  • Théorème de Green Riemann — Théorème de Green Articles d analyse vectorielle Objets …   Wikipédia en Français

  • GREEN (G.) — GREEN GEORGE (1793 1841) Mathématicien anglais, né et mort à Sneinton (près de Nottingham). George Green, à travers sa recherche d’une formulation mathématique de la théorie de l’électricité statique et du magnétisme, est le créateur de la… …   Encyclopédie Universelle

  • Théorème de green — Articles d analyse vectorielle Objets …   Wikipédia en Français

  • Théorème de Green — En mathématiques, le théorème de Green, ou théorème de Green Riemann donne la relation entre une intégrale curviligne autour d une courbe simple fermée C et l intégrale double sur la région du plan D délimitée par C. Ce théorème est nommé d après …   Wikipédia en Français

  • Cauchy-Riemann equations — In mathematics, the Cauchy Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, are two partial differential equations which provide a necessary and sufficient condition for a differentiable… …   Wikipedia

  • Fonction De Green — On appelle fonction de Green en physique ce que les mathématiciens appellent solution élémentaire d une équation différentielle linéaire à coefficients constants, ou d une équation aux dérivées partielles linéaire à coefficients constants. Ces… …   Wikipédia en Français

  • Fonction de Green — On appelle fonction de Green en physique ce que les mathématiciens appellent solution élémentaire ou fondamentale d une équation différentielle linéaire à coefficients constants, ou d une équation aux dérivées partielles linéaire à coefficients… …   Wikipédia en Français

  • Fonction de green — On appelle fonction de Green en physique ce que les mathématiciens appellent solution élémentaire d une équation différentielle linéaire à coefficients constants, ou d une équation aux dérivées partielles linéaire à coefficients constants. Ces… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”