- Transformation conforme
-
En mathématiques, et plus précisément en géométrie et en analyse complexe, une transformation conforme est une transformation qui conserve les angles.


Une France conforme, et... anticonformeSommaire
Cas du plan
Une transformation conforme dans le plan est une transformation d'un domaine du plan dans un plan, cette transformation conservant les angles entre deux courbes orientées. Autrement dit, c'est localement une similitude directe.
Si la transformation fait correspondre un point M à un point m, elle peut s'interpréter dans le plan complexe comme une relation Z = f(z) entre les affixes de ces deux points. Lorsque la fonction f est analytique, la transformation est conforme. Cette remarque a été utilisée, en particulier pour calculer simplement des écoulements autour d'un profil d'aile, en utilisant une transformation qui fait passer d'un cercle au profil voulu.
Les transformations qui inversent les angles sont dites anticonformes ; ce sont les composées des précédentes par les réflexions.
Exemples holomorphes
Aux coordonnées cartésiennes (x,y) d'un point du plan, on préfère la notation
 du plan complexe. En effet, on peut non seulement ajouter les vecteurs (ou points) du plan mais également les multiplier. La multiplication par un nombre réel r correspond à une homothétie, celle par un nombre unitaire eiθ à une rotation d'angle θ et celle par un nombre complexe quelconque
du plan complexe. En effet, on peut non seulement ajouter les vecteurs (ou points) du plan mais également les multiplier. La multiplication par un nombre réel r correspond à une homothétie, celle par un nombre unitaire eiθ à une rotation d'angle θ et celle par un nombre complexe quelconque  correspond à une similitude. Les similitudes sont clairement des transformations conformes.
correspond à une similitude. Les similitudes sont clairement des transformations conformes.Une fonction holomorphe (ou analytique) est localement une similitude
 avec a = f'(z0) la dérivée et b = f(z0) la valeur de f en z0. La dérivée est le facteur de zoom de cette transformation. Elle est donc une transformation conforme là où sa dérivée ne s'annule pas. Aux zéros de la dérivée, l'application n'est pas conforme et ressemble localement à un monôme:
avec a = f'(z0) la dérivée et b = f(z0) la valeur de f en z0. La dérivée est le facteur de zoom de cette transformation. Elle est donc une transformation conforme là où sa dérivée ne s'annule pas. Aux zéros de la dérivée, l'application n'est pas conforme et ressemble localement à un monôme:Les monômes
 sont les fonctions holomorphes les plus simples, après les similitudes qui sont de dérivée constante. Un problème pour les représenter est qu'une fonction holomorphe n'est en général pas injective: Pour le monôme zk par exemple k points différents sont envoyés sur la même valeur à part 0 où la dérivée est nulle et où l'application n'est pas conforme car les angles en 0 sont multipliés par k. On dit qu'il est de multiplicité k.
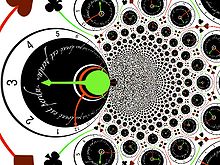
sont les fonctions holomorphes les plus simples, après les similitudes qui sont de dérivée constante. Un problème pour les représenter est qu'une fonction holomorphe n'est en général pas injective: Pour le monôme zk par exemple k points différents sont envoyés sur la même valeur à part 0 où la dérivée est nulle et où l'application n'est pas conforme car les angles en 0 sont multipliés par k. On dit qu'il est de multiplicité k.Si on considère le plan pavé par l'image d'une horloge, sa mise au carré sera:

Le disque central est envoyé sur lui-même mais chaque point (sauf zéro) est recouvert deux fois, ce qui rend l'image illisible. Par exemple +1 (à 3h) et -1 (à 9h) sont envoyés sur +1 (à droite de l'image au milieu), +i (midi) et -i (6h) sont envoyés sur -1 (9h).
Une somme de monômes est un polynôme. Son monôme de plus haut degré détermine son degré: Chaque point complexe est atteint le même nombre de fois (en comptant les multiplicités).
Pour avoir une application injective, on peut se restreindre par exemple soit au demi-plan de parties réelles positives soit à l'autre demi-plan des parties réelles négatives
En prenant de la distance, le même effet opère sur le plan entier.
Image réciproque
On peut plutôt considérer non pas l'image directe par une application, mais plutôt l'image réciproque (aussi parfois appelée le tiré en arrière, traduction de pullback):
On place l'image non pas dans l'espace de départ mais plutôt dans l'espace d'arrivée et on colore le point z par la couleur du pixel f(z).
Remarquez la duplication : les points z et -z sont envoyés tous deux sur la même image z².
De même, le monôme d'ordre k envoie k points à la même image.
On comprend de nombreuses informations concernant l'application conforme en visualisant le tiré en arrière d'une image. Comme le facteur de zoom de l'image directe est la dérivée de la fonction, c'est donc son inverse en ce qui concerne l'image réciproque. On remarque en particulier les zéros de la dérivée où le facteur de zoom devient donc infini. On remarque également quand la dérivée est réelle positive, là où l'image ne subit qu'une dilatation, et quand la dérivée est réelle négative, là où l'image est "la tête en bas".
Inversion, pôles
Après les fonctions holomorphes dont on visualise la dérivée, on comprend également, dans le cadre plus général des fonctions méromorphes, la position et l'ordre des pôles.
L'inversion
 possède un pôle simple en zéro. C'est une transformation de Möbius
possède un pôle simple en zéro. C'est une transformation de Möbius  avec a, b, c et d quatre complexes tels que
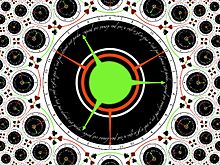
avec a, b, c et d quatre complexes tels que  et elle envoie cercles et droites sur cercles et droites. En particulier les horizontales et verticales deviennent des cercles passant par zéro. L'inversion échange l'intérieur et l'extérieur du disque unité.
et elle envoie cercles et droites sur cercles et droites. En particulier les horizontales et verticales deviennent des cercles passant par zéro. L'inversion échange l'intérieur et l'extérieur du disque unité.Comme les zéros, les pôles peuvent ne pas être simples mais d'ordre plus élevé. À part les cercles centrés en la singularité (et encore si elle est unique), les autres cercles ne sont plus conservés qu'au niveau infinitésimal. On peut voir un pôle double comme la limite quand deux pôles simples se rapprochent.
Logarithme et exponentielle
Une application très importante en analyse complexe et en cartographie est la transformation de coordonnées cartésiennes (x,y) en coordonnées polaires (r,θ). Cette transformation est réalisée par le couple de fonctions logarithme/exponentielle réciproques l'une de l'autre (log(exp(z)) = z). En effet,
 transforme (r,θ) en (x=log(r), y=θ) et
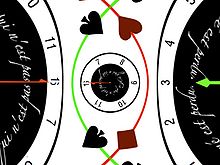
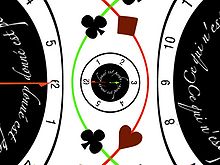
transforme (r,θ) en (x=log(r), y=θ) et  transforme (x,y) en (r=exp(x),θ=y). En images, le logarithme déroule les cercles centrés en l'origine en droites verticales et des rayons en droites horizontales. L'exponentielle au contraire, enroule les droites verticales en cercles concentriques et les droites horizontales en rayons passant par l'origine. Remarquez que le logarithme va vers l'infini en zéro mais beaucoup plus lentement que l'inversion.
transforme (x,y) en (r=exp(x),θ=y). En images, le logarithme déroule les cercles centrés en l'origine en droites verticales et des rayons en droites horizontales. L'exponentielle au contraire, enroule les droites verticales en cercles concentriques et les droites horizontales en rayons passant par l'origine. Remarquez que le logarithme va vers l'infini en zéro mais beaucoup plus lentement que l'inversion.En changeant le pas du réseau, on obtient des variations en spirales du plus bel effet. Comme les pôles et les zéros, on peut les ajouter.
Singularité essentielle
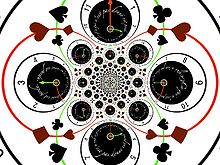
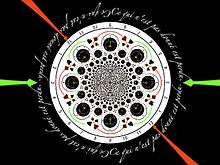
Les fonctions analytiques souffrent encore d'autres types de singularités. La singularité essentielle
 par exemple est nulle pour z = 0 − , avec accumulation de zéros, et indéterminée pour z = 0 + avec accumulation de pôles.
par exemple est nulle pour z = 0 − , avec accumulation de zéros, et indéterminée pour z = 0 + avec accumulation de pôles.Rayon de convergence
Les fonctions méromorphes sont développables en série entière ; leur série de Taylor admet un rayon de convergence non nul. La comparaison des tirés en arrière de la fonction et de sa série de Taylor, tronquée à un certain ordre, permet de comprendre visuellement cette notion :
Cas de la dimension n ≥ 3
Les transformations conformes sont les difféomorphismes dont la jacobienne est une similitude ; Liouville a démontré que, contrairement au cas du plan, les seules transformations conformes en dimension n ≥ 3 sont les produits d'inversions et de similitudes, c'est-à-dire les transformations conservant l'ensemble des hypersphères et des hyperplans.
Applications pratiques
Mécanique des fluides
Au début de l'aérodynamique la transformation conforme a fourni, sous l'hypothèse d'un écoulement irrotationnel d'un fluide supposé incompressible et parfait (voir Mécanique des fluides), une méthode élégante de calcul de l'écoulement bi-dimensionnel autour d'un profil d'aile et de sa portance. Certaines transformations bien choisies permettent en effet de transformer un cercle en une courbe ressemblant à un profil d'aile et en déduire la portance d'une aile de grand allongement.
La première application de cette technique correspond à ce qu'on appelle la transformation de Joukovsky :

Cette équation simple conduit à un profil qui présente des inconvénients, en particulier parce que le bord de fuite d'un tel profil possède un point de rebroussement, ce qui met en cause sa réalisation pratique.
Cartographie
Certaines projections cartographiques sont conformes. Citons par exemple la projection stéréographique (plane), la projection de Mercator et sa généralisation (cylindriques), et la projection de Lambert (conique).
Article connexe
Catégories :- Transformation géométrique
- Méthode mathématique de la physique
- Analyse complexe
Wikimedia Foundation. 2010.







 .
.
 .
.

 .
.
 . Remarquez les invariances par homothétie et rotation qui correspondent à les invariances par translations horizontales, resp. verticales du réseau.
. Remarquez les invariances par homothétie et rotation qui correspondent à les invariances par translations horizontales, resp. verticales du réseau.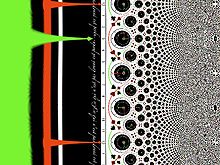
 . Remarquez que le disque unité déroulé se répète verticalement.
. Remarquez que le disque unité déroulé se répète verticalement.