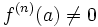- Zero d'une fonction holomorphe
-
Zéro d'une fonction holomorphe
En analyse complexe, on appelle zéro d'une fonction analytique ou holomorphe f un nombre complexe a tel que f(a) = 0.
Sommaire
Ordre de multiplicité d'un zéro isolé
Soient
 un ouvert (non vide) de
un ouvert (non vide) de 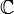 et une fonction analytique
et une fonction analytique  .
.On considère un zéro
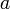 de
de  . Il existe un disque ouvert
. Il existe un disque ouvert 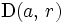 inclus dans
inclus dans  où
où  se développe en série entière (de rayon de convergence au moins égal à
se développe en série entière (de rayon de convergence au moins égal à 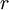 ):
):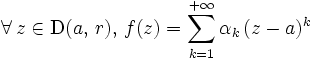 (le terme constant est
(le terme constant est 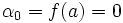 ).
).
Deux cas (seulement) sont possibles :
- Si pour tout
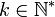 ,
, 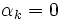 , alors
, alors
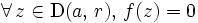 :
:  est identiquement nulle sur
est identiquement nulle sur 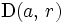 ;
; 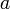 est donc dans ce cas un zéro non isolé.
est donc dans ce cas un zéro non isolé.
- Dans le cas contraire, soit
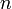 l'indice du premier coefficient non nul de la série entière (
l'indice du premier coefficient non nul de la série entière (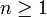 et
et 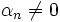 ) : on peut écrire
) : on peut écrire
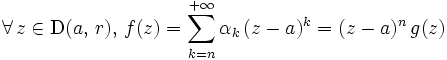 , où
, où
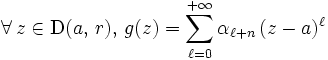
- La fonction
 ainsi définie est analytique et
ainsi définie est analytique et  .
. - Par continuité de
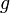 en
en 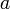 :
: - il existe un réel strictement positif
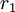 tel que
tel que 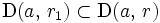 et tel que
et tel que 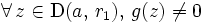 .
. - Finalement :
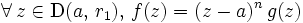 et
et 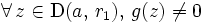 .
.- On en déduit que
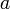 est le seul point de
est le seul point de 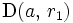 où
où  s'annule ;
s'annule ; 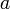 est donc dans ce cas un zéro isolé.
est donc dans ce cas un zéro isolé.
On peut alors énoncer :
Théorème et définition
Un élément
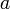 de
de  est un zéro isolé de la fonction analytique
est un zéro isolé de la fonction analytique  si et seulement s'il existe :
si et seulement s'il existe :- un entier
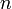 strictement positif
strictement positif - un disque ouvert
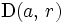 inclus dans
inclus dans 
- une fonction analytique
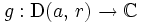 telle que
telle que 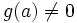 et
et 
Dans ce cas, l'entier (unique)
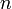 est appelé ordre de multiplicité (ou multiplicité) du zéro isolé
est appelé ordre de multiplicité (ou multiplicité) du zéro isolé 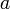 .
.
Lorsque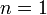 , on dit que
, on dit que 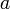 est un zéro simple.
est un zéro simple.Remarque
- L'ordre de multiplicité n'est défini que pour les zéros isolés d'une fonction analytique.
- On définit en algèbre la notion analogue d'ordre de multiplicité d'une racine d'un polynôme non nul, dont celle qui vient d'être définie constitue une généralisation.
Compte tenu de ce que (avec les notations déjà utilisées)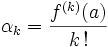 pour tout
pour tout  et de ce que l'ordre de multiplicité d'un zéro isolé
et de ce que l'ordre de multiplicité d'un zéro isolé 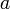 est l'indice du premier coefficient non nul du développement de
est l'indice du premier coefficient non nul du développement de  en série entière au voisinage de
en série entière au voisinage de 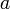 , on peut donner la caractérisation suivante de l'ordre de multiplicité :
, on peut donner la caractérisation suivante de l'ordre de multiplicité :Propriété
Soient
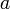 un élément de
un élément de  et
et 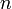 un entier naturel non nul.
un entier naturel non nul.
Pour que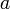 soit un zéro isolé d'ordre
soit un zéro isolé d'ordre 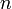 de la fonction analytique
de la fonction analytique  , il faut et il suffit que :
, il faut et il suffit que :- pour tout entier
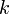 tel que
tel que 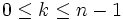 ,
, 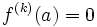
- et
Exemple
Soient
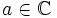 et
et 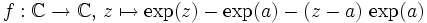 . Cette fonction est entière (c'est-à-dire holomorphe sur
. Cette fonction est entière (c'est-à-dire holomorphe sur 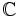 ) et
) et 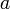 en est un zéro isolé d'ordre 2.
en est un zéro isolé d'ordre 2.On vérifie en effet que
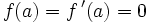 et
et 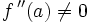 .
.Applications
Soient
 un ouvert de
un ouvert de 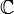 et une fonction analytique
et une fonction analytique  .
.- Compte tenu de la caractérisation des zéros isolés par les dérivées successives, on peut affirmer : pour qu'un zéro
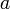 de
de  soit non isolé, il faut et il suffit que
soit non isolé, il faut et il suffit que 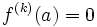 pour tout
pour tout  .
. - L'étude faite plus haut a montré la propriété suivante :
Principe des zéros isolés
Si
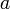 est un zéro non isolé de la fonction analytique
est un zéro non isolé de la fonction analytique  , alors il existe un disque ouvert
, alors il existe un disque ouvert 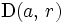 inclus dans
inclus dans  sur lequel
sur lequel  est nulle.
est nulle.
On en déduit lePrincipe du prolongement analytique
Soient
 un ouvert connexe de
un ouvert connexe de 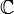 et deux fonctions
et deux fonctions  analytiques sur
analytiques sur  .
.
S'il existe dans l'ensemble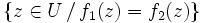 au moins un point
au moins un point 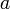 non isolé, alors
non isolé, alors 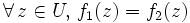 .
.
On l'énonce souvent sous la forme suivante :Soient
 un ouvert connexe de
un ouvert connexe de 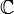 , deux fonctions
, deux fonctions  analytiques sur
analytiques sur  et
et 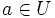 .
.
S'il existe une suite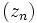 à termes dans
à termes dans  , convergeant vers
, convergeant vers 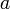 , telle que pour tout
, telle que pour tout 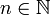 ,
, 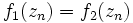 ,
,
alors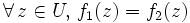 .
.
On peut interpréter ainsi ce théorème : si deux fonctions analytiques sur un ouvert connexe prennent les mêmes valeurs sur un sous-ensemble dont certains points sont assez "resserrés", alors elles sont égales.Démonstration
Soit
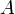 l'ensemble des zéros non isolés de la fonction analytique
l'ensemble des zéros non isolés de la fonction analytique 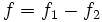 :
:- c'est un sous-ensemble non vide de
 , car
, car 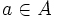
- il est fermé. En effet d'après 1.,
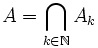 , où pour tout
, où pour tout  ,
, 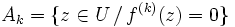 ; chaque
; chaque 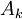 est fermé (image réciproque du fermé {0} par la fonction continue
est fermé (image réciproque du fermé {0} par la fonction continue 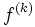 ), donc
), donc 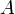 est une intersection de fermés ;
est une intersection de fermés ; - il est ouvert. En effet, si
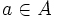 , il existe (principe des zéros isolés) un disque ouvert
, il existe (principe des zéros isolés) un disque ouvert 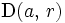 inclus dans
inclus dans  sur lequel
sur lequel  est nulle : tous les points de ce disque sont donc des zéros non isolés de
est nulle : tous les points de ce disque sont donc des zéros non isolés de  , ce qui prouve que
, ce qui prouve que 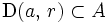 ;
; - comme
 est connexe, il résulte des 3 points précédents que
est connexe, il résulte des 3 points précédents que 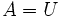 , donc
, donc  est nulle sur
est nulle sur  , autrement dit,
, autrement dit, 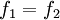 .
.
Exemple
Soit
 un ouvert connexe de
un ouvert connexe de 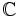 contenant un intervalle
contenant un intervalle 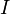 de
de 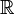 non réduit à un point : les points de
non réduit à un point : les points de 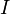 sont non isolés.
sont non isolés.
Si les fonctions sont analytiques sur
sont analytiques sur  et telles que pour tout
et telles que pour tout 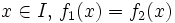 , alors
, alors 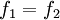 ;
;
autrement dit, pour tout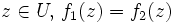 .
.Cela signifie qu'une fonction
 admet au plus un prolongement analytique à un ouvert connexe
admet au plus un prolongement analytique à un ouvert connexe  de
de 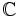 contenant
contenant 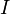 .
.- Ainsi, la fonction exponentielle complexe est le seul prolongement analytique à
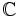 de la fonction exponentielle réelle.
de la fonction exponentielle réelle. - On suppose connue l'identité
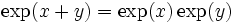 pour tout couple de réels. On peut l'étendre par prolongement analytique à un couple quelconque de nombres complexes. En effet :
pour tout couple de réels. On peut l'étendre par prolongement analytique à un couple quelconque de nombres complexes. En effet :
- Soit
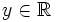 (quelconque). On définit sur
(quelconque). On définit sur 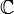 (ouvert connexe) deux fonctions analytiques
(ouvert connexe) deux fonctions analytiques  en posant
en posant 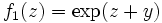 et
et 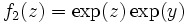 . Pour tout
. Pour tout 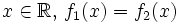 , donc (principe du prolongement analytique), pour tout
, donc (principe du prolongement analytique), pour tout 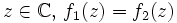 , ou
, ou 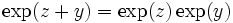 .
. - Ceci prouve : quels que soient
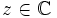 et
et 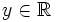 ,
, 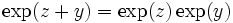 .
. - Soit
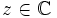 (quelconque). On définit sur
(quelconque). On définit sur 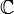 (ouvert connexe) deux fonctions analytiques
(ouvert connexe) deux fonctions analytiques 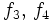 en posant
en posant 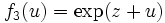 et
et 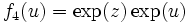 . Pour tout
. Pour tout 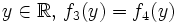 (voir supra), donc (principe du prolongement analytique), pour tout
(voir supra), donc (principe du prolongement analytique), pour tout 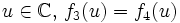 , ou
, ou 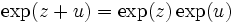 .
. - Ceci prouve : quels que soient
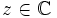 et
et 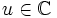 ,
, 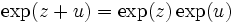 .
.
- Soit
Voir aussi
- Portail des mathématiques
Catégories : Analyse complexe | Zéro
Wikimedia Foundation. 2010.