Operateur differentiel

Operateur differentiel: Opérateur différentiel

Un opérateur différentiel est un opérateur agissant sur des fonctions différentiables.

Lorsque la fonction est à une seule variable, l'opérateur différentiel est construit à partir des dérivées ordinaires.

Lorsque la fonction est à plusieurs variables, l'opérateur différentiel est construit à partir des dérivées partielles.

Sommaire

1 Notations

1.1 Dérivées du premier ordre

1.2 Dérivées d'ordres plus élevés

2 Définition d'un opérateur différentiel

2.1 Définition

2.2 Propriété de localité

3 Transformée de Fourier

3.1 Introduction de la transformée de Fourier

3.2 Application aux opérateurs différentiels

3.3 Symbole d'un opérateur différentiel

3.4 Symbole principal d'un opérateur différentiel

4 Classification des opérateurs différentiels

4.1 Opérateur elliptique

4.2 Opérateur hyperbolique

5 Exemples importants pour la physique théorique

5.1 Opérateur laplacien

5.2 Opérateur d'alembertien

5.3 Opérateur de la chaleur

6 Opérateur différentiel à coefficients constants

7 Cas général

7.1 Expression de la transformée de Fourier

8 Voir aussi

9 Bibliographie

Notations

Soit $Ω$ un ouvert de 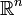$\R^n$ , et $x$ un point de $Ω$ . On introduit les $n$ coordonnées $x k (k = 1,..., n)$ . Supposons que l'on ait une fonction des $n$ variables : $x k$ .

Dérivées du premier ordre

Pour simplifier les écritures, on note usuellement la dérivée partielle première par rapport à la coordonnée $x k$ par le symbole :
$\partial_k \ = \ \frac{\partial ~~}{\partial x_k}$
On est également amené à introduire l'opérateur différentiel $D k$ du premier ordre défini par :
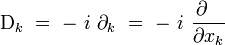
$\mathrm D_k \ = \ - \ i \ \partial_k \ = \ - \ i \ \frac{\partial ~~}{\partial x_k}$
Dans cette définition, $i$ est la « racine de l'unité » complexe : $i 2 = - 1$ . L'intérêt de définir cet opérateur $D k$ apparaitra plus tard, en relation avec la transformée de Fourier.

On utilise les notations sous forme de multi-indices : un multi-indice $α$ est un $n$ -uplet d'entiers
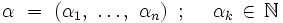
$\alpha \ = \ \left( \alpha_1, \ \dots, \ \alpha_n \right) \ ; \quad \ \alpha_k \, \in \, \mathbb{N}$
Sa longueur $| α |$ est définie comme la somme des $α i$ et on définit enfin la multi-factorielle :
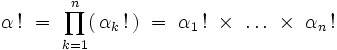
$\alpha \, ! \ = \ \prod_{k=1}^n ( \, \alpha_k \, ! \, ) \ = \ \alpha_1 \, ! \ \times \ \dots \ \times \ \alpha_n \, !$
Dérivées d'ordres plus élevés

La dérivée partielle d'ordre $α k$ par rapport à la coordonnée $x k$ correspond au symbole : $\partial^{\alpha_k}_k$

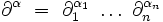
On définit alors les dérivées partielles, d'ordre global $| α |$ : $\partial^{\alpha} \ = \ \partial^{\alpha_1}_1 \ \dots \ \partial^{\alpha_n}_n$

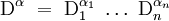
Et les opérateurs différentiels $D α$ , d'ordre global $| α |$ : $\mathrm D^{\alpha} \ = \ \mathrm D^{\alpha_1}_1 \ \dots \ \mathrm D^{\alpha_n}_n$

Définition d'un opérateur différentiel

Définition

Un opérateur différentiel linéaire d'ordre $m$ est défini par :
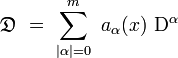
$\mathfrak{D} \ = \ \sum_{|\alpha| = 0}^m \ a_{\alpha}(x) \ \mathrm D^{\alpha}$
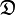où les $a α (x)$ sont des fonctions de $n$ variables, appelées coefficents de l'opérateur $\mathfrak{D}$ .

Propriété de localité

Un opérateur différentiel 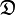$\mathfrak{D}$ est local au sens où, pour déterminer ses effets 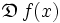$\mathfrak{D} \, f(x)$ sur une fonction $f (x)$ suffisamment différentiable, seule la connaissance de la fonction dans le voisinage du point $x$ est nécessaire.

Transformée de Fourier

Introduction de la transformée de Fourier

On définit ici la transformée de Fourier de la fonction $f (x)$ de $n$ variables $x k (k = 1,..., n)$ par :
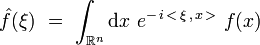
$\hat{f}(\xi) \ = \ \int_{\mathbb{R}^n} \mathrm dx \ e^{- \, i \, < \, \xi \, , \, x \, >} \ f(x)$
Dans cette définition :

on note $ξ$ le $n$ -uplet constitué des variables : $ξ k (k = 1,..., n)$ .

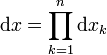la mesure est : $\mathrm dx = \prod_{k=1}^{n} \mathrm dx_k$ .

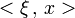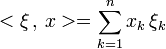le facteur $<\xi \, , \, x>$ dans l'exponentielle oscillante désigne le produit scalaire : $<\xi \, , \, x> = \sum_{k=1}^{n} x_k \, \xi_k$ .

La formule de transformation inverse s'écrit alors :
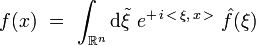
$f(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi , \, x \, >} \ \hat{f}(\xi)$
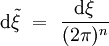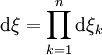où la mesure est : $\mathrm d \tilde{\xi} \ = \ \frac{\mathrm d \xi}{(2\pi)^n} \quad$ avec $\mathrm d\xi = \prod_{k=1}^{n} \mathrm d\xi_k$ .

Application aux opérateurs différentiels

Appliquons l'opérateur différentiel $\mathrm D_k = - \, i \, \partial_k$ à la représentation de Fourier de la fonction $f (x)$ . En supposant qu'on puisse intervertir la dérivation et l'intégration, on obtient :
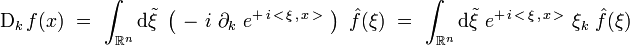
$\mathrm D_k \, f(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ \left( \ - \ i \ \partial_k \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \right) \ \hat{f}(\xi) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \xi_k \ \hat{f}(\xi)$
qu'on peut écrire : 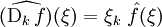$(\widehat{\mathrm D_k \, f})(\xi) = \xi_k \ \hat{f}(\xi)$ . On en déduit que :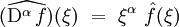
$(\widehat{\mathrm D^{\alpha} \, f})(\xi) \ = \ \xi^{\alpha} \ \hat{f}(\xi)$
où : 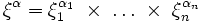$\xi^{\alpha} = \xi_1^{\alpha_1} \ \times \ \dots \ \times \ \xi_n^{\alpha_n}$ . L'opérateur différentiel 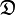$\mathfrak{D}$ d'ordre $m$ vérifie donc la relation :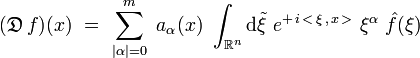
$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ a_{\alpha}(x) \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \xi^{\alpha} \ \hat{f}(\xi)$
On peut intervertir la somme et l'intégrale pour écrire :
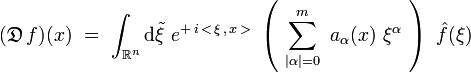
$(\mathfrak{D} \,f)(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \left( \ \sum_{|\alpha| = 0}^m \ a_{\alpha}(x) \ \xi^{\alpha} \ \right) \ \hat{f}(\xi)$
Symbole d'un opérateur différentiel

On appelle symbole de l'opérateur différentiel 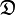$\mathfrak{D}$ d'ordre $m$ la fonction $σ(x,ξ)$ des $2 n$ variables $(x,ξ)$ polynomiale en $ξ$ de degré $m$ :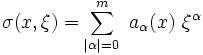
$\sigma (x,\xi) = \sum_{|\alpha| = 0}^m \ a_{\alpha}(x) \ \xi^{\alpha}$
de telle sorte que :
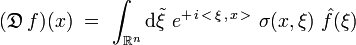
$(\mathfrak{D} \,f)(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \sigma (x,\xi) \ \hat{f}(\xi)$
On constate que cette formule pourrait en fait permettre de définir l'opérateur 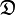$\mathfrak{D}$ à partir de son symbole $σ$ . Cette idée sera mise à profit dans la théorie des opérateurs pseudo-différentiels.

Attention : pour un opérateur différentiel dont les coefficients $a α (x)$ ne sont pas constants, le symbole $σ(x,ξ)$ dépend des coordonnées d'espace $x$ , et l'expression 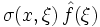$\sigma(x,\xi) \, \hat{f}(\xi)$ n'est pas la transformée de Fourier de $(\mathfrak{D} \, f)(x)$ , c’est-à-dire que :
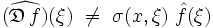
$(\widehat{\mathfrak{D} \, f})(\xi) \ \ne \ \sigma (x,\xi) \ \hat{f}(\xi)$
La formule correcte de la transformée de Fourier est calculée dans le paragraphe « Cas général ».

Symbole principal d'un opérateur différentiel

On appelle symbole principal de l'opérateur différentiel 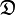$\mathfrak{D}$ d'ordre $m$ la fonction :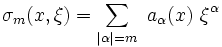
$\sigma_m (x,\xi) = \sum_{|\alpha| = m} \ a_{\alpha}(x) \ \xi^{\alpha}$
Classification des opérateurs différentiels

Opérateur elliptique

L'opérateur différentiel 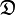$\mathfrak{D}$ est dit elliptique au point 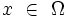$x \ \in \ \Omega$ si et seulement si :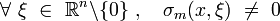
$\forall \ \xi \ \in \ \R^n \backslash \{ 0\} \ , \quad \sigma_m (x, \xi) \ \ne \ 0$
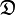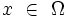$\mathfrak{D}$ est dit elliptique dans $Ω$ s'il est elliptique pour tout point $x \ \in \ \Omega$ .

Opérateur hyperbolique

L'opérateur différentiel 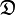$\mathfrak{D}$ est dit hyperbolique dans la direction $η$ au point 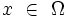$x \ \in \ \Omega$ si et seulement si : $\sigma_m (x, \eta) \ne 0$ et si, pout tout $ξ$ non colinéaire à $η$ , les racines $λ i$ de l'équation :
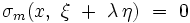
$\sigma_m (x, \ \xi \ + \ \lambda \, \eta) \ = \ 0$
sont toutes réelles. Si, de plus, les $m$ racines réelles sont toutes distinctes, l'opérateur 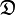$\mathfrak{D}$ est dit strictement hyperbolique dans la direction $η$ .

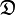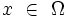$\mathfrak{D}$ est dit (strictement) hyperbolique dans la direction $η$ dans $Ω$ s'il est strictement hyperbolique dans la direction $η$ pour tout point $x \ \in \ \Omega$ .

Exemples importants pour la physique théorique

La physique théorique fait un usage abondant de trois opérateurs d'ordre 2 :

Opérateur laplacien

L'opérateur laplacien est un opérateur elliptique, qui s'écrit :

en coordonnées cartésiennes dans $\R^n$ : $\Delta \ = \ \sum_{k=1}^n \ \frac{\partial^2 ~~}{\partial x_k^2}$

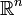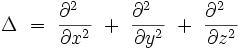
soit en coordonnées cartésiennes tridimensionnelles : $\Delta \ = \ \frac{\partial^2 ~~}{\partial x^2} \ + \ \frac{\partial^2 ~~}{\partial y^2} \ + \ \frac{\partial^2 ~~}{\partial z^2}$

Cet opérateur est notamment utilisé en mécanique newtonienne, en électromagnétisme, et en mécanique quantique non relativiste.

Opérateur d'alembertien

L'opérateur d'alembertien est un opérateur hyperbolique, qui s'écrit en coordonnées cartésiennes $(x, t)$ dans $\R^{n+1}$ :
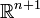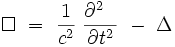
$\Box \ = \ \frac{1}{c^2} \ \frac{\partial^2 ~~}{\partial t^2} \ - \ \Delta$
où $Δ$ est le laplacien à $n$ variables d'espace, $t$ est le temps, et $c$ une constante positive, homogène à une vitesse. Cet opérateur est utilisé pour décrire la propagation des ondes à la vitesse $c$ dans l'espace-temps. Il est notamment utilisé en acoustique, en électromagnétisme, et en théorie quantique des champs.

Opérateur de la chaleur

L'opérateur de la chaleur, qui s'écrit en coordonnées cartésiennes $(x, t)$ dans $\R^{n+1}$ :
$\frac{\partial ~}{\partial t} \ - \ \tilde{D} \ \Delta$
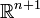où $Δ$ est le laplacien à $n$ variables d'espace, $t$ est le temps, et 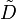$\tilde{D}$ est ici une constante, appelée coefficient de diffusion. Cet opérateur est dit parabolique.

Article connexe : équation de la chaleur.

Opérateur différentiel à coefficients constants

Si les coefficients $a α$ sont indépendants des $n$ variables d'espace $x k$ , le symbole de l'opérateur différentiel 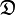$\mathfrak{D}$ d'ordre $m$ est seulement une fonction $σ(ξ)$ des $n$ variables $ξ$ polynomiale en $ξ$ :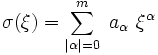
$\sigma (\xi) = \sum_{|\alpha| = 0}^m \ a_{\alpha} \ \xi^{\alpha}$
de telle sorte que :
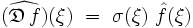
$(\widehat{\mathfrak{D} \, f})(\xi) \ = \ \sigma (\xi) \ \hat{f}(\xi)$
Le symbole principal de l'opérateur différentiel 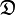$\mathfrak{D}$ d'ordre $m$ à coefficients constants est la fonction des $n$ variables $ξ$ :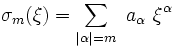
$\sigma_m (\xi) = \sum_{|\alpha| = m} \ a_{\alpha} \ \xi^{\alpha}$
Cas général

On a vu que plus haut :
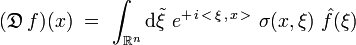
$(\mathfrak{D} \,f)(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \sigma (x,\xi) \ \hat{f}(\xi)$
Pour un opérateur différentiel dont les coefficients $a α (x)$ ne sont pas constants, le symbole $σ(x,ξ)$ dépend des coordonnées d'espace $x$ , et on a :
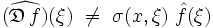
$(\widehat{\mathfrak{D} \, f})(\xi) \ \ne \ \sigma (x,\xi) \ \hat{f}(\xi)$
Expression de la transformée de Fourier

Partons de la relation générale :
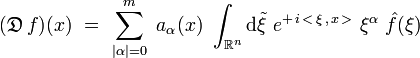
$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ a_{\alpha}(x) \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \xi^{\alpha} \ \hat{f}(\xi)$
Si l'on introduit la transformée de Fourier des coefficients :
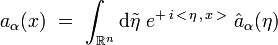
$a_{\alpha}(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\eta} \ e^{+ \, i \, < \, \eta \, , \, x \, >} \ \hat{a}_{\alpha}(\eta)$
on obtient :
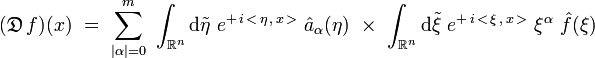
$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{\eta} \ e^{+ \, i \, < \, \eta \, , \, x \, >} \ \hat{a}_{\alpha}(\eta) \ \times \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \xi^{\alpha} \ \hat{f}(\xi)$
soit :
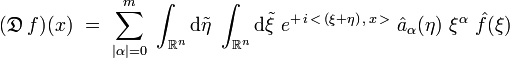
$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{\eta} \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, (\xi + \eta ) \, , \, x \, >} \ \hat{a}_{\alpha}(\eta) \ \xi^{\alpha} \ \hat{f}(\xi)$
A $ξ$ fixé, on fait le changement de variable : $\eta \to t = \xi + \eta$ , ce qui donne :
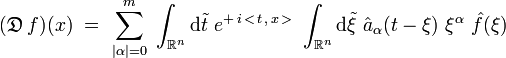
$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{t} \ e^{+ \, i \, < \, t \, , \, x \, >} \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ \hat{a}_{\alpha}(t - \xi) \ \xi^{\alpha} \ \hat{f}(\xi)$
On reconnait le produit de convolution :
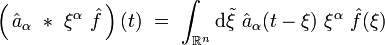
$\left( \, \hat{a}_{\alpha} \ * \ \xi^{\alpha} \ \hat{f} \, \right)(t) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ \hat{a}_{\alpha}(t - \xi) \ \xi^{\alpha} \ \hat{f}(\xi)$
d'où :
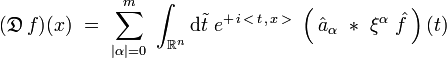
$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{t} \ e^{+ \, i \, < \, t \, , \, x \, >} \ \left( \, \hat{a}_{\alpha} \ * \ \xi^{\alpha} \ \hat{f} \, \right)(t)$
qu'on peut réécrire :
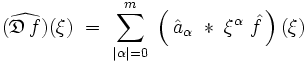
$(\widehat{\mathfrak{D} \, f})(\xi) \ = \ \sum_{|\alpha| = 0}^m \ \left( \, \hat{a}_{\alpha} \ * \ \xi^{\alpha} \ \hat{f} \, \right)(\xi )$
Voir aussi

Opérateur pseudo-différentiel

Dérivée partielle

Équation aux dérivées partielles

Bibliographie

Lars Hörmander ; The analysis of linear partial differential operators, Springer-Verlag (1983 à 1985). Traité de référence en quatre volumes, par le récipiendaire de la médaille Fields 1962. Le volume I est sous-titré : Distribution theory and Fourier analysis, et le volume II : Differential operators with constant coefficients. Les volumes III et IV sont consacrés à la théorie moderne via les opérateurs pseudo-différentiels.

Lars Hörmander ; Linear Partial Differential Operators, Springer-Verlag (1963). Le livre qui contient les travaux pour lesquels l'auteur a obtenu la médaille Fields en 1962.

Yu.V. Egorov & M.A. Shubin ; Foundations of the Classical Theory of Partial Differential Equations, Springer-Verlag (2^e édition - 1998), ISBN 3-540-63825-3. Premier volume d'une série qui en comporte neuf, écrits pour l' Encylopaedia of Mathematical Sciences. Les volumes suivants sont consacrés à la théorie moderne via les opérateurs pseudo-différentiels.

Michael E. Taylor ; Partial Differential Equations - Basic Theory, Series: Texts in Applied Mathematics, Vol. 23, Springer-Verlag (2^e édition - 1999), ISBN 0-387-94654-3. Premier volume d'une série qui en comporte trois. Les volumes suivants sont consacrés à la théorie moderne via les opérateurs pseudo-différentiels.

Portail des mathématiques

Portail de la physique

Ce document provient de « Op%C3%A9rateur diff%C3%A9rentiel ».

Catégories : Analyse à plusieurs variables | Théorie des opérateurs | Méthode mathématique de la physique

Contenu soumis à la licence CC-BY-SA. Source : Article Operateur differentiel de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Opérateur différentiel — Un opérateur différentiel est un opérateur agissant sur des fonctions différentiables. Lorsque la fonction est à une seule variable, l opérateur différentiel est construit à partir des dérivées ordinaires. Lorsque la fonction est à plusieurs… … Wikipédia en Français
opérateur différentiel — diferencialinis operatorius statusas T sritis fizika atitikmenys: angl. differential operator vok. Differentialoperator, m rus. дифференциальный оператор, m pranc. opérateur différentiel, m … Fizikos terminų žodynas
Operateur pseudo-differentiel — Opérateur pseudo différentiel En analyse mathématique, un opérateur pseudo différentiel est une extension du concept familier d opérateur différentiel, permettant notamment l inclusion d ordres de dérivation non entiers. Ces opérateurs pseudo… … Wikipédia en Français
Operateur laplacien — Opérateur laplacien Articles d analyse vectorielle Objet … Wikipédia en Français
Opérateur de Laplace — Opérateur laplacien Articles d analyse vectorielle Objet … Wikipédia en Français
Opérateur laplacien scalaire — Opérateur laplacien Articles d analyse vectorielle Objet … Wikipédia en Français
Operateur (mathematiques) — Opérateur (mathématiques) Pour les articles homonymes, voir opérateur. En mathématiques et en physique théorique, un opérateur est une application entre deux espaces vectoriels topologiques. Sommaire 1 Définition d un opérateur … Wikipédia en Français
Opérateur (mathématique) — Opérateur (mathématiques) Pour les articles homonymes, voir opérateur. En mathématiques et en physique théorique, un opérateur est une application entre deux espaces vectoriels topologiques. Sommaire 1 Définition d un opérateur … Wikipédia en Français
Opérateur mathématique — Opérateur (mathématiques) Pour les articles homonymes, voir opérateur. En mathématiques et en physique théorique, un opérateur est une application entre deux espaces vectoriels topologiques. Sommaire 1 Définition d un opérateur … Wikipédia en Français
Operateur integral — Opérateur intégral En mathématiques, un opérateur intégral (qu on nomme aussi transformée intégrale) est un opérateur qui se construit à partir d intégrales, et qui regroupe de nombreuses transformées courantes, comme la transformée de Fourier,… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts