Matrice des paiements

Matrice des paiements

Matrice des gains

La matrice des gains, matrice de paiement ou encore matrice des paiements (anglicismes issus de payoff matrix) est un moyen de représenter un jeu sous forme normale sous la forme d'un tableau indiquant les gains (ou paiements) associés à chaque action en fonction des actions de l'autre joueur.

Théoriquement, il est possible d'envisager des tableaux de n'importe quelle dimension, chaque dimension représentant un joueur. En pratique, seuls les tableaux en deux dimension sont aisément compréhensibles. Les matrices des paiements sont donc le plus souvent employés dans le cas de jeux à deux joueurs. Pour les mêmes raisons, elles ne sont employés que dans les jeux à un nombre raisonnable de stratégies.


Définition

Pour un jeu à deux joueurs et à un nombre fini de stratégies, la matrice des paiements est un tableau de couples de réels à m1 lignes et m2 colonnes :

\begin{bmatrix} a_{11} & a_{1 2} & \cdots & a_{1 m_2} \\ a_{12} & a_{2 2} & \cdots & a_{2 m_2} \\ \vdots & \vdots & \vdots & \vdots \\ \\ a_{m_1 1} & a_{m_1 2} & \cdots & a_{m_1 m_2} \end{bmatrix}

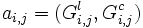où a_{i,j}=(G^l_{i,j},G^c_{i,j}) donne les gains Gc du joueur colonne et ceux Gl du joueur ligne si le joueur ligne choisit la stratégie i et le joueur colonne la stratégie j.

On peut remarquer que dans le cas général, les jeux n'ont pas à être symétriques (ce n'est le cas que si ai,j = aj,i), ni à présenter le même nombre de stratégies pour chaque joueur.

Dilemme du prisonnier

Considérons le jeu connu sous le nom de dilemme du prisonnier. Les deux joueurs sont deux criminels, entendus en même temps, séparément l'un de l'autre et sans possibilité de communiquer à propos d'un crime commis en commun. Chaque prisonnier peut soit nier le crime (C, pour coopérer), soit plaider coupable et servir de témoin à charge contre son complice (D, pour dévier). Le résultat de chaque stratégie en nombre d'années de prison est comme suit :

(C) (D)
(c) 1,1 20,0
(d) 0,20 10,10

Le premier prisonnier (Ligne) peut donc choisir de coopérer ou de dévier. De même, le prisonnier colonne choisir entre coopérer et dévier. Si les deux coopèrent, ils écopent d'un an de prison chacun. S'ils dévient tous les deux, ils écopent de dix ans chacun. Si Ligne coopère et que Colonne dévie, Colonne est libéré, et Ligne prend vingt ans de prison. Inversement, si Ligne dévie et Colonne coopère, Ligne est libre et Colonne en prend pour vingt ans.

Stratégies mixtes

Pour représenter un jeu en stratégies mixtes, on utilise la même formalisation que précédemment en ajoutant, pour chaque stratégie, la probabilité qu'elle soit jouée par un joueur. Ces probabilité se notent usuellement sur une ligne supplémentaire au-dessus des stratégies du joueur colonne, et sur une colonne supplémentaire insérée avant les stratégies du joueur ligne.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Matrice des gains ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice des paiements de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Matrice Des Gains — La matrice des gains, matrice de paiement ou encore matrice des paiements (anglicismes issus de payoff matrix) est un moyen de représenter un jeu sous forme normale sous la forme d un tableau indiquant les gains (ou paiements) associés à chaque… …   Wikipédia en Français

  • Matrice des gains — La matrice des gains, matrice de paiement ou encore matrice des paiements (anglicismes issus de payoff matrix) est un moyen de représenter un jeu sous forme normale sous la forme d un tableau indiquant les gains (ou paiements) associés à chaque… …   Wikipédia en Français

  • Théorie des jeux — La théorie des jeux est un ensemble d outils pour analyser les situations dans lesquelles ce qu il est optimal de faire pour un agent (personne physique, entreprise, animal, ...) dépend des anticipations qu il forme sur ce que un ou plusieurs… …   Wikipédia en Français

  • Theorie des jeux — Théorie des jeux Le dilemme du prisonnier est une célèbre illustration en théorie des jeux d un jeu à somme non nulle. La théorie des jeux constitue une approche mathématique de problèmes de stratégie tels qu’on en trouve en recherche… …   Wikipédia en Français

  • Théorie des jeux comme paradigme en science sociale — Théorie des jeux Le dilemme du prisonnier est une célèbre illustration en théorie des jeux d un jeu à somme non nulle. La théorie des jeux constitue une approche mathématique de problèmes de stratégie tels qu’on en trouve en recherche… …   Wikipédia en Français

  • Projet:Économie/Liste des articles — Le but de cette page est de lister les articles de Wikipédia relatifs à l économie. Ainsi, ceux et celles intéressés par le sujet peuvent suivre les changements en cliquant « Suivi des liens ». Sommaire 1 Articles 1.1 0 9 1.2 A 1.3 B …   Wikipédia en Français

  • Gestion des déchets radioactifs en France — La gestion des déchets radioactifs en France concerne deux aspects: celle du traitement du combustible usé, et celle du stockage des « déchets ultimes », non revalorisables (ce concept de « déchet ultime » n est pas spécifique …   Wikipédia en Français

  • Traitement des déchets radioactifs en France — Gestion des déchets radioactifs en France La loi française du 28 juin 2006 distingue les déchets radioactifs des matières radioactives valorisables : l uranium appauvri, le combustible irradié, l uranium dit de traitement (ou de… …   Wikipédia en Français

  • Liste des pièces de monnaie de la Confédération suisse — Article principal : Franc suisse. Pièces suisses actuellement en circulation Les pièces de monnaie de la Confédération suisse en circulation et ayant cours légal en Suisse depuis 1850, et au Liechtenstein dès 1924 …   Wikipédia en Français

  • Prix prédateurs et théorie des jeux — Prix prédateurs Les prix prédateurs sont une stratégie commerciale permettant à une entreprise déjà présente sur un marché de protéger ou d’étendre leurs parts de marché au détriment de concurrents potentiels ou existants. On parle ainsi de prix… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”