- Théorie des jeux comme paradigme en science sociale
-
Théorie des jeux
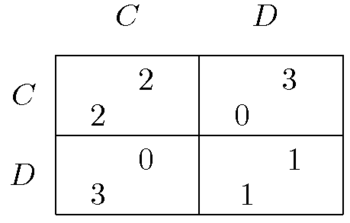 Le dilemme du prisonnier est une célèbre illustration en théorie des jeux d'un jeu à somme non nulle.
Le dilemme du prisonnier est une célèbre illustration en théorie des jeux d'un jeu à somme non nulle.
La théorie des jeux constitue une approche mathématique de problèmes de stratégie tels qu’on en trouve en recherche opérationnelle et en économie. Elle étudie les situations où les choix de deux protagonistes - ou davantage - ont des conséquences pour l’un comme pour l’autre. Le jeu peut être à somme nulle (ce qui est gagné par l’un est perdu par l’autre, et réciproquement) ou, plus souvent, à somme non-nulle. Un exemple de jeu à somme nulle est celui de la mourre, ou celui du pierre-feuille-ciseaux.
Sommaire
Historique
Trois grandes étapes
- La théorie des jeux initiale, de John von Neumann et Oskar Morgenstern, utilisait des cas de choix qui restaient les mêmes au cours du temps, et qui étaient à somme nulle.
- Les jeux à somme non-nulle furent étudiés ensuite, et utilisés dans la théorie de la négociation. On découvrit que leur étude permettait d’aborder de façon mathématique des questions jusque là restées d’ordre philosophique, comme la morale.
- On s’intéressa ensuite aux jeux où le choix se posait en termes différents à chaque étape, que l’on nomma un temps théorie des jeux combinatoires. Celle-ci est plutôt aujourd’hui, pour des raisons de commodité et de communauté de concepts, considérée comme une branche soit de la théorie des graphes, soit de ce qu’on nomme l’intelligence artificielle.
Détails
Bien qu’ayant fait l’objet de résultats assez anciens, à partir des travaux de Blaise Pascal sur la question des parties qui a donné une première intuition des probabilités et de l’espérance mathématique, et de son étonnant pari, la théorie des jeux n’est devenue une branche importante des mathématiques qu’à partir des années 1940, particulièrement après la publication en 1944 de la Théorie des jeux et du comportement économique (Theory of Games and Economic Behavior) par John von Neumann et Oskar Morgenstern. Cet ouvrage fondateur détaillait la méthode vue plus haut de résolution des jeux à somme nulle.
La théorie rencontra lors de sa présentation une vive opposition de la part des états-majors : si ceux-ci acceptaient volontiers l’usage de tirages au hasard dans les jeux de Kriegspiel des écoles militaires, l’idée de remettre au sort, au nom des stratégies mixtes le fait d’escorter réellement ou non tel ou tel convoi n’enthousiasmait guère ceux qui, issus du terrain et sachant ce qu’étaient des pertes humaines, jugeaient le procédé pour le moins cavalier.
Vers 1950, John Nash a présenté une définition d’une stratégie optimale pour un jeu à plusieurs joueurs, dite équilibre de Nash. Ce résultat tardif[1] génial a été raffiné par Reinhard Selten ; cela leur a valu le « prix Nobel d'économie » en 1994 pour leurs travaux sur la théorie des jeux, avec John Harsanyi qui avait travaillé sur les jeux en information incomplète.
L’association entre jeu et nombre par Conway a été établie dans les années 1970.
Grandes lignes
La théorie des jeux étudie les comportements - prévus, réels, ou tels que justifiés a posteriori - d’individus face à des situations d’antagonisme, et cherche à mettre en évidence des stratégies optimales. Des situations apparemment très différentes peuvent parfois être représentées avec des structures d’incitation comparables, et constituant autant d’exemples d’un même jeu.
La théorie des jeux non coopératifs s’applique à des situations où des joueurs jouent sciemment alors qu’ils ont des buts au moins partiellement antagonistes (elle ne s’applique donc pas aux situations de pleine coopération, mais à la compétition ou à sa variante plus fréquente que l’on nomme la coopétition). Elle ne concerne pas les situations de jeu contre une nature dépourvue de buts, ne dressant pas de plans, situations où il y aurait donc en fait qu’un seul joueur.
Types de jeux
La théorie des jeux classifie les jeux en catégories en fonction de leurs approches de résolution. Les catégories les plus ordinaires sont :
Jeux coopératifs et compétitions
Les jeux coopératifs sont les jeux dans lesquels on cherche la meilleure situation pour les joueurs sur des critères tels que la justice. On considère qu'ensuite les joueurs vont jouer ce qui aura été choisi, il s'agit d'une approche normative. Par exemple, à un croisement, chacun des deux automobilistes a la possibilité de passer ou non. Le code de la route impose sa stratégie à chacun des joueurs par une signalisation.
Dans les jeux coopératifs, on étudie la formation de coalitions entre les joueurs afin d’obtenir un meilleur résultat pour ses membres. C’est un concept qui n’existe pas dans les jeux non coopératifs. Le jeu non coopératif à n joueurs est une simple généralisation du jeu à deux joueurs. Par contre, dans un jeu coopératif à deux personnes il n’y a qu’une seule coalition tandis qu’avec 4 joueurs on a déjà 15 coalitions possibles.
Un autre concept utilisé dans les jeux coopératifs est la fonction caractéristique. Soit v(C) la fonction qui donne la valeur maximin de la coalition C. Cette expression est appelée la fonction caractéristique du jeu. Par exemple, si la coalition comprenant les joueurs 1 et 2 obtient un profit de 600, on écrit v(1,2) = 600.
On peut décrire un jeu en indiquant les valeurs de la fonction caractéristique pour toutes les coalitions possibles, y compris celles ne comprenant qu'un seul joueur. On parle souvent du jeu v au lieu de dire un jeu ayant la fonction caractéristique v.
Dans un jeu à n personnes, il y a 2n − 1 coalitions non vides et autant de valeurs de la fonction caractéristique. Par définition, la valeur de la fonction caractéristique d'une coalition vide est égale à zéro.
Si des coalitions disjointes (C et Z) sont réunies en une grande coalition, on peut admettre que la valeur de la fonction caractéristique de cette grande coalition soit au moins égale à la somme des valeurs des deux coalitions:
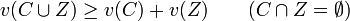
(propriété de superadditivité)
Soit N={1,2,…,n} l’ensemble des joueurs et xi la somme ou l’utilité que le joueur i reçoit. Une imputation est un vecteur
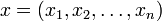 qui indique ce que chaque joueur obtient dans le jeu. Prenons maintenant deux imputations possibles x et y de la coalition S. On dit que y est dominée par x si :
qui indique ce que chaque joueur obtient dans le jeu. Prenons maintenant deux imputations possibles x et y de la coalition S. On dit que y est dominée par x si :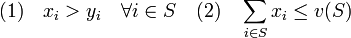
L’ensemble des imputations qui ne sont pas dominées est appelé le noyau ou le coeur d’un jeu coopératif. L’imputation du noyau ne peut pas être bloquée par aucune autre imputation.
Par exemple, le jeu avec les fonctions caractéristiques suivantes:
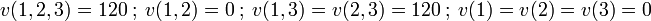
a un noyau correspondant au point (0,0,120). Il suffit de modifier une fonction caractéristique (par exemple, v(1,2)=120) pour obtenir un noyau vide.
Plusieurs autres solutions d’un jeu coopératif ont été proposées, entre autres la valeur de Shapley qui est une imputation unique.
Article détaillé : Jeu coopératif.Théorie de la négociation
La théorie moderne de la négociation est articulée sur le fait qu’une négociation constitue un jeu à somme non-nulle. L’art de la négociation consiste donc moins à faire céder l’interlocuteur sur la ligne principale d’opposition (un prix, par exemple) qu’à trouver des arrangements extérieurs à cette ligne qui apporteront beaucoup à l’un sans coûter trop cher à l’autre (stratégies dites Gagnant-gagnant).
Depuis longtemps, tout cela était utilisé dans les négociations :
- « Je ne peux accepter ce coût FOB, mais puis le considérer en CIF. »
- « Si je vous en prends deux, m’accordez-vous 5% de remise ? »
- « Je vous en offre tant, mais il faut vous décider tout de suite. »
voire entre particuliers :
- « Je veux bien te le laisser à ce prix-là, mais tu offres le café ! »
« Coopétition »
La coopétition est le partage d'information au sein d'un réseau socio-professionnel de concurrence. On parle aussi de compétition transparente. La coopétition peut s'appliquer tant à des services de recherche et développement des organisations (qui se livrent par ailleurs une guerre féroce en matière commerciale), qu'au monde du développement des logiciels libres, qui fait appel au principes de fourches (un projet se scinde en deux en cas de passage de la coopération à la compétition), tout en laissant les deux codes logiciels produits en concurrence accessibles pour les deux groupes de développeurs. Par extension, la coopétition s'applique dans tout contexte de gestion de la complexité socio-professionnelle, car le principe de base est que l'information prend de la valeur lorsqu'elle est partagée, et que justement, c'est en étant émetteur d'information stratégiques qu'on prend une position dominante dans un groupe de compétiteurs, face à divers clients potentiels.
Jeux de stratégie à somme nulle et non nulle
- Les jeux à somme nulle sont tous les jeux où la somme « algébrique » des gains des joueurs est nulle. Ce que gagne l’un est nécessairement perdu par un autre, l'enjeu est la répartition du total fixé, qu'on peut supposer réparti à l'avance, ce qui ramène au cas où les gains sont vraiment nuls (d'où la dénomination). Les échecs ou le poker sont des jeux à somme nulle car les gains de l’un sont très exactement les pertes de l’autre.
- Les situations d’affaires, la vie politique ou le dilemme du prisonnier sont des jeux à somme non-nulle car certaines issues sont globalement plus profitables pour tous, ou plus dommageables pour tous. On a commencé historiquement par étudier les jeux à somme nulle, plus simples. Au-delà de la matière-énergie avec la loi de la conservation de la somme algébrique nulle, le jeu à somme non-nulle est concevable, dans lequel le gain de l'un peut profiter à l'autre. Tel est le cas avec l'information, la communication et l'apprentissage où l'information est une des trois composantes fondamentales avec la matière et l'énergie. L'exemple illustratif le plus simple est l'information génétique de l'ADN transcrite sur l'ARN pour être « lue », « traduite » et organiser la matière et l'énergie biologiques. En sciences sociales, on cite parfois l'idéologie d'harmonie industrielle du Japon moderne (coalition tripartite capital-travail-gouvernement) comme exemple de jeu à somme non nulle. Dans le commerce international, l'exemple de ce jeu à somme non nulle est la concurrence coopérative des Tigres asiatiques et Dragons asiatiques où le gain de l'un profite aux autres, dans la foulée du miracle économique japonais des années 1950-1960 qui a ouvert les portes à la Corée, à Hong Kong, à Singapour, à Taïwan et au Viêt Nam, dans une coévolution technico-commerciale.[réf. nécessaire]
- En écologie, la coévolution est un autre exemple, dans la nature, de la somme non nulle où le changement de l'un facilite et fait la promotion du changement de l'autre.
On pourrait croire qu'il suffirait pour ramener un jeu à somme non-nulle à un jeu à somme nulle d'y ajouter un joueur simplet, le « tableau », sorte de non-player character qui compenserait les pertes nettes des joueurs. Ce n’est pas le cas : un joueur est censé défendre rationnellement ses intérêts dans la mesure de ses possibilités; cet ajout formel, introduisant une dissymétrie entre les « vrais » joueurs et le « tableau », complique l'analyse et celle-ci y perd plus qu’elle n’y gagne.
Jeu synchrone ou asynchrone
Dans un jeu synchrone, les joueurs décident de leur coup simultanément, sans savoir ce que les autres jouent. Dans un jeu asynchrone (ou alternatif, à deux joueurs), ils jouent les uns après les autres, en disposant à chaque fois de l’information sur le coup de l’adversaire. Une analyse des stratégies gagnantes est proposée pour le hex, un jeu de cette nature.
Jeux répétés
La répétition d’un jeu, avec connaissance des résultats intermédiaires, change souvent fondamentalement son déroulement (les meilleurs coups et la conclusion).
Par exemple, il peut être utile de prendre ponctuellement le risque de perdre « pour voir », tester les autres joueurs, et mettre en place des stratégies de communication par les coups joués (à défaut d’autre moyen de communication).
Il se développe également des phénomènes de réputation qui vont influencer les choix stratégiques des autres joueurs. Dans le dilemme du prisonnier, le fait de savoir qu’on va jouer plusieurs fois avec un dur qui n’avoue jamais mais se venge cruellement, ou avec un lâche qui avoue toujours, change radicalement la stratégie optimale.
Enfin, curieusement, le fait que le nombre total de parties soit connu à l’avance ou non peut avoir des effet importants sur le résultat, l’ignorance du nombre de coups rapprochant du jeu avec un nombre infini de coup, alors que sa connaissance rapproche au contraire du jeu à un seul coup (et ce, aussi grand que soit le nombre de coups !)
Information complète, information parfaite
On dit qu'un jeu est à information complète si chaque joueur connaît lors de la prise de décision :
- ses possibilités d'action
- les possibilités d'action des autres joueurs
- les gains résultants de ces actions
- les motivations des autres joueurs
Par ailleurs on parle de jeu à information parfaite dans le cas de jeu à mécanisme séquentiel, où chaque joueur a connaissance en détail de toutes les actions effectuées avant son choix.
Les échecs sont à information complète et parfaite. Du fait de l'incertitude sur les gains (cartes de l'adversaire cachées), le poker est à information incomplète. La phase d'enchères vérifie les propriétés d'information parfaite, mais en assimilant le tirage des cartes à l'action d'un joueur fictif (souvent appelé Nature), la théorie des jeux exclut en général le poker des jeux à information parfaite.
Les situations réelles sont rarement en information complète, et ce cas ne sert souvent qu’aux approximations confiantes.
Les jeux en information incomplète sont des situations stratégiques où l'une des conditions n'est pas vérifiée. Ce peut être par l'intervention du hasard au cours du jeu (cas fréquent dans les jeux de société), ou parce qu'une des motivations d'un acteur est cachée (domaine important pour l'application de la théorie des jeux à l'économie).
Les jeux en information à la fois imparfaite et incomplète sont de loin les plus complexes. Dans ces jeux certains joueurs peuvent disposer d'informations propres sur la manière dont le hasard va intervenir dans l'issue du jeu (une meilleure connaissance des probabilités d'occurrence de tel ou tel événement qui va affecter le cours du jeu, par exemple). Les jeux de guerre (war games) relèvent typiquement de cette catégorie, l'aléa sur la réussite d'un engagement entre corps de troupes dépendant d'informations non partagées par les adversaires sur les rapports de force entre ces troupes.
Pour être complet, il convient aussi de distinguer les jeux à mémoire parfaite et à mémoire imparfaite. Les jeux à mémoire « parfaite » sont des situations où chaque joueur peut se rappeler à tout moment de la suite de coups qui ont été joués précédemment, au besoin en notant au fur et à mesure les coups joués. Les jeux à mémoire « imparfaite » supposent une sorte d'amnésie de la part des joueurs. Les jeux de guerre sont des exemples de jeux à mémoire imparfaite si les commandements de zones opérationnelles ne parviennent pas à communiquer entre eux ou avec l'État-Major et donc n'ont pas trace des mouvements déjà effectués par les troupes amies lorsqu'elles doivent décider de leurs propres mouvements. Un jeu typique est le 21 ou blackjack : la convention selon laquelle la suite de paquets de cartes n’est pas battue entre deux jeux peut donner un léger avantage au joueur dès lors que celui-ci prend en compte cette information partielle.
Jeux déterminés
Les jeux de Nim forment un cas particulier de jeu à somme nulle, sans intervention du hasard et dans la plupart des cas à nombre de situations finies. Dans leur cas particulier, la théorie des graphes fournit un outil plus utile que la théorie des jeux à proprement parler. La notion de noyau du jeu (ensemble des nœuds depuis lesquels la victoire est assurée si l’on y parvient en cours de jeu et qu’on joue de façon optimale ensuite) y est caractérisée.
Représentations des jeux
Forme extensive
Dans tous les jeux, les décisions peuvent être représentées par un arbre, dont chaque nœud est associé au joueur qui décide. Chaque option constitue une branche. Les gains de tous sont associés aux terminaisons ou feuilles de l'arbre. Un joueur n’a toutefois pas besoin de savoir comment il est parvenu à un nœud : seul compte l'état présent du jeu, et les positions recherchées dans le futur. Lorsque certains mouvements ne sont autorisés qu’après un événement donné, cet événement n’est qu’un des éléments à matérialiser dans l’état présent du jeu et n'a pas besoin de faire partie d'un historique.
Une forme extensive de jeu est un arbre de décision décrivant les actions possibles des joueurs à chaque étape du jeu, la séquence de tours de jeu des joueurs, ainsi que l'information dont ils disposent à chaque étape pour prendre leur décision. Cette information est représentée sous forme d'ensembles d'information qui forment une partition des nœuds de l'arbre, chaque classe de la partition contenant les nœuds non distinguables par le joueur à une étape du jeu. Si ces classes sont des singletons, c’est-à-dire que chacune est constituée d'un seul nœud de l'arbre du jeu, le jeu est dit à information parfaite, ce qui signifie que chaque joueur sait à tout moment où il se situe dans l'arbre du jeu. Dans le cas contraire, le jeu est dit à information imparfaite[2]. L'information imparfaite est représentée sous la forme d'un joueur non rationnel : la « Nature », joueur qui prend aléatoirement certaines décisions à telle ou telle étape du jeu, orientant la suite du jeu vers un certain sous-arbre de l'arbre du jeu.
Forme normale
Définition
Article principal : Jeu sous forme normale
Un jeu sous forme normale est la donnée de l'ensemble des joueurs, de l'ensemble des stratégies pour chaque joueur et des paiements associés à toute combinaison possible de stratégies.
Représentation tabulaire
Si le jeu ne comporte que deux joueurs et un nombre raisonnablement restreint de stratégies possibles, on peut représenter le jeu sous la forme d'un tableau nommé matrice des gains.
Il s'agit d'un tableau à double-entrée qui énumère sur chaque côté les stratégies possibles des joueurs respectifs. Dans la case à la croisée de deux stratégies, on note le couple de gains des deux joueurs. C’est ce qu’on nomme (par convention) la matrice des paiements.
Si le jeu est à somme nulle et à deux joueurs, alors on peut ne noter que les gains du premier joueur : ceux du second sont directement opposés. Le tableau de gains se ramène alors à une matrice.
On peut, avec un nombre réduit de stratégies, tenter de représenter avec une matrice un jeu à trois ou quatre joueurs, mais cela pose souvent plus de problèmes d’interprétation et de lecture que ça n’apporte de réponses.
Résolution d’un jeu à somme nulle
1\2 (A) (B) (C) (a) 30 -10 20 (b) 10 20 -20 Les deux joueurs décident simultanément de leur stratégie.
Raisonnements intuitifs
Le joueur (1) a le choix entre (a) et (b). Il peut se dire : « La stratégie (b) peut me faire perdre 20, et au plus gagner 20. En revanche, avec la stratégie (a) je peux gagner jusqu’à 30, et au pire perdre 10. » Ce type de réflexion correspond aux stratégies « Maxi-Max » (maximiser le gain possible sans considération pour les pertes possibles) et « Maxi-Min » (maximiser le pire résultat possible), qui en l’occurrence donne le même choix : l’option a.
De même, le joueur (2), touchant l’opposé des valeurs du tableau, qui réfléchirait de même verrait que Maxi-Min élimine (A) à cause de la perte maximum de 30, mais ne permet pas de trancher entre (B) et (C), où la perte maximum est de 20. Et que Maxi-Max classe les trois options par ordre croissant : A (meilleur résultat possible : -10) B (+10), C (+20). Cela le pousserait à choisir (C).
Le résultat serait alors a-C : le joueur (2) perd 20 au profit de (1).
Mais le joueur (2) peut aussi essayer d’anticiper le choix de (1). Il voit ainsi que si (1) joue le maximin, lui-même a intérêt à choisir (B), ce qui lui permet de gagner 10.
Et si à son tour le joueur 1 anticipe cette déviation et préfère faire (b) pour alors toucher 20 ? Alors (2) devrait à nouveau choisir (C) : nous voilà revenu au point de départ !
La notion de stratégie et d’équilibre mixte
Aucune réponse ne s’impose. Comment s’en sortir ?
Une première réponse possible est de jouer au hasard, avec une probabilité égale pour tous les coups possibles, sans se préoccuper des gains. Cela n’apparaît pas optimum, il y a certainement mieux à faire.
Une seconde stratégie est de tenter d’attribuer a priori une probabilité aux actions de l’adversaire, et d’opter pour la meilleure réponse adaptée. Ainsi, si (2) attribue une probabilité 50/50 aux options de (1), il doit jouer aussi à 50/50 (B) et (C). Mais l’adversaire n’est pas un dé qui se comporte au hasard : lui aussi va anticiper. Si c’est (1) qui réfléchit, il voit bien qu’il est absurde de supposer que (2) va jouer (A) dans un tiers des cas. Là encore il y a certainement mieux à faire.
Introduction de probabilités
John von Neumann est parvenu à sortir de cet imbroglio à l’aide des probabilités. Au lieu de décider fermement d’une action, chaque joueur va agir de façon probabiliste, chaque coup étant choisi par hasard avec un processus aléatoire (par exemple un jeu de dès, ou une table de valeurs aléatoires). Il est clair que l’adversaire ne peut pas deviner notre comportement si nous ne le connaissons pas d’avance nous-mêmes !
La solution que von Neumann fournit au problème constitue le théorème du minimax.
Point-selle
Il est remarquable que ce choix stratégique reste le meilleur même si l’adversaire en a connaissance.
On est ainsi amené à introduire le concept intéressant, dans les stratégies mixtes, de point-selle : il s’agit du choix de probabilité optimal pour les deux joueurs : celui qui s’en écarte se pénalise du même coup (même si cette stratégie lui est défavorable, car les autres le seront encore plus). Le thème avait été entrevu par Auguste Detoeuf : Si vous n’avez qu’un risque sur mille d’être convaincu de mensonge, ne mentez pas plus d’une fois sur mille, car cette fois-là annulera à elle seule toutes les autres où vous avez dit la vérité. Detoeuf, industriel responsable, évite sciemment de préciser qu’il y aura parfois même avantage à mentir effectivement une fois sur mille plutôt que dire toujours la vérité.
Les stratégies mixtes sont empiriquement bien connues des diplomates et des joueurs de poker, qui savent les bénéfices potentiels obtenus en cachant leurs plans, même quand il y en a un qui semble évident. Cette idée frappera Philip K. Dick qui lui consacrera son roman Loterie solaire.
Applications
Les champs d’application de la Théorie des Jeux sont très variés par exemples :
- Défense : modélisation de la dissuasion nucléaire,
- Biologie évolutive , sociologie et génétique : des chercheurs ont utilisé la stratégie des jeux pour mieux comprendre l’évolution du comportement des espèces face à la modification de leur environnement. Plus précisément, la théorie des jeux est parfois utilisée pour identifier les stratégies pour lesquelles le gain (mesuré en survie et/ou reproduction) est le plus élevé.[3],
- Organisation : développement de système multi-agents,
- Marketing et stratégie d’entreprise
- Domaine de l'économie, celles où existent un nombre réduit de compétiteurs (oligopole)
Article détaillé : Théorie des jeux comme paradigme en science sociale.Elle cherche les stratégies rationnelles dans des situations où les gains d’un acteur dépendent non seulement de son comportement et des conditions de marché, mais aussi de celui des autres intervenants, lesquels peuvent poursuivre des objectifs différents ou contradictoires. On lui trouve aussi des applications en sciences politiques.
Les résultats peuvent être appliqués à des divertissements (comme le jeu télévisé « Friend or Foe » sur une chaîne câblée spécialisée aux États-Unis, Game Show Network) ou à des considérations plus poignantes :
- la crise des missiles de Cuba ;
- les politiques de constitution de convois de bateaux en temps de guerre ;
- la façon de gérer un coup de surprise politique (Nasser à Suez, de Gaulle au Québec, Ieltsine lors du putsch, annonces électorales...) ou marketing ;
- la lutte contre le terrorisme.
Le Professeur Thomas Schelling, « prix Nobel d'économie » 2005, s'est spécialisé dans l'explication des diverses stratégies utilisées (à utiliser) dans les conflits internationaux, tels la guerre froide et la guerre nucléaire (dissuasion..)
Albert W. Tucker a par exemple diffusé de nombreuses interprétations du dilemme du prisonnier dans la vie courante. Des biologistes ont utilisé la théorie des jeux pour comprendre et prévoir les résultats de l’évolution, en particulier la notion d’équilibre évolutivement stable introduit par John Maynard Smith dans son essais La théorie des jeux et l’évolution de la lutte (Game Theory and the Evolution of Fighting). Voir aussi son livre Evolution and the Theory of Games.
Il est à remarquer qu’en théorie de l’évolution, l’adversaire principal d’un individu n’est pas vraiment l’ensemble de ses prédateurs, mais l'ensemble des autres individus de son espèce et des autres espèces apparentées. Comme le fait remarquer Richard Dawkins, un brontosaure n'a pas besoin, pour survivre, de courir plus vite que le tyrannosaure qui le poursuit (ce qui lui serait impossible), mais simplement plus vite que le plus lent de ses congénères. Des phénomènes semblables se produisent en économie. Tout cela rejoint des considérations psychologiques : la conflictualité est plus liée à la ressemblance qu'à la différence.
Les probabilités fournissent à la théorie des jeux un outil conceptuel. Les statistiques peuvent l’alimenter en données, et les techniques d’optimisation lui fournir des résultats de calcul.
Gains et aversion au risque
Dans l’exemple en stratégie mixte défini plus haut, les participants au jeu ont été considérés comme neutres au risque. Cela signifie qu’ils considèrent qu’avoir une chance sur deux d’obtenir 20 et une chance sur deux de ne rien avoir est équivalent à obtenir 10.
Cependant, la plupart des personnes sont averses au risque, et préfèrent les issues les plus sûres -- et n’accepteraient un risque supplémentaire que contre une espérance de gain plus important.
Un exemple de cette aversion au risque peut être remarqué au cours de jeux télévisés. Si, par exemple, on propose aux candidats soit une chance sur trois d’avoir 50 000 € soit 10 000 € à coup sûr, beaucoup préféreront la garantie de changer leur ordinaire. Le revenu supplémentaire espéré qui est exigé pour compenser l’aversion au risque est appelé, en finance, la prime de risque. La souscription de polices d’assurance (là où ce n’est pas obligatoire) se justifie également par aversion au risque.
Il est donc rationnel de construire une mesure de l’utilité subjective
- qui soit une fonction du gain et du risque,
- qui satisfasse toujours le critère de neutralité au risque,
- et qui corresponde donc à un tableau de gains en stratégie mixte.
Plus généralement, l’utilité tient compte du fait que les grosses variations sont plus significatives que les petites (on achète volontiers un billet de loterie ou de Loto, dont le prix très faible correspond à une perte négligeable, tandis que le gain serait significatif), et que la signification d’une variation décroît (il y a plus de différence d’utilité entre un gain de 1 000 et un gain de 1 001 000, qu’entre un gain de 1 001 000 et un gain de 2 001 000, même si la différence est de 1 million à chaque fois ; une chance sur cent de gagner un million est généralement préférée à une chance sur mille de gagner 10 millions, malgré l’espérance égale).
Inversement, il peut exister un désir d’acheter du risque ou de la peur : qu’il s’agisse d’un billet de loterie ou d’un film d’épouvante, l’excitation correspondant à une valeur en elle-même.
Bref, le fait d’acheter un billet de loterie ou de Loto, ou de jouer dans un casino, est motivé par deux composantes :
- la sécrétion d’adrénaline (comme lorsqu’on va voir un film d’action ou qu’on pratique un sport à risque)
- la différence qualitative entre :
- une perte probable qui passera inaperçue,
- un gain certes peu probable, mais qui procurera s’il se produit un changement qualititatif. Ce point a été défendu devant l’Académie des sciences par Émile Borel (en réaction contre une tendance de son époque à ne considérer que l’espérance mathématique comme fonction d’utilité) et est en général admis depuis lors compte-tenu de sa meilleure explication des comportements liés au jeu et à la souscription de polices d’assurance.
Jeux de chiffres
John Conway a mis en place une notation pour certains jeux et défini des opérations sur ces jeux, dans l’espoir d’étudier le jeu de go. À partir d’associations surprenantes d’idées, il a isolé une sous-classe avec des propriétés numériques, et a abouti à définir la classe très générale des nombres surréels. Cela dit, en dépit de ces progrès annoncés, aucun programme informatique n’arrive à jouer actuellement (2006) au go avec des performances de joueur international.
Notes
- ↑ Antoine-Augustin Cournot avait présenté des équilibres dans les jeux à deux joueurs (duopoles) mais ce résultat était inconnu de Nash.
- ↑ En fait le graphe du jeux peut-être vu comme n'étant plus un arbre, mais comme étant un Graphe acyclique orienté.
- ↑ Gouyon, P-H., Henry, J-P., Arnould, J. Les avatars du gène. Belin (Ed.)335p. ISBN 2-7011-2187-6
Bibliographie
- Ivar Ekeland, La théorie des jeux et ses applications à l'économie mathématique, Presses universitaires de France, Collection SUP. Le mathématicien 12, Paris, 1974.
- Oskar Morgenstern, John von Neumann : The Theory of Games and Economic Behavior, 3rd ed., Princeton University Press 1953
- Binmore, K. et Brandenburger, A. (1990), “Common knowledge and game theory,” in K. Binmore, Essays on the Foundations of Game Theory. Oxford: Blackwell.
- John Maynard Smith : Evolution and the Theory of Games, Cambridge University Press 1982
- Guillermo Owen, Game Theory, W.B. Saunders Company, Philadelphia, 1968
Voir aussi
Articles connexes
- Jeu mathématique
- Intelligence artificielle
- Paradoxe de Newcomb
- Classification des jeux
- Théorie combinatoire des jeux
- Théorie des mécanismes d'incitation
- Raisonnement rétrograde
- Théorie des jeux en relations internationales
- Théorie des enchères
Liens et documents externes
- (fr)Frédéric KOESSLER, Théorie des jeux / Game Theory
- (fr)Jacques-François Thisse, Théorie des jeux: une introduction
- (fr) Isabelle Olivieri & Pierre-Henri Gouyon, Génétique évolutive et théorie des jeux
- (fr)Michel Bruley, Système d'information décisionnel & Théorie des jeux
- (en)Paul Walker, An Outline of the History of Game Theory.
- (en)Alvin Roth: Game Theory and Experimental Economics page, http://www.economics.harvard.edu/~aroth/alroth.html Comprehensive list of links to game theory information on the Web
- (en)Mike Shor :Game Theory .net Note de cours, illustration interactives.
- (en)Don Ross: Review Of Game Theory.
- (en) Logiciels Gambit pour la théorie de jeux
- Portail de l’économie
- Portail des mathématiques
- Portail de la sociologie
Catégories : Théorie des jeux | Recherche opérationnelle | Management | Négociation | Sociologie d'intervention
Wikimedia Foundation. 2010.
