- Groupe alterné
-
En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous-groupe distingué du groupe symétrique des permutations d'un ensemble fini à n éléments. Ce sous-groupe est composé des éléments produits d'un nombre pair de transpositions. Une transposition est une permutation φ réduite à l'identité sauf sur exactement 2 éléments a et b. Cette propriété implique que φ(a) = b et φ(b) = a.
Il existe un groupe alterné pour chaque entier n supérieur ou égal à 2 ; il se note habituellement An (ou parfois
 en écriture Fraktur) et possède n ! / 2 éléments. Le plus petit groupe alterné, A2, est trivial, A3 est cyclique d'ordre 3, le suivant A4 est résoluble et, plus précisément, est produit semi-direct d'un groupe de Klein par un groupe cyclique d'ordre 3. À partir du groupe A5, les groupes alternés sont simples et non abéliens, donc non résolubles. Cette non résolubilité à partir de n = 5 possède comme conséquence le théorème d'Abel, stipulant qu'il ne peut exister d'expression générique par radicaux d'une équation algébrique de degré supérieur ou égal à 5.
en écriture Fraktur) et possède n ! / 2 éléments. Le plus petit groupe alterné, A2, est trivial, A3 est cyclique d'ordre 3, le suivant A4 est résoluble et, plus précisément, est produit semi-direct d'un groupe de Klein par un groupe cyclique d'ordre 3. À partir du groupe A5, les groupes alternés sont simples et non abéliens, donc non résolubles. Cette non résolubilité à partir de n = 5 possède comme conséquence le théorème d'Abel, stipulant qu'il ne peut exister d'expression générique par radicaux d'une équation algébrique de degré supérieur ou égal à 5.Le groupe alterné est la structure source de certains casse-tête mathématique comme le jeu de taquin ou le cube de Rubik. Les mouvements possibles dans les deux jeux cités sont des éléments d'un groupe alterné. Cette propriété permet de montrer qu'il n'est pas possible de permuter deux cases du taquin sans modifier le reste du jeu.
Les groupes alternés de degré 4 et 5 se représentent comme le groupe des rotations laissant invariant un polyèdre régulier, le tétraèdre pour A4 et le dodécaèdre régulier ou encore l'icosaèdre pour A5.
Sommaire
Construction du groupe
Définition
Un résultat, à la base de la définition de la signature, stipule que le nombre de transpositions nécessaire pour décomposer une permutation donnée est toujours de même parité. Ainsi, le cycle (abc), qui transforme a en b, b en c et c en a peut se décomposer en deux transpositions (bc), puis (ab) ou encore en (ac) puis (bc) mais jamais en un produit d'un nombre impair de transpositions.
Définition — Une permutation est dite paire lorsqu'elle se décompose en un nombre pair de transpositions. Dans le cas inverse, la permutation est dite impaire.
Cette définition est à l'origine de celle d'un groupe alterné.
Définition — Le groupe alterné de degré n, noté An, est le sous-groupe des permutations paires de degré n[1].
Remarque : On trouve aussi l'expression groupe alterné d'indice n, à la place de groupe alterné de degré n[2]. Ce choix est un peu ambigu, l'indice de An dans Sn désigne, pour d'autres auteurs, l'ordre du groupe quotient Sn/An[3]. On trouve encore le terme d'ordre pour décrire le degré[4]. Cette convention est plus rarement utilisée, car le terme d'ordre est utilisé en théorie des groupes pour décrire le cardinal d'un groupe, ce choix introduit une confusion parfois regrettable.
Propriétés élémentaires
Article détaillé : groupe symétrique.Dans toute la suite de l'article, n désigne un entier supérieur ou égal à 2. La définition précédente repose sur une propriété fondamentale partagée par toutes les permutations :
Propriété 1 — La parité du nombre de transpositions nécessaire pour décomposer une permutation donnée est indépendante de la décomposition choisie.
Cette propriété se démontre à l'aide du concept de signature d'une permutation, traitée dans le paragraphe suivant. Une fois établie, une deuxième propriété se démontre simplement :
Propriété 2 — L'ensemble An des permutations paires de Sn forme un sous-groupe distingué.
En effet, An est non vide car il contient l'élément neutre, qui se décompose en zéro transposition, ou encore en deux fois la même transposition. Si φ1 et φ2 sont deux permutations paires alors leur produit est aussi une permutation paire. Pour s'en rendre compte, il suffit de remarquer que φ1 et φ2 correspondent à des produits de transpositions en nombres pairs. Ainsi il existe des transpositions σ1, ..., σ2p, τ1, ..., τ2q, tel que φ1 = σ1...σ2p et φ2 = τ1...τ2q. Le produit φ1.φ2 est égal à σ1...σ2p.τ1...τ2q. Comme la somme de 2 nombres pairs est paire le produit est bien une permutation paire. Il reste à montrer que l'inverse de φ1 est bien une permutation paire, cet inverse est égal à σ2p...σ1, le produit des mêmes transpositions pris dans l'ordre inverse.
Dire que An est distingué revient à dire que si φ est élément du sous-groupe et si σ est une permutation quelconque de Sn, alors σ.φ.σ-1 est une permutation paire. En effet, φ est le produit d'un nombre pair de transpositions, et le paragraphe précédent montre que σ-1 se décompose en autant de transpositions que σ. La somme du nombre de toutes ces transpositions est nécessairement paire.
Propriété 3 — L'ordre de An est la moitié de celui de Sn, c'est-à-dire n!/2.
En effet, considérons l'application f de Sn dans Sn qui, à une permutation φ, associe φσ. Ici σ désigne une transposition de Sn. Une telle application est, dans un groupe, appelé translation à droite. La fonction f, comme toute translation, est une bijection. L'image de An est incluse dans l'ensemble des permutations impaires. La bijection de f montre que l'ordre de An est plus petit que le cardinal de l'ensemble des permutations impaires. De même l'image par f d'une permutation impaire est paire, la bijection de f montre aussi que le cardinal de l'ensemble des permutations impaires est plus petit que celui des permutations paire, c'est-à-dire l'ordre de An. Il y a égalité entre l'ordre de An et le cardinal de l'ensemble des permutations impaires. Ces deux ensembles forment une partition de Sn de 2 sous-ensembles de même cardinal, ce qui termine la démonstration.
Propriété 4 — Soit m, un entier plus petit que n. Un cycle de Sn et de longueur m est élément du groupe alterné si, et seulement si, m est impair.
Une petite récurrence vient à bout de la démonstration de cette propriété. Si n est égal à 2, comme une transposition est impaire, la propriété est vérifiée. Supposons la propriété vraie à l'ordre m - 1 et étudions la parité d'un cycle le longueur m, noté (a1...am-1am). On remarque que le cycle est produit de la transposition (am-1am) et du cycle (a1...am-1). L'hypothèse de récurrence montre que le cycle de longueur m une permutation paire si et seulement si m - 1 est paire, ce qui termine la démonstration.
Signature
Article détaillé : signature d'une permutation.La signature d'une permutation est la parité du nombre d'inversions contenues dans une permutation. On démontre que cette application est un morphisme de groupe de Sn dans {-1, 1} et que la signature d'une transposition est toujours égale à -1. On en déduit que le nombre de transpositions nécessaire pour décomposer une permutation ne peut à la fois être paire et impaire, sinon la signature ne serait pas un morphisme de groupe. En effet, si φ est une permutation qui se décompose en p ou bien q transpositions, la signature de φ, d'après la propriété de morphisme est à la fois égale à (-1)p et (-1)q, ce qui montre que p et q sont de même parité. On en déduit une nouvelle définition du groupe alterné, équivalente à la précédente :
Définition alternative — Le groupe alterné An est le noyau du morphisme signature du groupe symétrique Sn[5].
Cette approche offre des démonstrations alternatives aux propositions du paragraphe précédent numérotées de 2 et 3. Le noyau d'un morphisme est toujours un sous-groupe distingué, ce qui montre que An est un sous-groupe distingué. L'ordre du noyau que multiple l'ordre de l'image d'un morphisme de groupe est égal à l'ordre du groupe de départ, ce qui permet de déterminer l'ordre du groupe alterné.
Exemples
Le groupe alterné de degré 2 ne contient que l'élément neutre.
Le groupe symétrique de degré 3 est d'ordre 6 et contient : l'identité, trois transpositions et deux cycles d'ordre 3. Le groupe alterné de degré 3 ne comporte que l'identité et les cycles d'ordre 3 :

Comme tout groupe contenant 3 éléments, il est isomorphe au groupe cyclique d'ordre 3.
Le groupe symétrique de degré 4 est d'ordre 24, le groupe alterné associé est d'ordre 12. Il contient les cycles d'ordre 3 et les produits de 2 cycles d'ordre 2 de supports disjoints :

Le groupe alterné de degré 4 n'est pas abélien. Pour s'en rendre compte, il suffit de remarquer que les cycles (1 2 3) et (2 3 4) ne commutent pas. Aucun groupe alterné de degré supérieur à 4 n'est abélien, car ces groupes contiennent tous une copie de A4, qui ne l'est pas. Le groupe alterné de degré 4 est néanmoins résoluble, il contient un sous-groupe distingué abélien, composé des produits de deux transpositions à support disjoints et de l'élément neutre. Ce groupe est abélien car isomorphe au groupe de Klein et le quotient de A4 par le groupe distingué est aussi abélien car d'ordre 3 et donc cyclique.
Le groupe alterné de degré 5 est d'ordre 60. Il est étudié plus avant à la suite de cet article.
Jeu de taquin
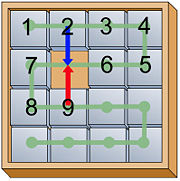
Article détaillé : Taquin.Le jeu de taquin, est un jeu solitaire qui se présente sous la forme d'un damier composé de 15 cases et d'une 16e manquante. Sa théorisation mathématique date de 1879 et se fonde sur les propriétés du groupe alterné[6]. Une des questions posée par Sam Loyd est celle de la résolution du jeu de taquin illustré à droite. Elle correspond à la résolution d'un état du jeu où toutes les cases sont à la bonne position exceptées celles numérotées 14 et 15, qui sont interverties. Elle est impossible si l'on impose à la case vide d'être en bas à droite. Elle l'est si on admet que la case vide soit en haut à gauche et que la première ligne ne contienne que les cases 1, 2 et 3.
Si l'on considère un mouvement comme une permutation des cases numérotées de 1 à 15, alors le groupe des permutations de degré 15 opère sur le jeu de taquin. Pour être plus précis, le groupe qui opère est un sous-groupe engendré par les différentes permutations possibles. Il est relativement simple de vérifier que les permutations engendrant le sous-groupe sont toutes des cycles d'ordre 3 ou 5[7]. Ces permutations sont toutes dans le groupe alterné A15. Le groupe qui opère sur le jeu de taquin est un sous-groupe du groupe alterné A15, qui ne contient aucune transposition. C'est une manière simple de démontrer que la configuration de droite n'est pas résoluble.
D'autres solitaires, comme l'Âne rouge ou le Rubik's cube utilisent de manière analogue le groupe alterné.
Détail de la démonstrationOn numérote une position de la manière indiquée par la figure de droite. Le trou n'est pas compté. Ainsi, la position initiale représentée sur la figure est (123456789...). Le mouvement correspondant à la flèche bleue donne la position (134562789...), elle correspond à la permutation (23456), un cycle d'ordre 5 et donc impair. Celle correspondant à la flèche rouge donne (123456978...), elle correspond à la permutation (798) un cycle d'ordre 3, encore impair. Si la case vide est sur un bord, on obtient soit la permutation constante soit une d'ordre 7, encore impair. Ainsi toutes les permutations générant le sous-groupe opérant sur le jeu de taquin sont de signatures paires et font ainsi parti du groupe alterné.
La permutation nécessaire à la résolution du cas de figure intitulée Jeu de taquin non résoluble est une transposition, de signature impaire, elle n'est donc pas réalisable car le groupe alterné ne contient aucune transposition.
Avec les notations utilisées, le cas de figure intitulée Jeu de taquin non résoluble correspond à la position 1,2,3,4,8,7,6,5,9,10,11,12,14,15,13. Celle correspondant au taquin reconstitué dans l'ordre avec la case vide en première position à 1,2,3,7,6,5,4,8,9,10,11,15,14,13,12. Passer de l'une à l'autre des positions impose la permutation (47586)(12 15 13), produit de deux permutations de signature paire, donc paire. Il est ainsi possible de résoudre la question posée par Sam Loyd si l'on permet à la case vide de se trouver en haut à gauche.
La référence sur le taquin montre que le groupe alterné A15 est bien celui qui opère sur le jeu.
Classes de conjugaison
Article détaillé : Classe de conjugaison.Structure
La structure des classes de conjugaison est l'un des premiers éléments à étudier dans le cadre d'une analyse d'un groupe non abélien. Elles sont utilisées dans la suite de l'article pour établir que si n est strictement supérieur à 4, le groupe est simple, ou encore que tout groupe simple d'ordre 60 est isomorphe à A5.
Dans un groupe symétrique, les classes de conjugaison sont composées de produits de cycles à supports disjoints de même structure, c'est-à-dire de même nombre et de même longueur. En conséquence, les classes de conjugaison du groupe alterné sont aussi composées de produits de cycles à supports disjoints de même structure, plus précisément :
-
- Une classe de conjugaison est constitué d'éléments ayant la même structure. Si la structure est composée uniquement de cycles de longueurs impaires, où les cycles de longueur 1 sont comptés, sans cycle de même longueur, alors il existe exactement deux classes de conjugaison. Il n'en existe qu'une sinon[8].
Une classe de conjugaison, ou deux dans les cas de A3 et A4, joue un rôle particulier, celle constituée des cycles d'ordre 3 :
-
- Les cycles d'ordre 3 engendrent le groupe alterné.
DémonstrationsÉtablir la nature des classes de conjugaison de An est simplifié par le travail équivalent pour le groupe symétrique. Si φ1 et φ2, désignent deux permutations ayant même structure, la démonstration pour le groupe symétrique montre l'existence d'une permutation σ tel que σ-1φ1σ = φ2. On suppose ici que φ1 et φ2 sont des permutations paires. L'objectif est d'établir quand σ peut être choisi pair et ce qui se passe sinon.
-
- Une classe de conjugaison est constituée d'éléments ayant la même structure. Si la structure est composée uniquement de cycles de longueurs impaires, sans cycle de même longueur, il existe exactement deux classes de conjugaison. Il n'en existe qu'une sinon :
Commençons par établir le cas où il n'existe qu'une classe de conjugaison par structure :
- S'il existe deux entiers distincts invariants par φ2, σ peut être choisi pair. En effet, soit a et b les deux entiers invariant par φ2 et τ la transposition permutant a et b. La transposition τ commute avec φ2, ce qui montre que (σ τ)-1φ1(σ τ) = φ2. Soit σ τ soit σ est pair, ce qui établit la proposition dans ce cas là.
- S'il existe un cycle d'ordre pair dans la décomposition de φ2 en cycles à supports disjoints, σ peut être choisi pair. Ici τ désigne le cycle de φ2 ayant un ordre pair. Une fois encore τ est une permutation impair qui commute avec φ2. Le même raisonnement que précédemment montre que soit σ τ soit σ est pair et permet de conclure.
- S'il existe deux cycles de même longueur et de longueurs différentes de 1, σ peut être choisi pair. Deux cas se présentent, les cycles sont soit pairs soit impairs. S'ils sont pairs, la démonstration précédente permet de conclure. S'ils sont impaires, soient (a1a2...ak) et (b1b2...bk) ces deux cycles. Ici k désigne un entier impair. On définit τ comme égal au produit des k transpositions (a1b1)(a2b2)...(akbk). La permutation τ revient à intervertir les aj avec les bj, elle commute avec φ2. Comme k est un entier impair, la permutation τ est impaire. Le raisonnement précédent permet de conclure.
Établissons le cas où la classe de conjugaison de Sn est divisé en deux :
- Il existe au plus 2 classes de conjugaison pour une structure de cycle donnée. Soit (b1b2...bk) le premier cycle d'ordre différent de 1 de φ2. Soit τ la transposition permutant bk-1 et bk On remarque que φ3 le conjugué de φ2 par τ possède exactement les mêmes cycles que φ2, sauf celui étudié, qui devient (b1b2...bkbk-1). Ainsi, une permutation φ1 de même structure que φ2 est, soit conjuguée à φ2, soit à φ3. Il ne peut donc exister plus de 2 classes de conjugaison.
Le raisonnement pour établir le résultat pour les cycles d'ordre n, si n est impair, est un cas particulier plus simple à comprendre que le cas général. Le lecteur averti peut sauter cette partie de la démonstration.
- Si n est impair strictement supérieur à 1, il existe exactement deux classes de conjugaison contenant des cycles d'ordre n. Pour démontrer cette propriété, il suffit de montrer que (12...n-1n) n'est pas conjugué avec (12...nn-1). Les résultats précédents montrent l'existence d'une permutation impaire, à savoir la transposition σ (n-1 n), tel que le conjugué de (12...n-1n) par σ est égal à (12...nn-1). Si les deux permutations (12...n-1n) et (12...nn-1) sont conjuguées dans le groupe alterné, il existe une permutation τ de signature impaire tel que conjugué de (12...n-1n) par σ τ est égal à (12...nn-1), ce qui revient à dire que τ commute avec (12...nn-1). Autrement dit, si le centralisateur d'un cycle d'ordre n contient une permutation impaire, il n'existe qu'une classe de conjugaison, dans le cas contraire il en existe 2. Démontrer cette propriété revient à montrer que le centralisateur ne contient que des permutations paires. Calculons, dans le groupe symétrique d'indice n, le cardinal de la classe d'un cycle d'ordre n. Tout élément de la classe s'écrit (1ψ(2)ψ(3)...ψ(n)) où ψ désigne une permutation de l'ensemble des entiers compris entre 2 et n. Il existe (n - 1)! permutations de cette nature. L'ordre du centralisateur du cycle que multiplie le cardinal de sa classe est égal à l'ordre du groupe symétrique , ce résultat est connu sous le nom de formule de Burnside (cf Action par conjugaison). On en déduit que l'ordre du centralisateur est égal à n. Les n premières puissances du cycle sont des éléments distincts du centralisateur, le centralisateur est le groupe cyclique composé des puissances du cycle car il contient exactement n éléments. Ce groupe cyclique est composé de produits de permutations paires et ne contient que des permutations paires. Il ne peut donc exister de permutation τ de signature impaire dans le centralisateur du cycle, ce qui établit la propriété.
Le raisonnement du cas général est de même nature que le cas précédent :
- Si la structure n'est pas celle de l'un des cas où il est établi qu'il existe une unique classe de conjugaison, alors il en existe deux. En effet, soit φ une permutation de An qui ne correspond pas à l'un des cas où il est établi que qu'il existe une unique classe de conjugaison. Démontrer cette propriété revient à montrer que le centralisateur Gφ de φ, dans Sn ne contient que des permutations paires. Soient γ1, γ2, ..., γp les cycles à supports disjoints dont le produit est égal à φ et n1, n2, ..., np l'ordre des différents cycles. On suppose de plus que la suite des nj est strictement décroissante. Comme on compte aussi les cycles d'ordre 1, la somme des nj, où j varie de 1 à p, est égale à n. Le sous groupe de Sn engendré par les différents cycles γj est inclus dans Gφ. L'objectif est de montrer que ce groupe est exactement égal à Gφ. C'est un groupe abélien d'ordre le produit des nj pour j variant de 1 à p. Il suffit de montrer que le cardinal Cφ de la classe de conjugaison de φ est égal à n! que divise le produit des nj. Le fait que l'ordre de Gφ que multiplie Cφ soit égal à l'ordre de Sn, c'est-à-dire n! permet de conclure. Calculons dans un premier temps Np, le nombre de manières possibles de partitionner un ensemble de n éléments en p sous-ensembles tel que le jième contienne nj élément. On raisonne par récurrence. On peut supposer p supérieur ou égal à 2 car le cas où p est égal à 1 est traité dans le paragraphe précédent. On veut montrer que :

- Si p est égal à 2, comme n1 ne peut être égal à n2, la formule est vérifiée et correspond à celle du coefficient binomial. Dans le cas général, on trouve que Np est égal à Np-1 que multiplie le nombre de manières de partitionner un ensemble de n éléments en deux parties dont l'une contient np éléments. Comme la somme des n - np est différente de np, l'hypothèse de récurrence montre que :

- Il a été établi qu'il existe exactement (nj - 1)! cycles d'ordre nj, ce qui montre que :

- Le fait que l'ordre de Gφ que multiplie Cφ soit égal à n! montre que l'ordre de Gφ est bien égal au produit des nj, ce qui est exactement l'ordre du groupe engendré par les cycles γi. Le deuxième groupe est inclus dans le premier et leurs ordres sont égaux. On en conclut qu'ils sont égaux. Chaque cycle est de signature paire car l'ordre des cycles est impair. Le produit de permutations de signatures paires est de signature paire, Gφ ne contient que des permutations de signature paire. Un raisonnement analogue à celui du cas du cycle d'ordre n permet de conclure.
La démonstration du fait que les cycles d'ordre 3 engendrent le groupe alterné est comparable à un jeu de taquin.
-
-
- Les cycles d'ordre 3 engendrent le groupe alterné.
-
- Soit φ une permutation du groupe alterné An. On construit une suite σk pour k variant de 1 à n - 2 tel que φσ1σ2...σn-2 soit égal à l'identité. On remarque alors que σn-2-1...σ2-1σ1-1 est un produit de cycles d'ordre 3 égal à φ. On raisonne par récurrence, si φ(1) est égal à 1 alors σ1 est l'identité, sinon, σ1 est le cycle (1φ-1(1)x1), où x1 est un entier compris entre 2 et n et différent de φ-1(1). On a φσ1(1) = φφ-1(1) = 1.
- On suppose, par hypothèse de récurrence, que φσ1σ2...σj-1 laisse invariant les entiers compris entre 1 et j - 1 et on construit un cycle σj tel que φσ1σ2...σj laisse invariant les entiers compris entre 1 et j. Ici, j désigne un entier inférieur à n - 2. Si φ(j) est égal à j, σj est l'identité sinon σj = (j (φσ1σ2...σj-1)-1(j) xj), ici xj désigne un entier différent de (φσ1σ2...σj-1)-1(j) et strictement supérieur à j, qui existe nécessairement. Comme, par hypothèse de récurrence, la restriction de φσ1σ2...σj-1 aux entiers compris entre 1 et j - 1 est l'identité, φσ1σ2...σj-1(j) est plus grand que j - 1 et σj laisse aussi invariant les j - 1 premiers entiers. Un calcul analogue à celui de σ1(1) montre que la restriction aux entiers compris entre 1 et j de φσ1σ2...σj est l'identité.
- La permutation φσ1σ2...σn-2 est un produit de permutations paires, elle est donc paire. La construction des σk montre que φσ1σ2...σn-2, est soit la transposition (n n-1), soit l'identité. Comme une transposition est impaire, la permutation est bien l'identité, ce qui termine la démonstration.
Exemples
La seule classe de conjugaison de S4 qui se trouve divisée en deux dans A4 est celle des cycles d'ordre 3. Un tel élément est en effet composé de deux cycles de longueurs impaires et différentes : 1 et 3. Les cycles d'ordre 1 sont en effet comptés. La classe de l'élément neutre ne contient qu'un élément et n'est jamais divisée. Celle des permutations composées de deux transpositions à supports disjoints n'est pas divisée en deux, car une telle permutation contient des cycles de longueurs paires ou encore car elle contient deux cycles de même longueur. On obtient 4 classes de conjugaison : l'identité, les produits de deux cycles disjoints d'ordre 2 et deux classes de cycles d'ordre 3 :


Dans le cas de A5, il est plus long d'écrire toutes les classes en extension, on trouve en effet 60 éléments. Il existe 5 classes de conjugaison. Une contient l'identité, une autre 15 permutations formées de deux transpositions à supports disjoints. Cette classe n'est pas divisée car elle contient un cycle de longueur paire. Les 20 cycles d'ordre 3 ne forment plus qu'une classe de conjugaison. Ils sont maintenant complétés par deux cycles de même longueur, ceux d'ordre 1. Enfin, les cycles d'ordre 5 sont divisés en 2 classes de conjugaisons contenant 12 permutations chacune[9].
Groupe simple
Article détaillé : Groupe simple.Simplicité et groupe alterné
Une propriété éventuelle et importante d'un groupe est d'être simple, ce qui signifie qu'il ne contient pas de sous-groupe distingué propre.
-
- Si n est un entier supérieur ou égal à 5, le groupe alterné de degré n est simple[10].
Les groupes alternés forment une deuxième série infinie de groupes simples, après ceux, abéliens et d'ordre un nombre premier. Cette série contient le plus petit groupe simple non commutatif :
-
- Le groupe alterné de degré 5 est le plus petit groupe simple non abélien et tout groupe simple d'ordre 60 est isomorphe à A5[11].
La structure de groupe alterné intervient par exemple dans la résolution d'une équation algébrique par radicaux, à travers la proposition suivante :
-
- Si n est un entier supérieur ou égal à 5, le seul sous-groupe distingué et propre de Sn est An[12].
Démonstrations-
- Si n est un entier supérieur ou égal à 5, le groupe alterné de degré n est simple :
La méthode proposée ici est peu technique et n'utilise pas les théorèmes de Sylow. Il existe d'autres démonstrations plus courtes, particulièrement pour n égal à 5 se fondant sur les théorèmes cités[13].
Dans un premier temps, démontrons le lemme suivant :
-
- Soit H un sous-groupe distingué du groupe alterné An. Si H n'est pas réduit à l'élément neutre, il contient un cycle d'ordre 3 :
- Puisque H n'est pas réduit à l'élément neutre, nous pouvons choisir dans H un élément σ distinct de l'élément neutre.
- Supposons tout d'abord que la décomposition en cycles de supports disjoints de σ ne contienne pas uniquement des cycles d'ordre 3. Montrons qu'il existe une partie E à 3 éléments de {1, 2,... n} telle que F, l'union de E et de σ(E), contienne exactement 4 éléments. S' il existe dans la décomposition de σ au moins un cycle (a1 a2 a3 a4...) d'au moins quatre éléments, il suffit de définir E comme égal à {a1, a2, a3}. S'il n'en existe pas, il n'existe que des cycles d'ordre 2 et 3. Puisque nous supposons que la décomposition de σ ne contient pas uniquement des cycles d'ordre 3, il existe au moins un cycle d'ordre 2, donc il en existe au moins deux (a1 a2) et (b1 b2), sinon la signature de σ serait égale à -1 et σ ne serait pas dans le groupe alterné. Il suffit alors de définir E comme égal à {a1, a2, b1}.
- Choisissons un cycle γ de support E. C'est un cycle de longueur 3 et, en particulier, une permutation paire. Le support de σγσ-1 est égal à σ(E) et est donc distinct du support E de γ, donc les permutations σγσ-1 et γ sont distinctes, donc σγσ-1γ-1 est distincte de l'élément neutre. D'autre part, σγσ-1γ-1 s'écrit encore comme le produit de σ par un conjugué de σ-1 dans An; comme H est un sous-groupe distingué de An, σγσ-1γ-1 appartient donc à H et, d'après ce qui précède, à H-{1}. Comme le support de γ-1 est E et que le support du produit de deux permutations est contenu dans la réunion de leurs supports, le support de σγσ-1γ-1 est inclus dans F. Puisque F n'a que quatre éléments et que σγσ-1γ-1 est une permutation paire distincte de l'élément neutre, σγσ-1γ-1 est soit un cycle d'ordre 3, soit un produit de deux transpositions à supports disjoints. Nous avons donc prouvé que si la décomposition canonique de σ n'est pas formée uniquement de cycles d'ordre 3, H comprend soit un cycle d'ordre 3, soit un produit de deux transpositions à supports disjoints.
- Supposons maintenant que σ ne contienne que des cycles d'ordre 3. S'il n'en contient qu'un, σ est un cycle d'ordre 3 et la proposition est démontrée. Sinon, σ contient au moins 2 cycles d'ordre 3, que l'on note (a1 a2 a3) et (b1 b2 b3). Si γ désigne la permutation composée des deux transpositions (a1 b1) et (a2 b2), le produit σγ-1σ-1γ est le produit de σ par un conjugué de σ-1 dans An, il est donc élément de H. Ce produit est une permutation composée des 2 transpositions : (a1 b1) et (a3 b3). (Pour le montrer, noter que σγ-1σ-1, étant le conjugué de γ-1 = γ par σ, est égal à (σ(a1) σ(b1)) (σ(a2) σ(b2)) = (a2 b2) (a3 b3).)
- Pour conclure, il suffit de montrer que si H contient une permutation π composée de 2 transpositions à supports disjoints (a1 a2)(b1 b2), alors H contient un cycle d'ordre 3. Comme n est supérieur ou égal à 5, il existe un élément c qui n'est pas dans le support des deux transpositions. On considère γ, la permutation alternée (a1 a2 c). Par exemple en notant que πγπ-1 est la conjuguée de γ par π et est donc égale à (π(a1) π(a2) π(c)) = (a2 a1 c) = γ-1, on voit que πγπ-1γ-1 est un élément de H égal au cycle γ-2 = γ = (a1 a2 c), ce qui permet de conclure.
Nous avons donc prouvé notre lemme, à savoir que si n est au moins égal à 5, tout sous-groupe distingué de An non réduit à l'élément neutre comprend au mois un cycle d'ordre 3. Une fois ce lemme établi, il suffit de prouver que le seul sous-groupe distingué de An qui comprenne un cycle d'ordre 3 est An lui-même. Puisque An est engendré par les cycles d'ordre 3, il suffit de prouver que si H est un sous-groupe distingué de An qui comprend un cycle d'ordre 3, H comprend tous les cycles d'ordre 3. Pour cela, on peut par exemple prouver que si n est au moins égal à 5, deux cycles d'ordre 3 sont toujours conjugués dans An (et non seulement dans Sn.) Soient (a b c) et (x y z) deux cycles d'ordre 3. On sait qu'il existe une permutation σ telle que (x y z) = σ (a b c) σ-1. Si la permutation σ est paire, notre argument est vrai. Sinon, choisissons dans {1, ... n} deux éléments u, v distincts de x, y et z (ce qui est possible puisque n est au moins égal à 5). En conjuguant l'égalité (x y z) = σ (a b c) par (u v), nous trouvons que (x y z) est le conjugué de (a b c) par la permutation paire (u v) σ, et notre argument est encore vrai.
(Remarque : même si n n'est pas supposé au moins égal à 5, il est encore vrai que le seul sous-groupe distingué de An qui comprenne un cycle d'ordre 3 est An lui-même. En effet, on prouve facilement que si γ1 et γ2 sont des cycles d'ordre 3 dans An, un au mois des deux cycles γ2 et γ2-1 est conjugué de γ1 dans An et non seulement dans Sn.)
-
- Le groupe alterné de degré 5 est le plus petit groupe simple non abélien :
Dans un premier temps, utilisons un théorème de Burnside stipulant qu'un groupe simple non abélien possède un ordre dont la décomposition en facteurs premiers contient au minimum 3 nombres premiers. Les seuls entiers inférieurs à 60 vérifiant cette propriété sont 30 et 42.
Un groupe de 30 éléments n'est jamais simple, les théorèmes de Sylow permettent de le démontrer. Le premier montre l'existence d'un sous-groupe d'ordre 5 et d'un autre d'ordre 3. Les sous-groupes d'ordre 5 ont pour intersection deux à deux l'élément neutre car tout élément non neutre d'un sous-groupe engendre l'intégralité du sous-groupe. Deux autres théorèmes de Sylow montrent que si a est le nombre de sous-groupes d'ordre 5, a est un diviseur de 6 congru à 1 modulo 5. Il existe deux valeurs possibles, 1 et 6. Supposons qu'il n'existe qu'un unique sous-groupe d'ordre 5, tout conjugué d'un élément d'ordre 5 est aussi un élément d'ordre 5, donc un élément du sous-groupe et le sous-groupe est distingué. S'il existe 6 sous-groupes d'ordre 5, le groupe entier contient 24 éléments d'ordre 5. On raisonne alors sur les sous-groupes d'ordre 3. Un raisonnement analogue montre que si b est le nombre de sous-groupes d'ordre 3, b divise 10 et est congru à 1 modulo 3. Il en existe donc soit 1 soit 10. S'il en existait 10, on trouverait 20 éléments d'ordre 3, ce qui est incompatible avec l'existence de 24 éléments d'ordre 5. Les deux uniques éléments d'ordre 3 et l'identité forme alors un sous-groupe distingué.
Un raisonnement analogue montre qu'un groupe d'ordre 42 n'est jamais simple. La lettre a désigne maintenant le nombre de sous-groupes d'ordre 7. On sait que a est un diviseur de 6 congru à 1 modulo 7. Il n'existe qu'un unique sous-groupe d'ordre 7, nécessairement distingué.
-
- Si n est un entier supérieur ou égal à 5, le seul sous-groupe distingué et propre de Sn est An :
Soit H un sous-groupe distingué de Sn. L'intersection de H et du groupe alterné est, soit le groupe alterné, soit l'élément neutre. En effet, le groupe alterné est simple et n'admet pas de sous-groupe distingué non trivial. L'ordre du groupe alterné est égal à la moitié de celui du groupe symétrique.
Si H contient le groupe alterné, comme son ordre divise celui du groupe symétrique (le théorème de Lagrange) et que le groupe alterné est la moitié de celui du groupe symétrique, H est soit le groupe alterné, soit le groupe symétrique. Si H ne contient pas le groupe alterné il ne peut pas contenir plus de deux éléments. En effet, soit a et b deux éléments non neutres de H, leur signature est impaire, leur produit est donc dans le groupe alterné et est l'élément neutre. On en déduit que b est l'inverse de a, le même raisonnement montre que a2 est aussi l'élément neutre, donc a est égal à b, ce qui montre bien qu'il n'existe au plus qu'un élément de H non neutre. Cet élément fait partie d'une classe de conjugaison ne contenant qu'un unique élément car H est distingué. La seule classe de conjugaison réduite à un élément est celle de l'élément neutre, ce qui montre que H est réduit à un élément.
Exemple
Article détaillé : Théorème d'Abel (Algèbre).Si le groupe de Galois d'un polynôme irréductible sur un corps parfait comme Q, celui des nombres rationnels, n'est pas résoluble, alors les racines du polynômes ne s'expriment pas à l'aide de radicaux. Tel est le contenu de la version formulée par Evariste Galois et en langage moderne, du théorème d'Abel. Les exemples les plus simples s'obtiennent à l'aide d'équation du cinquième degré dont le groupe de Galois est le groupe symétrique S5. Un tel groupe ne contient qu'un unique sous-groupe distingué propre, son groupe alterné. Il n'est donc pas résoluble.
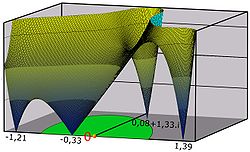
Le polynôme à coefficients dans Q : P(X) = X5 - 3X - 1 est un exemple de polynôme de cette nature, ce qui se démontre relativement simplement. Ce polynôme est illustré sur la figure de droite, plus précisément cette figure illustre la nappe qui à un nombre complexe z associe le module de P(z) pour les points de coordonnée imaginaire positive. On remarque que l'équation associée possède 5 racines dont trois réelles, de valeurs approximatives -1,21 -0,33 et 1,39 et deux imaginaires 0,08 + 1,33.i et son conjugué 0,08 - 1,33.i. Le fait qu'il n'existe qu'une unique racine dans le disque unité, illustré en vert sur la figure, montre que le polynôme est irréductible dans Q et que le groupe contient un élément d'ordre 5. L'existence d'un unique couple de racines imaginaires conjuguées montre l'existence d'une transposition dans le groupe. Ces deux propriétés établissent que le groupe de Galois est isomorphe à S5, qui n'est pas résoluble d'après les résultats précédents[14].
- Remarque 1 : Il est impropre de dire que l'équation P(z) = 0 n'est pas résoluble. Cette équation possède 5 racines qui s'approximent aussi précisément qu'on le souhaite et qui s'expriment exactement à l'aide d'intégrales elliptiques. En revanche, ces racines ne peuvent s'exprimer à l'aide des quatre opérations et de radicaux, ce qui démontre qu'il n'est pas possible de trouver une expression des racines dans le cas général d'une équation du cinquième degré, comme on peut le faire pour les équations de degré 1, 2, 3 ou 4.
- Remarque 2 : Les groupes simples non abéliens qui interviennent dans les groupes de Galois ne sont pas nécessairement des groupes alternés. Il existe ainsi un polynôme de degré 7 ayant pour groupe de Galois un groupe simple d'ordre 168. En revanche, si un polynôme de degré 5 n'est pas résoluble, cela signifie nécessairement que le groupe de Galois contient comme sous-groupe distingué le groupe alterné de degré 5.
Détails de la démonstration-
- Le polynôme P(X) est irréductible dans Q[X] :
Montrons d'abord que le polynôme P(X) admet une unique racine dans le disque de centre 0 et de rayon 1. Pour s'en rendre compte, il suffit d'observer la figure de droite. Il est aussi possible de remarquer que si z parcourt le cercle unité des nombres complexes, la variable P(z) parcourt un tour autour de l'unité. En effet :

Le théorème des résidus montre l'existence et l'unicité d'une racine dans le disque unité.
Montrons ensuite que le polynôme P(X) admet exactement trois racines réelles. Pour cela, le théorème des valeurs intermédiaires ainsi que le calcul des valeurs du polynôme en -2, -1, 0 et 2 montre l'existence d'au moins trois racines réelles. La dérivée du polynôme, égale à 5X4 - 3, possède exactement deux racines, ce qui montre l'existence d'au plus trois racines réelles.
Le polynôme est irréductible. En effet, s'il ne l'était pas, il serait le produit de deux polynômes à coefficients dans Z car Z[X] est un anneau factoriel. Les deux coefficients dominants ainsi que les deux constantes de ces polynômes seraient égaux à 1. Ceci est contraire au fait que l'un des polynômes contient uniquement des racines de module strictement supérieur à 1.
-
- Le polynôme P(X) est irréductible dans Q[X] (seconde méthode) :
Une méthode plus manuelle consiste à rechercher les diviseurs possibles de P(X) dans Q[X]. Le caractère factoriel de l'anneau Z[X] montre que si le poynôme est réductible dans Q[X], il l'est aussi dans Z[X] (cf l'article Anneau factoriel). Le polynôme n'admet pas de racine entière, on en déduit qu'il n'existe pas de diviseur de degré 1 ou 4 dans Z[X].
Recherchons un diviseur de degré 2 ou 3. S'il en existe un, alors il existe deux entiers a et b, avec b=±1, tels que :

Le calcul du terme d'ordre 1 montre que a(a+1)=2b, c'est-à-dire b=1 et a=1 ou -2, ce qui est incompatible avec le calcul du terme d'ordre 2, a3+2ab-b=0.
On en déduit qu'il n'existe aucun diviseur de degré 2 ou 3 de P(X) dans Z[X], ce qui montre son irréductibilité dans Z[X].
-
- L'équation P(X) = 0 n'est pas résoluble par radicaux dans Q, l'ensemble des nombres rationnels :
Soit G le groupe de Galois du corps de décomposition K du polynôme. G opère sur les racines du polynôme, on en déduit que G s'identifie à un sous-groupe de S5 car les racines du polynôment engendre K, considéré comme une extension de Q. La conjugaison complexe est un automorphisme de K laissant invariant Q et permutant les deux racines complexes, on en déduit que G contient une transposition.
Montrons que G contient un élément d'ordre 5. Soit α une racine de P, le rapport entre l'ordre du groupe G et le cardinal du stabilisateur de α est égal au cardinal de l'orbite de α (cf Action de groupe (mathématiques)). Comme le polynôme P est irréductible, l'orbite de α est l'ensemble des 5 racines (cf Corps de décomposition). Ceci montre que l'ordre de G est un multiple de 5. Le théorème de Cauchy montre que G contient un élément d'ordre 5.
Montrons que G est isomorphe à S5. Les seuls éléments d'ordre 5 étant des cycles d'ordre 5, G en contient un. Or le groupe symétrique d'ordre 5 est engendré par tout couple composé d'une transposition et d'un élément d'ordre 5. Le groupe de Galois est en conséquence isomorphe à S5.
Le groupe de Galois contient un unique sous-groupe distingué propre A5. Ce sous-groupe est simple et non abélien, en conséquence, le groupe de Galois n'est pas résoluble. Le théorème d'Abel montre que l'équation polynomiale n'est pas résoluble par radicaux.
Représentation
Caractère
Article détaillé : Caractère d'une représentation d'un groupe fini.Une manière d'étudier un groupe G est de le représenter à l'aide d'un sous-groupe d'un groupe linéaire. Le cas le plus simple est celui où le corps de l'espace vectoriel est celui des nombres complexes. Certaines représentations sont particulièrement digne d'intérêt, on les appelle les représentations irréductibles, elles ne possèdent pas de sous-espaces stables par la représentation autre que l'espace entier et celui réduit au vecteur nul.
Le caractère d'une représentation est l'application qui à un élément du groupe associe la trace de son endomorphisme. Si la représentation φ est irréductible, son caractère χφ est de norme 1, pour la norme définie par le produit hermitien suivant, où g est le cardinal du groupe G :

Les caractères de deux représentations irréductibles non isomorphes sont orthogonaux et si χi désignent les différents caractères des représentations irréductibles et e l'élément neutre du groupe G, alors :

Groupe alterné de degré 4
Un premier caractère irréductible est donné par la représentation triviale t dans un espace de dimension 1. À chaque élément de A4 cette représentation associe l'automorphisme identité, le caractère χt de cette représentation associe 1 à chaque élément du groupe A4.
On obtient une deuxième représentation φ par restriction de la représentation φ1 de S4 aux éléments de A4, en utilisant les notations de l'article Représentations du groupe symétrique d'indice quatre. Comme la valeur d'un caractère ne dépend pas du choix d'un élément pris dans une même classe de conjugaison, le caractère est défini par χφ(e) = 3, χφ(ab)(cd) = -1 et χφ(abc) = 0. Un calcul montre que la norme de cette représentation est égale à 1, elle est donc irréductible.
Il existe un morphisme de A4 dans le groupe cyclique d'ordre 3. Il existe deux représentations irréductibles du groupe cyclique d'ordre 3 qui sont toutes deux de dimension 1. La première associe j, la racine cubique de l'unité de partie imaginaire strictement positive, à un élément d'ordre 3 et la deuxième associe son conjugué à la même valeur.
L'égalité (1) montre qu'il n'existe pas d'autre représentation irréductible, à un isomorphisme près. En effet, 32 + 12 + 12 + 12 est égal à 12, l'ordre du groupe alterné de degré 4. On en déduit la table des caractères[15] :
Car. irr. 1 (ab)(cd) (abc) (acb) t 1 1 1 1 σ1 1 1 j j2 σ2 1 1 j2 j φ 3 -1 0 0 Il existe une représentation de dimension 3. Elle est utilisée dans le paragraphe "Groupe des rotations du tétraèdre".
Groupe alterné de degré 5
Les caractères du groupe alterné de degré 5 sont un peu plus délicats à déterminer que le cas précédent, même s'il est possible d'y parvenir sans utiliser une approche générique plus lourde. L'existence de 5 classes de conjugaison montre qu'il existe 5 représentations irréductibles. La table des caractères est la suivante[16] :
Car. irr. 1 (ab)(cd) (abc) (abcde) (abced) t 1 1 1 1 1 σ1 3 -1 0 1/2.(1 + √5) 1/2.(1 - √5) σ2 3 -1 0 1/2.(1 - √5) 1/2.(1 + √5) φ 4 0 1 -1 -1 ψ 5 1 -1 0 0 Les caractères de ces représentations sont tous réelles. Chacune de ces représentations s'incarne sur un espace vectoriel réel (cf Caractère d'une représentation d'un groupe fini). Cette remarque s'applique, en particulier, sur les représentations de dimension 3. Le paragraphe "Groupe des rotations du dodécaèdre" montre qu'une telle représentations correspond à un groupe de symétrie d'un solide de Platon.
Calcul de la tableIl n'existe pas de morphisme non trivial de A5 dans un groupe cyclique. En effet, le noyau d'un tel morphisme est un groupe distingué, c'est-à-dire soit l'élément neutre soit le groupe A5. Comme le groupe A5 n'est pas abélien, le morphisme ne peut être injectif et si le noyau n'est pas l'élément neutre, c'est le groupe entier. Cette remarque permet d'élucider rapidement la nature des représentations de degré 1 et 2.
-
-
- La seule représentation irréductible de degré 1 ou 2 est la représentation triviale :
-
- Une représentation de degré 1 est un morphisme de A5 dans un groupe cyclique sous-groupe des racines de l'unité des nombres complexes, la remarque précédente permet de conclure. Pour le degré 2, l'application qui à un élément de A5 associe le déterminant de sa représentation est aussi un morphisme à valeur dans un groupe cyclique sous-groupe des racines de l'unité des nombres complexes. Un tel déterminant est égal à 1, en dimension 2, cela signifie que les deux valeurs propres sont conjugués et que le caractère est à valeurs réelles. Une représentation dont le caractère est à valeurs réelles est réelle. Or en dimension 2, les seules isométries de déterminant égal à 1 sont les rotations. L'ensemble d'arrivé est encore un groupe cyclique, la représentation est encore triviale.
Il existe autant de représentations irréductibles que de classes de conjugaison. Dans le cas de A5 il en existe 5. Avoir déterminer les représentations de degré 1 et 2 permet de calculer la dimension de chacune de ces représentations.
-
-
- Les représentations irréductibles ont pour degré respectifs 1, 3, 3, 4 et 5 :
-
- L'égalité 1 montre que l'ordre de A5 est égal à la somme des carrés des différentes représentations irréductibles. Si l'on néglige la représentation triviale, la somme des carrés des différents degrés est égale à 59. Il suffit pour établir le résultat de déterminer le nombre de manière de décomposer 59 en somme de 4 carrés. Comme aucun carré ne peut être égal à 4, il n'existe qu'une unique possibilité 3, 3, 4 et 5.
-
-
- Le caractère de degré 4 est égal à (4, 0, 1, -1, -1) :
-
- Pour le construire, on utilise une technique analogue à celle de la représentation régulière. On fait opérer le groupe alterné sur une base de l'espace et on prolonge les applications obtenues par linéarité. Le caractère associé est (5, 2, 1, 0, 0). La représentation contient un espace propre de dimension 1 associé à la représentation triviale. Il correspond à la droite vectoriel dirigé par la somme des 5 éléments de la base. En retranchant cette représentation on obtient une nouvelle représentation dont le caractère est égal à la différence du caractère précédent et du caractère trivial, soit (4, 1, 0, -1, -1). Il suffit de vérifier que sa norme est égale à 1 pour conclure sur l'irréductibilité de la représentation associée.
-
-
- Calcul des deux caractères σ1 et σ2 de degré 3:
-
- Les éléments de la deuxième classe de conjugaison sont d'ordre 2, les valeurs propres associées sont nécessairement 1 ou -1, ce qui donne pour valeurs possibles du caractère : 3, 1, -1, -3. La norme du caractère est égal à 1, ce qui limite à 1 et -1 les valeurs possibles, puis comme le déterminant est égal à 1, on ne trouve que -1. Pour la troisième valeur, il suffit de calculer le produit scalaire du caractère avec la somme de ceux de degré 1 et 4, on trouve 0 pour les deux caractères. Si τ est une permutation dans une des deux dernières classes, τ et τ-1 sont éléments de la même classe, or les caractères de τ et celui de τ-1 sont conjugués, ce qui montre qu'ils sont réels. Le calcul de la norme montre que la somme des carrés des deux dernières valeurs du caractère est égale 3/2 et le produit scalaire avec le caractère trivial montre que leur somme est égale à 1. On trouve 1/2.(1 + √5) et 1/2.(1 - √5).
-
-
- Le caractère de degré 5 est égal à (5, 1, -1, 0, 0) :
-
- On connait le caractère de la représentation régulière et on sait qu'il est composé de p représentations irréductibles de degré p. On en déduit la valeur du dernier caractère.
Groupe des rotations d'un polyèdre régulier
Représentation et géométrie
Les groupes A4 et A5 admettent des représentations de dimension 3 réelles. Ces représentations sont composées d'automorphismes qui peuvent être vus comme des isométries si l'espace vectoriel E de dimension 3 est équipé du bon produit scalaire. En effet, si G est le groupe des automorphismes, et (.|.) un produit scalaire quelconque de E, alors le produit scalaire <., .> suivant confère le statut d'isométrie aux éléments de G :

Ici, |G| désigne l'ordre du groupe G. Un élément de G est une isométrie car la translation à droite est une bijection. Ainsi, si h est un élément de G, l'ensemble des éléments g.h, si g décrit G, est exactement le groupe G.
Ces isométries sont toutes des rotations car leur déterminant est égal à 1. Pour n égal à 4, il suffit de remarquer que la représentation est obtenue par restriction d'une représentation de S4, chacune des isométries étant le produit d'un nombre pair d'images de transpositions de déterminant égal à -1. Pour n égal à 5, la preuve est donné dans la construction de la table.
Les représentations de degré 3, pour n égal à 4 ou 5, sont fidèles, c'est-à-dire qu'elles sont injectives. Pour s'en persuader, il suffit de remarquer que ces représentations possèdent des caractères qui ne prennent la valeur 3 que pour l'identité (qui est l'image de l'élément neutre). Ces différentes propriétés permettent de concevoir ces représentations de dimension 3 comme des groupes de rotations d'un polyèdre régulier.
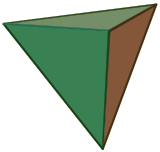
Groupe des rotations du tétraèdre
Si n est égal à 4, la représentation est obtenue en restreignant une représentation irréductible de degré 3 du groupe symétrique, décrite dans l'article Représentations du groupe symétrique d'indice quatre. Le groupe G est engendré par les deux automorphismes ayant les matrices suivantes dans une base orthonormale :

Soient φ234 l'automorphisme de matrice M234 et s un vecteur non nul de l'axe de la rotation φ234. On peut, par exemple choisir s comme le point de coordonnées (1, 1, 1). Soit S l'orbite de s, c'est-à-dire l'ensemble des points g(s), si g parcourt le groupe G. L'ensemble S est globalement stable par l'action de G. On définit le polyèdre comme l'enveloppe convexe de S, qui fournit les sommets du polyèdre recherché. Ce polyèdre est un tétraèdre régulier et son groupe des rotations est exactement égal à G.
Détails de la démonstration-
- Le polyèdre contient 4 sommets :
La formule de Burnside (cf Action de groupe (mathématiques)) indique que le cardinal de S est égal à l'ordre de G que divise l'ordre du stabilisateur de s. Le stabilisateur de s est le sous-groupe de G composé des éléments laissant invariant s. Le stabilisateur contient au moins trois éléments : l'identité, φ234 et le carré de φ234. Il n'en contient pas d'autre. En effet, si g est un élément de G, différent d'une puissance de φ234 et admettant s comme point fixe alors le sous-groupe laissant s fixe est cyclique d'ordre strictement supérieur à 3. Un tel sous-groupe n'existe pas dans G. On en déduit que S est un ensemble à 4 éléments, c'est-à-dire : 12 l'ordre de G, que divise 3 l'ordre du stabilisateur de s.
-
- Le polyèdre est globalement invariant par l'action de G :
Le tétraèdre T, dont les sommets forment l'ensemble S, est globalement invariant par G. En effet, les sommets le sont, les arêtes le sont aussi car si s1 et s2 sont deux segments, l'image du segment [s1, s2] par un élément de G est un segment d'extrémités deux éléments de S. Le même raisonnement s'applique encore pour les faces et l'intérieur du polyèdre.
-
- Le polyèdre est régulier :
Le tétraèdre T est régulier. Pour s'en rendre compte, considérons un point quelconque t de S. Son orbite contient 4 éléments, donc son stabilisateur est d'ordre 3 et il existe une rotation φ de G, laissant invariant t. Il existe un vecteur s1 de S qui n'est pas dans l'axe dirigé par t. En effet, si tous les points de S étaient élément d'une droite vectoriel, cette droite seraient stable par G, la représentation ne serait pas irréductible car contiendrait un espace propre de dimension 1. Les trois points s1, φ(s1) et φ2(s1) forment avec t, l'ensemble S car il contient 4 éléments. Comme φ est une rotation d'axe dirigé par t, les trois points de S différents de t forment un triangle équilatéral. On en déduit que toutes les faces de T sont des triangles équilatéraux, ce qui montre que le tétraèdre T est régulier (ce qui signifie que les arêtes sont toutes de même longueur et que les angles de deux arêtes distinctes partageant un même sommet sont aussi tous égaux).
-
- Le groupe des rotations du polyèdre est exactement G :
Le groupe des rotations de T contient G, montrons maintenant qu'il est égal à G. Il existe 4 manière d'envoyer un sommet de S sur un autre sommet, car S contient 4 sommets. Il existe ensuite 3 manières de positionner une arête contenant le sommet s, sans bouger s. Le groupe des rotations de T ne peut donc contenir plus de 12 éléments. Comme G contient exactement 12 éléments, le groupe des rotations de T et G sont confondus.
Groupe des rotations du dodécaèdre
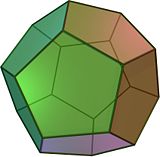 Le groupe des rotations du dodécaèdre régulier est isomorphe à A5.
Le groupe des rotations du dodécaèdre régulier est isomorphe à A5.
 Le groupe des rotations de l'icosaèdre régulier possède la même propriété.
Le groupe des rotations de l'icosaèdre régulier possède la même propriété.
Le groupe A5 possède aussi une représentation irréductible d'ensemble d'arrivée G et de dimension 3. Un raisonnement, analogue à celui du paragraphe précédent, montre que le groupe des rotations d'un dodécaèdre régulier est isomorphe à G. Ceci revient à dire que le groupe des rotations du dodécaèdre régulier est isomorphe au groupe alterné de degré 5.
Le groupe G, qui laisse globalement invariant le dodécaèdre D laisse aussi globalement invariant l'ensemble des centres des faces du dodécaèdre. Le polyèdre, ayant pour sommets les centres des différentes faces de D, est un icosaèdre régulier. Il existe ainsi deux polyèdres réguliers ayant un groupe de rotations isomorphe à A5. La technique consistant à construire un nouveau polyèdre à partir des centres des faces est appelé polyèdre dual. Si un groupe d'isométries laisse invariant un polyèdre, le raisonnement utilisé ici montre qu'il laisse toujours invariant son dual.
Il existe deux manières de procéder. la première suppose connue la structure du dodécaèdre régulier et l'objectif est de montrer que son groupe des rotations est isomorphe à A5. Une méthode simple de procéder est de remarquer qu'il existe 5 cubes de sommets choisis parmi les sommets du dodécaèdre régulier. Le groupe des rotations opère librement sur l'ensemble de ces 5 cubes. Il est donc isomorphe à un sous-groupe de S5. On remarque ensuite que le groupe des rotations contient 60 éléments. En effet, comme le dodécaèdre contient 20 sommets, il existe 20 manières différentes de positionner un sommet. Une fois le sommet positionné, il reste encore trois manière de positionner une arête contenant ce sommet car chaque sommet est élément de trois arêtes. L'ordre du groupe des rotations est 20 que multiplie 3, c'est-à-dire 60. Un sous-groupe de 60 éléments dans S5 est nécessairement distingué car il peut être vu comme le noyau du morphisme qui associe 1 à un élément du sous-groupe et -1 aux autres éléments. Il n'existe qu'un unique sous-groupe distingué non trivial dans S5 c'est A5, ce qui montre l'isomorphisme recherché[17].
Une autre manière de procéder est d'utiliser la représentation de dimension 3 du groupe alterné pour construire le dodécaèdre et en déterminer ses paramètres. Elle est proposée dans la boîte déroulante.
Construction de l'icosaèdre et du dodécaèdreL'objectif est de construire un solide de Platon ayant pour groupe de rotations G formé par les rotations d'une représentation irréductible de degré 3 de A5. Dans un premier temps, il est nécessaire de construire le polyèdre :
-
-
- Il existe un polyèdre convexe P à 12 sommets laissé globalement invariant par G :
-
- On procède comme pour le tétraèdre. Soit φ une rotation d'ordre 5 et s un vecteur propre de φ. On note S l'orbite de s par G, le même raisonnement que pour le tétraèdre montre que le stabilisateur de s est un groupe cyclique d'ordre 5 et que l'orbite est de cardinal 12. Il ne reste plus qu'à montrer que l'orbite de S n'est pas dans un plan. S'il l'était ce plan serait stable ou contiendrait une droite vectoriel stable par tout élément de G. Un tel sous-espace n'existe pas car les éléments de G proviennent d'une représentation irréductible. L'enveloppe convexe de S est un polyèdre P convexe globalement stable par G.
Il faut maintenant montrer que ce polyèdre est l'un des 5 solides de Platon. Pour cela, il suffit de montrer qu'il est régulier.
-
-
- Structure des arêtes autour d'un sommet :
-
- Soient t et s1 deux points distincts de S à une distance minimale d . L'orbite de t contient 12 points, son stabilisateur est, en conséquence, d'ordre 5 et il existe une rotation φ d'ordre 5 ayant pour axe celui dirigé par t. Les images de s1 par les puissances de φ forment un pentagone régulier situé sur un cercle C1 de centre l'intersection du plan contenant le pentagone et de l'axe de la rotation. Ce cercle ne contient pas d'autres points de S. Supposons en effet qu'il contienne un autre point u, il en contient au minimum 5 supplémentaires, formés par l'image de u par les puissances de φ. Il existerait alors au moins 10 points de S sur le cercle C1. Considérons le cercle C2 construit de la même manière , mais cette fois-ci à partir de s1 au lieu de t. Ce cercle contient au moins 5 points de S dont t et uniquement 2 peuvent être aussi des points de l'intersection de C1 et de S. Le cercle C2 contient au moins 2 points de S qui ne sont ni égaux à t ni dans C1. L'ensemble S contiendrait alors au moins 13 points : 10 dans C1, t et deux nouveaux dans C2. C'est absurde car S ne contient que 12 points.
- Il faut encore démontrer que s1 n'est pas dans la direction de t. Comme tous les points de S ont même norme, le seul point possible de S colinéaire est l'opposé -t. Or le point -t n'est pas un candidat pour être le point le plus proche de t. La sphère de rayon la norme de t et de centre le vecteur nul contient au moins 10 points de S, différents de t qui sont dans cette sphère et plus proches de t.
- Le segment [t, s1] est une arête, en effet, si s2 est l'image de s1 par φ et s5 son antécédent, les plans contenant t, s1, s2 pour le premier et t, s1, s5 pour le second, ne sont pas coplanaires.
- Tout point de S contient au moins 5 arêtes de longueur d dans le polyèdre. En effet, si v est un sommet quelconque de S, il existe une rotation de G qui envoie t sur v, car S est défini comme l'orbite de t. Cette rotation envoie s1 sur un point de S à une distance de d de v, le groupe des rotations de G laissant v invariant montre l'existence de 5 images par les éléments du groupe à situés à une distance d de v. Le caractère isométrique de la rotation montre que ce sont les seuls points de S à une distance inférieure ou égale à d de v.
Ce raisonnement montre l'existence de 30 arêtes dans le polyèdre, chaque point contient en effet 5 arêtes de longueur d, il existe 12 points dans S et chaque arrête contient 2 sommets, ce qui donne 12x5/2, soit 30 arêtes. Cependant rien ne garantit encore que ce sont les seules arêtes de P, on ne sait pas si [s1, s2] est de longueur d et si c'est une arête de P. Pour élucider cette question, étudions les faces du polyèdre.
-
-
- Structure des faces du polyèdre :
-
- Considérons les triangles de type t, s1, s2, c'est-à-dire formé par un point de S, un deuxième à distance d du premier et pour troisième l'image par une rotation d'axe t et d'angle un cinquième de tour. Comme la rotation est élément de G, s2 est bien un sommet de P. L'objectif est de montrer que ces triangles sont équilatéraux et forment les faces du polyèdre. Montrons qu'ils recouvrent le polyèdre, ou encore que tout point p de P est à une distance inférieure à d d'un sommet. Soit t le point le plus proche de p, s1, ..., s5 les 5 points de S à une distance d de t et C le cercle contenant ces 5 points. Les points à l'extérieur de la calotte sphérique de la sphère contenant S, délimité par le cercle C et contenant t, sont tous plus proches d'un des cinq points s1, ..., s5 que de t. On en déduit que p est dans la calotte, ce qui montre qu'il est dans un des triangles considérés.
- Soit ψ une rotation d'un tiers de tour de G. Son axe croise le polyèdre et donc un des triangles précédents, noté ici T. L'intersection c de l'axe et du triangle n'est pas un sommet du polyèdre car les sommets ont un stabilisateur d'ordre 5, qui ne contient aucun élément d'ordre 3. Soit s1 le point de S le plus proche de c. Les images de s1 par les rotations ψ et ψ2 sont deux points de S tout aussi proche de c que l'est s1. On en déduit que ces trois points sont les sommets de T, ce montre que T est équilatéral. Tout triangle de la famille précédente est isomorphe à T. En effet, soit T1 un des triangles, une isométrie transporte un des sommets de T1 sur l'un des sommets t de T, puis l'une des 5 rotations d'axe dirigé par t fait coïncider le triangle image avec T.
La structure du polyèdre est maintenant totalement élucidée. Si t est un sommet de S et s1, ..., s5 les 5 points de S à une distance d de t, [s1, s2] est bien une arête du polyèdre car sa longueur est égale à d. Les points s2, t s5 sont sur la même orbite pour le stabilisateur de s1 et l'on a démontré que les segments d'extrémités s1 et l'un des points de l'orbite, est une arête. On remarque qu'un sommet est partagé par 5 faces et que chaque face est partagé par 3 sommets, ce qui montre l'existence de 12x5/3 = 20 faces. Le polyèdre construit est bien un solide de Platon car il est régulier, on reconnaît d'ailleurs l'icosaèdre.
-
-
- Construction du dodécaèdre :
-
- Le dodécaèdre est le polyèdre dual de l'icosaèdre. Il est régulier et possède le même groupe de rotation G, comme tous les polyèdres duaux d'un polyèdre régulier. Ces sommets sont les centres des faces de l'icosaèdre, comme l'icosaèdre contient 20 faces, il possède 20 sommets. Le centre de chacune des faces se situe sur l'axe contenant le vecteur nul et un sommet de l'icosaèdre. Cet axe est celui d'une rotation d'ordre 5 de G, ce qui montre que chaque face est un pentagone dont le plan est orthogonal à l'axe de la rotation. De plus il existe autant de faces que l'icosaèdre contient de sommets, c'est-à-dire 12. Le dodécaèdre contient 20 sommets chacun centre d'une rotation d'ordre 3, chaque sommet contient donc 3 arêtes. Il existe 12 sommets, donc 20x3/2 = 30 arêtes.
Notes et références
Notes
- C'est par exemple la définition donnée dans Groupe alterné par Bibmath
- C'est par exemple le choix de : N. Lanchier Groupe des permutations d’un ensemble fini. Applications. de l'Université de Rouen
- C'est le choix par exemple de M. Hindry Liste des groupes simples finis de L'Université de Jussieu Paris VII
- Groupe des permutations d'un ensemble fini IUFM de la Réunion
- Cette définition est utilisée dans : A. et R. Douady Algèbre et théories galoisiennes Cassini 2005 (ISBN 2842250052) p 318
- cité par Edouard Lucas, dans Récréations mathématiques (1891), réédition Librairie Blanchard (1992) p 190 (ISBN 2853671232)
- La démonstration proposée ici provient de M. Coste Jeu de taquin et générateurs du groupe alterné Université de Rennes 1 (2008)
- W. R. Scott Group Theory Dover Publications (1987) p 299 (ISBN 0486653773)
- Une démonstration est proposé par : R. Bédard Caractère du groupe alterné Université du Québec à Montréal 2007 p76
- La démonstration proposée provient de : A. et R. Douady Algèbre et théories galoisiennes Cassini 2005 p 319 (ISBN 2842250052)
- On trouve une démonstration dans : M. Hindry Cours d'algèbre au magistère de Cachan Université Paris VII p 22. Voir aussi J.S. Rose, A Course on Group Theory, Cambridge 1978, réimpr. Dover, 1994, théor. 5.30, p. 106. Soit G un groupe simple d'ordre 60. L'essentiel de la démonstration consiste à montrer, en considérant l'opération de G sur ses 2-sous-groupes de Sylow, que G est isomorphe à un sous-groupe de S_{5}.
- La démonstration proposée provient de : A. et R. Douady Algèbre et théories galoisiennes Cassini 2005 p 320 (ISBN 2842250052)
- M. Hindry Cours d'algèbre au magistère de Cachan Université Paris VII p 22
- Cet exemple provient de : A. et R. Douady Algèbre et théories galoisiennes Cassini 2005 p 322 (ISBN 2842250052)
- On peut vérifier par exemple sur : R. Bédard Représentations des groupes Université du Québec à Montréal p 29
- Une démonstration est proposé par : R. Bédard Caractère du groupe alterné Université du Québec à Montréal 2007 p78
- Cette démonstration s'inspire de : R. Bédard Caractère du groupe alterné Université du Québec à Montréal 2007 p 78
Liens externes
- M. Coste, Jeu de taquin et générateurs du groupe alterné Université de Rennes 1 (2008)
- V. & F. Bayard, Groupe alterné Bibmath
Bibliographie
- Daniel Perrin, Cours d'algèbre [détail des éditions]
- (en) W. R. Scott, Group Theory Dover Publications (1987) p. 299 (ISBN 0486653773)
- A. et R. Douady, Algèbre et théories galoisiennes Cassini 2005 (ISBN 2842250052)
- Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
- M. J. Wenninger, Dual Models Cambridge University Press 1983 (ISBN 0521245249)
-
Wikimedia Foundation. 2010.