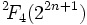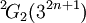Groupe de type de lie

Groupe de type de Lie

En mathématiques, un groupe de type de Lie G(k) est un groupe (non nécessairement fini) de points rationnels d'un groupe algébrique linéaire G à valeur dans le corps k. La classification des groupes simples finis montre que les groupes de types de Lie finis incluent tous les groupes finis simples autres que les groupes cycliques, les groupes alternés, le groupe de Tits et les 26 groupes sporadiques simples. Les cas particuliers incluent les groupes classiques, les groupes de Chevalley, les groupes de Steinberg et les groupes de Suzuki-Ree.

Les groupes classiques

Article détaillé : Groupe classique.

Une approche initiale est la définition et l'étude détaillée de ce que l'on appelle les groupes classiques sur des corps finis et autres. Beaucoup de travaux ont été réalisés la-dessus, à partir de l'époque de L. E. Dickson jusqu'à l'ouvrage de Jean Dieudonné. Par exemple, Emil Artin a étudié les ordres de tels groupes, en vue de classifier les cas de coïncidence.

Un groupe classique est, de manière grossière, un groupe spécial linéaire, orthogonal, symplectique ou unitaire. Il existe plusieurs variations mineures de ceux-ci, données en prenant les sous-groupes dérivés ou par quotient avec le centre. Ils peuvent être construits sur les corps finis (ou tout autre corps) plus ou moins de la même façon qu'ils ont été construits sur les nombres réels. Ils correspondent aux séries :

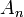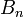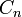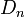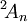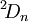$A_n\,$ , $B_n\,$ , $C_n\,$ , $D_n\,$ , ${}^2\!A_n\,$ , ${}^2\!D_n\,$ des groupes de Chevalley et Steinberg.

Les groupes de Chevalley

La théorie a été clarifiée par la théorie des groupes algébriques et par le travail de Claude Chevalley, dans le milieu des années 50, sur les algèbres de Lie au moyen duquel le concept de groupe de Chevalley a été isolé. Chevalley a construit une base de Chevalley (une sorte de forme intégrale) pour toutes les algèbres de Lie simples complexes (ou plutôt de leurs algèbres enveloppantes universelles), qui peuvent être utilisées pour définir les groupes algébriques correspondants sur les entiers. En particulier, il a pu prendre leurs points à valeurs dans tout corps fini. Pour les algèbres de Lie 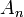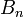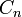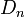$A_n\,$ , $B_n\,$ , $C_n\,$ , $D_n\,$ ceci donnait les groupes classiques bien connus, mais sa construction donna aussi les groupes associés aux algèbres de Lie exceptionnelles

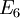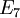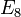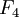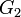$E_6\,$ , $E_7\,$ , $E_8\,$ , $F_4\,$ et $G_2\,$ . (Certains de ceux-ci avaient déjà été construits par Dickson.)

Les groupes de Steinberg

La construction de Chevalley ne donnait pas tous les groupes classiques connus : elle omettait les groupes unitaires et les groupes orthogonaux non séparés. Steinberg trouva une modification de la construction de Chevalley qui donne ces groupes et quelques nouvelles familles. Sa construction est similaire à la construction habituelle du groupe unitaire à partir du groupe linéaire général. Le groupe linéaire général sur les nombres complexes possède un "automorphisme de diagramme" donné en prenant la transposée inverse et un "automorphisme de corps" donné en prenant la conjugaison complexe. Le groupe unitaire est le groupe des point fixés du produit de ces deux automorphismes. De la même manière, beaucoup de groupes de Chevalley ont des "automorphismes de diagramme" induits par les automorphismes de leurs diagrammes de Dynkin et des "automorphismes de corps" induits par les automorphismes d'un corps fini. Steinberg a construit des familles de groupes en prenant des points fixés d'un produit d'un diagramme et d'un automorphisme de corps. Ceux-ci donnèrent les groupes unitaires :

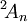${}^2\!A_n\,$ provenant de l'automorphisme d'ordre 2 de 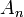$A_n\,$ , certains groupes orthogonaux supplémentaires 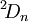${}^2\!D_n\,$ de l'automorphisme d'ordre 2 de 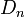$D_n\,$ et deux nouvelles séries de ${}^2\!E_6\,$ ,

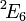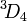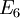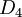${}^3\!D_4\,$ des automorphismes d'ordre 2 et 3 de $E_6\,$ et de $D_4\,$ . (Les groupes de types 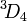${}^3\!D_4\,$ n'ont pas d'analogue sur les réels, comme les nombres complexes n'ont pas d'automorphisme d'ordre 3).

Les groupes de Suzuki-Ree

Autour de 1960, Suzuki fit sensation en découvrant une nouvelle série infinie de groupes qui semblait, de prime abord, non relié aux groupes algébriques connus. Ree sut que le groupe algébrique 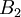$B_2\,$ possédait un automorphisme "supplémentaire" de caractéristique 2 dont le carré était l'automorphisme de Frobenius. Il trouva que si un corps fini de caractéristique 2 possède aussi un automorphisme dont le carré est l'application de Frobenius, alors un analogue de la construction de Steinberg donne les groupes de Suzuki. Les corps avec un tel automorphisme sont ceux d'ordre 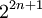$2^{2n+1}\,$ , et les groupes correspondants sont les groupes de Suzuki

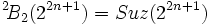${}^2\!B_2(2^{2n+1}) = Suz(2^{2n+1})\,$ .

(à strictement parler, le groupe Suz(2) n'est pas compté comme un groupe de Suzuki comme il n'est pas simple : c'est le groupe de Frobenius d'ordre 20). Ree a pu trouver deux nouvelles familles similaires

${}^2\!F_4(2^{2n+1})\,$

${}^2\!G_2(3^{2n+1})\,$

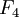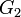de groupes simples en utilisant le fait que $F_4\,$ et $G_2\,$ ont des automorphismes supplémentaires de caractéristiques 2 et 3. (En parlant grossièrement, en caractéristique p, il est permis d'ignorer la flèche sur les liens de multiplicité p dans le diagramme de Dynkin en prenant les automorphismes de diagramme). Le plus petit groupe 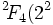${}^2\!F_4(2^{2}\,$ de type 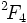${}^2\!F_4\,$ est non simple, mais il possède un sous-groupe simple d'index 2, appelé le groupe de Tits (nommé en l'honneur du mathématicien belge Jacques Tits). Le plus petit groupe 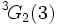${}^3\!G_2(3)\,$ de type 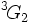${}^3\!G_2\,$ est non simple, mais il possède un sous-groupe normal d'index 3, isomorphe à 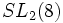$SL_2(8)\,$ . Dans la classification des groupes simples finis, les groupes de Ree

${}^2\!G_2(3^{2n+1})\,$

sont ceux dont la structure est la plus difficile à "dégoupiller" explicitement. Ces groupes ont aussi joué un rôle dans la découverte du premier groupe sporadique moderne. Ils ont des centralisateurs d'involution de la forme Z/2Z × PSL₂(q) pour q = 3ⁿ, et en étudiant les groupes avec un centralisateur d'involution de forme similaire Z/2Z × PSL₂(5) Janko découvrit le groupe sporadique .

Les petits groupes de type de Lie

Beaucoup des plus petits groupes dans les familles ci-dessus ont des propriétés spéciales non partagées par la plupart des membres de la famille.

Quelquefois les plus petits groupes sont résolubles plutôt que simples; par exemple les groupes SL₂(2) et SL₂(3) sont résolubles.

Il existe un nombre ahurissant d'isomorphismes "accidentels" entre divers petits groupes de type de Lie (et les groupes alternés). Par exemple, les groupes SL₂(4), PSL₂(5) et le groupe alterné sur 5 points sont tous isomorphes.

Certains des petits groupes ont un multiplicateur de Schur qui est plus grand que prévu. Par exemple, les groupes A_n(q) ont habituellement un multiplicateur de Schur d'ordre (n + 1, q - 1), mais le groupe A₂(4) possède un multiplicateur de Schur d'ordre 48, à la place de la valeur prévue 3.

Pour une liste complète de ces exceptions, voir la liste des groupes simples finis. Beaucoup de ces propriétés spéciales sont reliées à certains groupes sporadiques simples. L'existence de ces petits phénomènes n'est pas entièrement une question 'triviale'; ils sont réfléchis ailleurs, par exemple dans la théorie de l'homotopie.

Les groupes alternés se comportent quelquefois comme s'ils étaient des groupes de types de Lie sur le corps (non-existant) à 1 élément. Certains des petits groupes alternés ont aussi des propriétés exceptionnelles. Les groupes alternés ont habituellement un groupe d'automorphisme extérieur d'ordre 2, mais le groupe alterné sur 6 points possède un groupe d'automorphisme extérieur d'ordre 4. Les groupes alternés ont un multiplicateur de Schur d'ordre 2, mais ceux sur 6 ou 7 points ont un multiplicateur de Schur d'ordre 6.

Questions de notations

Malheureusement, il n'existe pas de notation standard pour les groupes de type de Lie finis, et la littérature contient des douzaines de systèmes de notations incompatibles et confus.

Les groupes de type 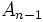$A_{n-1}\,$ sont quelquefois notés par 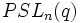$PSL_n(q)\,$ (le groupe projectif linéaire spécial) ou par $L_n(q)\,$ .

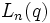Les groupes de type 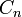$C_n\,$ sont quelquefois notés par 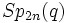$Sp_{2n}(q)\,$ (le groupe symplectique) ou par 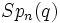$Sp_n(q)\,$ (dans le cas d'auteurs à l'esprit particulièrement diabolique).

La notation pour les groupes orthogonaux est particulièrement confuse. Certains symboles utilisés sont 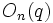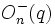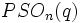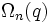$O_n(q)\,$ , $O^{-}_n(q)\,$ , $PSO_n(q)\,$ , $\Omega_n(q)\,$ , mais il existe tellement de conventions qu'il n'est pas possible de dire exactement quels groupes y correspondent. Certains auteurs utilisent un piège particulièrement vicieux : 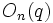$O_n(q)\,$ pour un groupe qui n'est pas le groupe orthogonal, mais le groupe simple correspondant.

Pour les groupes de Steinberg, certains auteurs écrivent 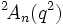${}^2\!A_n(q^2)\,$ (et ainsi de suite) pour le groupe que d'autres auteurs désignent par 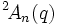${}^2\!A_n(q)\,$ . Le problème est qu'il existe deux corps impliqués, un d'ordre 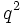$q^2\,$ et son corps fixé d'ordre q et les lecteurs ont des idées différentes sur celui qui devrait être inclus dans la notation. La convention " 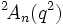${}^2\!A_n(q^2)\,$ " est plus logique et conforme, mais la convention " 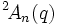${}^2\!A_n(q)\,$ " est de loin la plus commune.

Les auteurs diffèrent si des groupes tels que 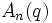$A_n(q)\,$ sont les groupes de points à valeurs dans le groupe simple ou le groupe algébrique simplement connecté. Par exemple, 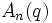$A_n(q)\,$ peut signifier soit le groupe spécial linéaire 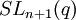$SL_{n+1}(q)\,$ ou le groupe projectif spécial linéaire 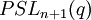$PSL_{n+1}(q)\,$ . Donc 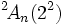${}^2\!A_n(2^2)\,$ peut être un des 4 groupes différents, dépendant de l'auteur.

Lectures avancées

Une référence standard :

Simple Groups of Lie Type par Roger W. Carter, ISBN 0-471-50683-4

Les groupes classiques sont décrits dans

La géométrie des groupes classiques par Jean Dieudonné

Portail des mathématiques

Ce document provient de « Groupe de type de Lie ».

Catégorie : Groupe remarquable

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe de type de lie de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Groupe De Type De Lie — En mathématiques, un groupe de type de Lie G(k) est un groupe (non nécessairement fini) de points rationnels d un groupe algébrique linéaire G à valeur dans le corps k. La classification des groupes simples finis montre que les groupes de types… … Wikipédia en Français
Groupe de type de Lie — En mathématiques, un groupe de type de Lie G(k) est un groupe (non nécessairement fini) de points rationnels d un groupe algébrique linéaire réductif (en) G à valeur dans le corps commutatif k. La classification des groupes simples finis… … Wikipédia en Français
Groupe De Tits — En mathématiques, le groupe de Tits est un groupe simple fini d ordre 17 971 200 nommé en l honneur du mathématicien français Jacques Tits. C est le sous groupe dérivé du groupe de Chevalley tordu . À strictement parler, le groupe de… … Wikipédia en Français
Groupe de tits — En mathématiques, le groupe de Tits est un groupe simple fini d ordre 17 971 200 nommé en l honneur du mathématicien français Jacques Tits. C est le sous groupe dérivé du groupe de Chevalley tordu . À strictement parler, le groupe de… … Wikipédia en Français
Groupe de Tits — En mathématiques, le groupe de Tits est un groupe simple fini d ordre 17 971 200 = 211 · 33 · 52 · 13 nommé en l honneur du mathématicien Jacques Tits. C est le sous groupe dérivé du groupe Ree .… … Wikipédia en Français
Groupe sanguin — Pour le groupe humoristique québécois, voir Le Groupe sanguin. Un groupe sanguin est une classification de sang reposant sur la présence ou l absence de substance antigéniques héritées à la surface des globules rouges (hématies). Ces antigènes… … Wikipédia en Français
Groupe de recherche et d'études sur la civilisation européenne — Groupement de recherche et d études pour la civilisation européenne Ne doit pas être confondu avec Grèce ou Nouvelle droite française. Groupement de recherche et d études pour la civilisation européenne … Wikipédia en Français
Groupe (mathématique) — Groupe (mathématiques) Pour les articles homonymes, voir Groupe. Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes … Wikipédia en Français
Groupe Algébrique — En géométrie algébrique, la notion de groupe algébrique est un équivalent des groupes de Lie en géométrie différentielle ou complexe. Un groupe algébrique est une variété algébrique munie d une loi de groupe compatible avec sa structure de… … Wikipédia en Français
Groupe algebrique — Groupe algébrique En géométrie algébrique, la notion de groupe algébrique est un équivalent des groupes de Lie en géométrie différentielle ou complexe. Un groupe algébrique est une variété algébrique munie d une loi de groupe compatible avec sa… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Groupe de type de lie