Classe de conjugaison

En mathématiques, dans la théorie des groupes, une action par conjugaison est un cas particulier d'action de groupe. L'ensemble X sur lequel agit le groupe G est ici le groupe G lui-même.

Dans cet article :

(G, * ) désigne un groupe, noté multiplicativement, de neutre e.

La loi * du groupe est le plus souvent sous-entendue.

Sommaire 1 Définitions 2 Applications 3 Exemples 4 Propriétés 5 Voir aussi

Définitions

• Soit g un élément de G, l'application aut_g de G dans G, qui à x associe gxg^-1 est appelée automorphisme intérieur associé à g :

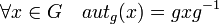
Cette application est bien bijective car elle est composée de deux bijections, une translation à droite et une translation à gauche ; on vérifie le fait qu'elle est bien un morphisme :

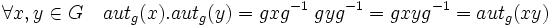
On définit une nouvelle loi interne par :

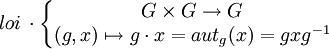
• Cette loi interne de G constitue une action de groupe, appelée action de conjugaison.

Démonstration : on vérifie les deux conditions d'une action de groupe.

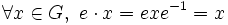car e est le neutre de G

 :

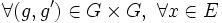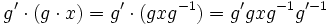
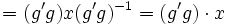
• Pour tout g appartenant à G, la classe de g par l'action par conjugaison est appelée classe de conjugaison de g et est notée C_j(g) :

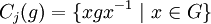
Tout élément de C_j(g) est appelé conjugué de g.

Applications

• Les classes de conjugaison sont utilisées pour la démonstration du théorème de Wedderburn stipulant que tout corps fini est commutatif.
• Dans le cadre de la théorie des représentations d'un groupe fini, les classes de conjugaison sont à la base de la définition des fonctions centrales d'un groupe fini, elles servent à définir l'espace vectoriel, les caractères des représentations. Dans le même contexte, on les retrouve pour l'analyse du centre d'une algèbre d'un groupe.
• Les automorphismes intérieurs sont utilisés pour la démonstration des théorèmes de Sylow, du théorème de Frattini et dans de nombreuses démonstrations concernant les groupes.
• La diagonalisation de matrices consiste à trouver une bonne action par conjugaison égale à une matrice donnée.
• La conjugaison d'un quaternion purement imaginaire par un quaternion unitaire équivaut à la rotation d'un vecteur de l'espace à trois dimensions. La conjugaison d'un quaternion purement imaginaire par un quaternion quelconque équivaut à une similitude.

Exemples

• Les classes de conjugaison d'un groupe symétrique sont composées de produits de cycles à supports disjoints de même structure. Ceci signifie que le nombre de cycles de même longueur est le même pour chaque élément d'une classe de conjugaison.
• Les classes de conjugaison d'un groupe alterné et du groupe simple d'ordre 168 sont étudiées dans l'article associé.

Propriétés

• Les classes de conjugaison constituent une partition de G associée à la relation d'équivalence : .

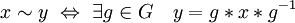• Un élément g de G laisse invariant tout élément de G si et seulement si g appartient au centre Z(G) de G :

.

On peut donc restreindre l'action par conjugaison au groupe quotient G/Z(G). Alors f_g = f_g' ssi g = g' mod[Z(G)], où f_g est l'automorphisme intérieur défini par .

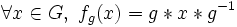• De même z opère identiquement sur x (l'action par conjugaison de z stabilise x) si et seulement si z est élément du centralisateur Z_x de x. La formule des classes montre alors que, si C_x désigne la classe de congugaison de x :

.

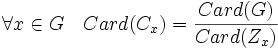Remarque : La formule précédente montre en particulier que le cardinal de toute classe de conjugaison divise le cardinal de G.

Voir aussi

• Action de groupe
• Centralisateur
• Sous-groupe normal

• Portail des mathématiques