Relation d'ordre

Une relation d’ordre dans un ensemble est une relation binaire dans cet ensemble qui permet de comparer ses éléments entre eux de manière cohérente. Un ensemble muni d’une relation d’ordre est un ensemble ordonné ou tout simplement un ordre.

Sommaire 1 Définitions et exemples 1.1 Relation d'ordre 1.2 Ensemble ordonné 1.3 Exemples et contre-exemples 2 Notions associées 2.1 Applications croissantes 2.2 Plus grand élément et élément maximal 2.3 Relation d'ordre strict 2.4 Négation (ou complémentaire) d'une relation d'ordre 2.5 Ordre dual 2.6 Préordre 3 Propriétés complémentaires 3.1 Compatibilité 3.2 Ensemble bien ordonné 3.3 Treillis 4 Applications 4.1 Topologie de l'ordre 4.2 Liens avec les complexes simpliciaux 5 Références 6 Voir aussi

Définitions et exemples

Relation d'ordre

Une relation d'ordre est une relation binaire réflexive, transitive et antisymétrique : soit E un ensemble et une relation binaire sur cet ensemble notée « ≤ », cette relation est une relation d'ordre si pour tous x, y et z éléments de E :

• x ≤ x (réflexivité)
• (x ≤ y et y ≤ x) ⇒ x = y (antisymétrie)
• (x ≤ y et y ≤ z) ⇒ x ≤ z (transitivité)

De par la forme même de ces axiomes, ceux-ci sont vérifiés par la relation binaire ≥, qui est définie par

x ≥ y si et seulement si y ≤ x.

À toute relation d'ordre est donc associée une relation d'ordre réciproque sur le même ensemble (plus petit ou égal / plus grand ou égal, inférieur ou égal / supérieur ou égal etc.). On associe également à toute relation d'ordre ≤, une relation dite d’ordre strict notée alors < (qui n'est pas à proprement parlé une relation d'ordre puisque la réflexivité n'est pas satisfaite), qui est la restriction de la relation d'ordre aux couples d'éléments distincts :

x < y si et seulement si x ≤ y et x ≠ y.

Une relation d'ordre au sens de la définition ci-dessus est parfois qualifiée d’ordre large.

Pour certaines relations d'ordre, deux éléments de E sont toujours comparables, c'est-à-dire que pour tous x, y de E :

x ≤ y ou y ≤ x.

On dit alors que la relation d'ordre est totale, et que l'ensemble E est totalement ordonné par cette relation. Une relation d'ordre sur E est dite partielle si elle n'est pas totale, et E est alors partiellement ordonné. Il est à noter qu'en anglais, on désigne par ordre partiel un ordre quelconque, qui peut donc être total. Cette terminologie est parfois également utilisée en français.

Ensemble ordonné

Un ensemble ordonné est un ensemble muni d'une relation d'ordre. Si un ensemble ordonné est fini, il peut être représenté graphiquement sous la forme d'un diagramme de Hasse, de façon similaire à la représentation habituelle d’un graphe sur papier, ce qui peut permettre de travailler plus aisément dessus. Si il est infini, on peut dessiner une partie de son diagramme de Hasse.

Exemples et contre-exemples

• La relation « est inférieur ou égal à » est une relation d'ordre total sur l'ensemble des entiers (naturels ou relatifs), sur l'ensemble des rationnels ou l'ensemble des réels.

• La relation « est strictement inférieur à », par exemple sur l'ensemble des entiers naturels, n'est pas une relation d'ordre car elle n'est pas réflexive (une relation d'ordre strict n'est jamais un ordre large).

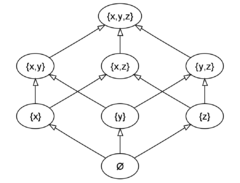
• La relation d'inclusion, « est un sous-ensemble de » ou « est contenu dans » est une relation d'ordre partiel sur l'ensemble des parties d'un ensemble. Si l'ensemble donné est fini, son ensemble des parties est fini (plus précisément pour , on a ). La figure ci-dessous représente le diagramme de Hasse d'un ensemble à 3 éléments.

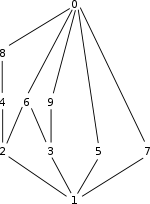
• La relation de divisibilité est une relation d'ordre partiel sur les entiers naturels, mais ce n'est pas une relation d'ordre sur les entiers relatifs car elle n'est pas antisymétrique : 1 divise -1 et -1 divise 1. La figure ci-dessous représente le diagramme de Hasse de la relation de divisibilité entre les entiers de 0 à 9.

• L'ensemble des fonctions de dans , muni de la relation d'ordre f < g si , est un ensemble ordonné infini. Intuitivement, une fonction est plus petite qu'une autre si sa courbe est toujours en dessous de l'autre courbe. On peut généraliser cet exemple aux fonctions d'un ensemble X dans un ensemble ordonné P.

• L'ensemble des partitions d'un ensemble donné est partiellement ordonné, avec la relation d'ordre donnée par le raffinement des partitions : par définition, une partition est plus fine qu'une autre si elle fractionne les parties de l'autre en de plus petites parties.

• Étant donnés deux ensembles ordonnés E et F, il y a au moins deux façons naturelles de définir un ordre sur .
  • L'ordre produit : (x, y) ≤ (x’, y’) si et seulement si x ≤ x’ et y ≤ y’.
  • L'ordre lexicographique : (x, y) ≤ (x’, y’) si et seulement si [x < x’ ou [x = x’ et y ≤ y’]].

Si les ordres initiaux sont totaux, l'ordre lexicographique est aussi total (mais pas en général l'ordre produit). Par exemple la relation ≤ définie sur l'ensemble des complexes par

  si et seulement si   ou et

est une relation d'ordre total. Elle n'est cependant pas compatible avec la structure de corps de l'ensemble des complexes.

• On peut munir R[X₁,...,X_n] l'ensemble des polynômes à n variables d'une relation d'ordre partielle. On commence par comparer les monômes à n variables via l'ordre lexicographique induit par 1 < X₁ < X₂ < ... < X_n (cet ordre lexicographique est total). On compare deux polynômes P et Q en disant que P est strictement plus petit que Q si tout monôme non nul de P est strictement plus petit que tout monôme non nul de Q. Cette relation d'ordre sur les polynômes est partielle.

• On ne peut définir de façon satisfaisante une relation d'ordre sur le cercle qui signifierait « est placé avant ». Par exemple, sur l'ensemble des points du cercle trigonométrique (de centre O), la relation entre deux points M et N définie par « la mesure principale de l'angle ([OM),[ON)) » est positive ou nulle n'est pas une relation d'ordre car elle n'est pas transitive.
• La relation « est le père de » sur un ensemble de personnes n'est pas une relation d'ordre car elle n'est pas transitive.

Notions associées

Applications croissantes

Si (E, ≤_E) et (F, ≤_F) sont deux ensembles ordonnés, une application f de E dans F est dite croissante (ou parfois croissante au sens large) quand elle conserve l'ordre, décroissante (au sens large) quand elle inverse celui-ci, c'est-à-dire que :

f est croissante quand pour tous x et y de E,   x ≤_E y ⇒ f(x) ≤_F f(y).

f est décroissante quand pour tous x et y de E pour tous x et y de E,   x ≤_E y ⇒ f(x) ≥_F f(y).

Quand elle conserve l'ordre strict elle est strictement croissante : pour tous x et y de E,   x <_E y ⇒ f(x) <_F f(y),

et strictement décroissante quand elle l'inverse : pour tous x et y de E,   x <_E y ⇒ f(x) >_F f(y).

À noter qu'une application injective croissante est nécessairement strictement croissante.

Les morphismes d'ordres sont les applications croissantes.

Une application monotone ou monotone au sens large (resp. strictement monotone) est une application croissante ou décroissante (resp. strictement croissante ou strictement décroissante).

Plus grand élément et élément maximal

Dans un ensemble ordonné E, il n'existe pas forcément de plus grand élément. Si E est fini, il contiendra (au moins) un élément maximal. Si E est un ensemble inductif infini, le lemme de Zorn garantit encore l'existence d'un élément maximal.

Relation d'ordre strict

On a vu qu'à une relation d'ordre « ≤ » sur un ensemble donné, on associait naturellement une relation « < », dite d’ordre strict, définie sur le même ensemble, et obtenue en restreignant celle-ci aux couples d'éléments distincts. Il est tout à fait possible d'axiomatiser directement la notion d'ordre strict. Cela peut même s'avérer plus naturel dans certains cas.

Une relation d'ordre strict est une relation binaire irréflexive, et transitive : soit E un ensemble et une relation binaire sur cet ensemble notée <, cette relation est une relation d'ordre strict si et seulement si pour tous x, y et z éléments de E :

• non (x < x) (irréflexivité)
• (x < y et y < z) ⇒ x < z (transitivité)

On déduit immédiatement de ces deux propriétés qu'une relation d'ordre strict est antisymétrique. À dire vrai une relation d'ordre strict est antisymétrique en un sens plus fort qu'une relation d'ordre large, c’est-à-dire que pour tous x et y de l'ensemble support E :

• x < y ⇒ non (y < x) (antisymétrie « forte »)

Cependant pour une relation irréflexive, comme les ordres stricts, cette propriété est équivalente à la propriété d'antisymétrie définie pour les ordres larges. Il n'y a donc pas d'inconvénient à parler d'antisymétrie dans les deux cas.

De même qu'à une relation d'ordre (large) on associait une relation d'ordre strict, à une relation d'ordre strict, soit « < », on associe naturellement une relation d'ordre large, soit « ≤ », définie par :

x ≤ y si et seulement si x < y ou x = y.

Choisir l'une ou l'autre des axiomatisations n'a pas d'importance en soi. Dans les deux cas on a défini un ordre large et un ordre strict associés. En effet on vérifie facilement, en utilisant les propriétés de l'égalité, que :

• La relation d'ordre strict associée à une relation d'ordre large (transitive, réflexive et antisymétrique) vérifie bien les axiomes d'ordre stricts (elle est transitive et irréflexive).
• La relation d'ordre large associée à une relation d'ordre strict (transitive et irréflexive) vérifie bien les axiomes d'ordre large (elle est transitive, réflexive et antisymétrique).
• Il y a bien symétrie : étant données une relation d'ordre strict « < », et une relation d'ordre large « ≤ », « < » est associée à « ≤ » si et seulement si « ≤ » est associée à « < ».

Pour un ordre strict, la totalité s'exprime ainsi :

∀ x, y ∈ E ( x < y ou x = y ou y < x ).

et on dit alors que c'est une relation d'ordre strict total. Il n'y a pas de confusion possible avec le sens précédent de relation totale, car une relation d'ordre strict, qui est irréflexive, ne peut être totale au sens où l'est un ordre large.

Pour un ordre strict total, les trois possibilités — x < y, x = y et y < x — sont exclusives, et l'on parle parfois, à la suite de Cantor, de propriété de trichotomie.

Négation (ou complémentaire) d'une relation d'ordre

La négation d'une relation binaire R définie sur un ensemble A est la relation de graphe le complémentaire de celui de R dans . On la note . Dit autrement, deux éléments sont en relation par si et seulement s'ils ne le sont pas par R.

Dire qu'un ordre est total, c'est dire que sa négation est l'ordre strict inverse. C’est-à-dire qu'il y a équivalence pour un ordre entre :

• est total ;
• 

Par contre dès qu'il existe deux éléments distincts non comparables par un ordre, sa négation ne peut être un ordre (strict ou large), car elle n'est pas antisymétrique. La négation d'un ordre non total n'est donc jamais un ordre.

Par exemple, la négation de l'inclusion ⊄ sur l'ensemble des parties d'un ensemble d'au moins deux éléments n'est pas un ordre, car, si a ≠ b, on a toujours {a}≠{b} avec cependant {a}⊄{b} et {b}⊄{a}.

Ordre dual

Le dual d'un ensemble ordonné P=(E, ≤) est l'ensemble ordonné P^op=(E, ≥) : si ≤ est une relation d'ordre sur E, alors la relation ≥ sur E définie par

en est une également.

Préordre

Un préordre est une relation binaire réflexive et transitive.

On peut le considérer comme une relation d’ordre dans laquelle on autoriserait les cycles non triviaux (c’est-à-dire des cycles de plus d’un élément). Ajouter la condition d'anti-symétrie rend impossible la présence de ces cycles non triviaux.

Tout quotient d'un préordre par la relation d'équivalence associée est un ordre.

Propriétés complémentaires

Compatibilité

Une relation d’ordre sur un ensemble E muni d’une loi de composition interne * est compatible avec cette loi si et seulement si :

• La relation d'ordre sur l'ensemble des réels est compatible avec l'addition mais pas avec la multiplication.
• La relation d'ordre sur l'ensemble des réels strictement positifs est compatible avec l'addition et la multiplication.
• L’ensemble des nombres complexes n’est pas ordonnable par une relation d’ordre compatible avec les opérations d’addition et de multiplication.

Si un groupe est muni d'une relation d'ordre compatible avec sa loi interne, on l'appelle groupe ordonné.

Un groupe totalement ordonné vérifiant la propriété

est dit archimédien.

Ensemble bien ordonné

Un ensemble ordonné est dit bien ordonné si tout sous-ensemble non vide de cet ensemble possède un plus petit élément.

Treillis

Un ensemble est appelé treillis s'il est ordonné et que tout couple d'éléments possède une borne supérieure et une borne inférieure. Une borne supérieure (resp. inférieure) étant un élément plus grand (resp. plus petit) que chacun des éléments de la paire et tel que tout autre élément ayant la même propriété est plus grand (resp. plus petit) que la borne. Autrement dit, une borne est le plus petit majorateur (resp. le plus grand minorateur). Si on représente le treillis par un graphe orienté, cela revient à dire que toute paire de nœuds a un ancêtre et un descendant communs.

Applications

Topologie de l'ordre

Un ensemble ordonné peut être muni de plusieurs topologie issues de l'ordre : la topologie de l'ordre, la topologie de l'ordre à droite et la topologie de l'ordre à gauche.

Liens avec les complexes simpliciaux

Une classe importante de complexes simpliciaux provient d'ensembles ordonnés finis. On définit le complexe d'ordre D(P) d'un ensemble ordonné fini P comme étant l'ensemble des chaînes de P. Le complexe d'ordre est trivialement un complexe simplicial.

L'étude de l'ensemble ordonné en lui-même donne des informations sur son complexe d'ordre, et il est donc intéressant d'étudier un complexe simplicial comme le complexe d'ordre d'un ensemble ordonné.

Références

Richard P. Stanley, Enumerative Combinatorics, vol.1, Cambridge Studies in Advanced Mathematics 49, Cambridge University Press, ISBN 0-521-66351-2

Voir aussi

• Ordre partiel complet
• Corps ordonné
• Antichaîne

• Portail des mathématiques