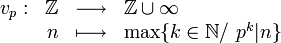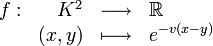- Valuation p-adique
-
Valuation
En mathématiques, plus particulièrement en géométrie algébrique et en théorie des nombres, une valuation est une mesure de la multiplicité. La notion est une généralisation de la notion de degré ou d'ordre d'annulation d'un polynôme formel en algèbre, du degré de divisibilité par un nombre premier en théorie des nombres, de l'ordre d'un pôle en analyse complexe ou du nombre de points de contact entre deux variétés algébriques en géométrie algébrique.
Il existe une définition particulière pour les polynômes : la valuation d'un polynôme est le degré de son monôme de plus petit degré si le polynôme est non nul et plus l'infini sinon (cf l'article Construction de l'anneau des polynômes).
Sommaire
Définition
On appelle valuation une application d'un anneau commutatif unitaire
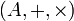 non nul vers un groupe abélien totalement ordonné (G, + , > ) union l'infini
non nul vers un groupe abélien totalement ordonné (G, + , > ) union l'infiniqui vérifie les propriétés suivantes :
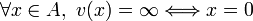 ;
;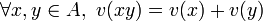 , autrement dit v est un morphisme de
, autrement dit v est un morphisme de 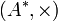 dans (G, + );
dans (G, + );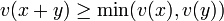 , ce qui est relié à l'inégalité triangulaire dans les espaces métriques.
, ce qui est relié à l'inégalité triangulaire dans les espaces métriques.
Notes :
- On utilise les conventions classiques
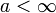 et
et 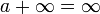 pour tout
pour tout 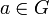 .
. - Certains auteurs se restreignent à une valuation sur un corps.
- On demande parfois à v d'être surjective.
Valuations discrètes
Lorsque
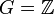 muni de l'addition, v est dite valuation de Dedekind ou valuation discrète. Deux valuations discrètes v1 et v2 sont équivalentes si et seulement elles sont proportionnelles, c'est-à-dire s'il existe un entier k tel que
muni de l'addition, v est dite valuation de Dedekind ou valuation discrète. Deux valuations discrètes v1 et v2 sont équivalentes si et seulement elles sont proportionnelles, c'est-à-dire s'il existe un entier k tel queou
Les classes d'équivalence des valuations discrètes sur un anneau A sont appelées places.
Valuation triviale
La valuation
est dite valuation triviale.
Propriétés
Propriétés générales
A est un anneau commutatif unitaire non nul muni d'une valuation v.
- v(1) = v( − 1) = 0
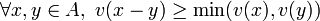
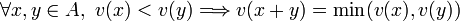
- A est intègre
- v se prolonge sur le corps des fractions Frac(A)
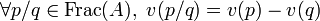
- la prolongation est unique.
- Soit
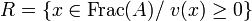 , alors
, alors
- R est un anneau intègre ;
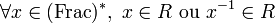
- Frac(A) = Frac(R)
Valuations discrètes sur l'ensemble des rationnels
Les places de
 , c'est-à-dire les valuations discrètes sur
, c'est-à-dire les valuations discrètes sur  à un facteur de proportionnalité près, sont:
à un facteur de proportionnalité près, sont:- la valuation triviale ;
- les valuations p-adiques (cf. exemple ci-dessous).
Valeur absolue associée
Soit v une valuation sur A à valeur dans
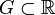 , et
, et ![\rho \in ]0,1[](/pictures/frwiki/50/29eb2711bb839c25779875bc5ee7e41a.png) . On associe à v la valeur absolue ultramétrique
. On associe à v la valeur absolue ultramétrique 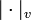 telle que
telle queExemples
Les applications suivantes sont des valuations.
Ordre d'annulation d'un polynôme
Article détaillé : Construction de l'anneau des polynômes.Soit K un corps (commutatif) et K[X] l'anneau des polynômes à coefficients dans K. Pour
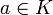 , on définit l'application
, on définit l'applicationqui à un polynôme P non nul associe le degré du plus petit monôme non nul de P(X − a) et à un polynôme nul, l'infini. Alors va(P) est l'ordre d'annulation de P en a; pour un polynôme à coefficients réels ou complexes, il s'agit du plus petit entier positif ou nul n tel que dP / dPn soit non nul.
Note : cela marche également pour a dans la clôture algébrique de K .
Ordre d'annulation d'une fraction rationnelle
Soit K un corps et K(X) le corps des fractions rationnelles à coefficients dans K. Soit
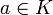 . On définit l'application
. On définit l'applicationqui à une fraction rationnelle associe la différences des ordres d'annulation du numérateur et du dénominateur en a. Si v(R) est positif, il s'agit de l'ordre d'annulation de R en a, si v(R) est strictement négatif, il s'agit de l'ordre du pôle de R en a.
Opposé du degré d'un polynôme
Soit K un corps et K[X] l'anneau des polynômes à coefficients dans K. On définit l'application
qui à un polynôme P associe l'opposé de son degré avec la convention
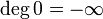 .
.Ordre d'une série de Laurent
- Sur le corps F((T)) des séries formelles de Laurent sur un corps commutatif F, on a une valuation en associant à tout série de Laurent son ordre en un élément donné de F.
Ordre d'une fonction méromorphe
- Si U est un ouvert connexe non vide du corps des nombres complexes et si a est un point de U, on a une valuation sur le corps des fonctions méromorphes sur U en associant à tout fonction méromorphe son ordre au point a'.
Valuation p-adique
Article détaillé : Nombre p-adique.Pour p un nombre premier, on définit l'application
qui à un entier n associe l'exposant de p dans la décompositon en nombres premiers de n, avec la convention
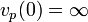 . L'application vp est appelée valuation p-adique sur
. L'application vp est appelée valuation p-adique sur 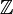 et se prolonge sur le corps des fractions
et se prolonge sur le corps des fractions  . Cette valuation définit la norme p-adique pour laquelle la clôture algébrique de
. Cette valuation définit la norme p-adique pour laquelle la clôture algébrique de  est l'ensemble des nombres p-adiques
est l'ensemble des nombres p-adiques  .
.Le point de vue métrique
Si v une valuation sur un corps K, alors l'application
est une distance sur K qui fait de K un corps topologique. On dit que K est complet pour v s'il est complet pour cette distance.
La complétion de K pour v est le procédé décrit ci-dessous :
- On note A l'anneau des suites de Cauchy de F, et on identifie les éléments de A aux suites constantes. La valuation de K se prolonge à A en une valuation encore notée v. L'ensemble I des suites de Cauchy tendant vers 0 est un idéal maximal de A sur lequel la valuation est triviale.
- Le quotient de A par I est un corps commutatif C, que l'on appelle complété de K pour v, et K s'identifie canoniquement à un sous-corps de C. On obtient sur C une valuation qui prolonge v. Le corps K est dense dans C, pour cette valuation sur C.
Par exemple,
 ou le corps k((T)) peuvent être obtenus par cette construction.
ou le corps k((T)) peuvent être obtenus par cette construction.Le point de vue algébrique
Soient K un corps commutatif et 'v une valuation sur K. Les éléments de K de valuation positive constituent un sous-anneau noté O. C'est un anneau local à valuation discrète, dont l'unique idéal maximal, constitué des éléments de valuation strictement positive, est noté M.
Par exemple, quand
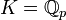 , on obtient
, on obtient 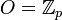 . Si F est un corps commutatif, pour K = F((T)), on obtient O = F[[T]].
. Si F est un corps commutatif, pour K = F((T)), on obtient O = F[[T]].Voir aussi
Liens internes
- Valeur absolue
- Anneau commutatif,anneau intègre, corps commutatif
- Corps des fractions
- Nombre p-adique
- Norme ultramétrique
- Portail des mathématiques
Catégorie : Théorie algébrique des nombres
Wikimedia Foundation. 2010.

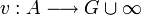
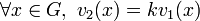
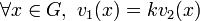
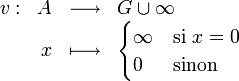
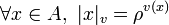
![\begin{array}{rrcl} v_a: & K[X]-\{0\} & \longrightarrow & \Z \cup \infty \\ & P & \longmapsto & \max\{k\in \N/\ \exists R \in K[X],\ P(X-a)=(X-a)^kR(X-a)\end{array}](/pictures/frwiki/54/69b98231d089a4715faadce29bd742b5.png)
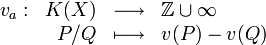
![\begin{array}{rrcl} v_\infty: & K[X] & \longrightarrow & \Z \cup \infty \\ & P & \longmapsto & -\deg P\end{array}](/pictures/frwiki/49/113478eb6f847e77bc0cf51169cf78b7.png)