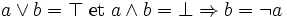- Algebre de Boole (structure)
-
Algèbre de Boole (structure)
En mathématiques, une algèbre de Boole ou un treillis booléen est un type de structure algébrique.
Sommaire
Définition
Une algèbre de Boole est un ensemble E contenant au moins deux éléments particuliers, notés
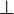 et
et 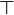 (ou 0 et 1), muni de deux lois de composition internes,
(ou 0 et 1), muni de deux lois de composition internes, 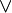 et
et  , et qui vérifie les axiomes suivants :
, et qui vérifie les axiomes suivants :- 1. associativité : Pour tous a, b et c de E,
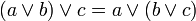 et
et 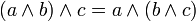
- 2. commutativité : Pour tous a et b de E,
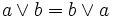 et
et 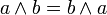
- 3. absorption : Pour tous a et b de E,
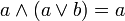 et
et 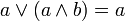
- 4. distributivité d'une loi par rapport à l'autre : Pour tous a, b et c de E,
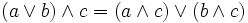 et
et 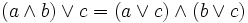
- 5. idempotence : Pour tout a de E,
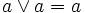 et
et 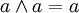
- 6. bornes : Pour tout a de E,
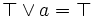 et
et 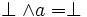
- 7. complémentarité : Pour tout a de E,
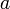 possède un complémentaire noté
possède un complémentaire noté 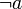 , tel que
, tel que 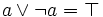 et
et 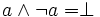
Les propriétés 1, 2, 3 et 5 définissent une structure de treillis, en particulier on définit un ordre, en posant
- a ≤ b si et seulement si a=a ∧ b, (ou de façon équivalente b = a ∨ b).
Les éléments
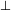 et
et 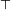 sont respectivement le plus petit et le plus grand élément du treillis. Ainsi, une algèbre de Boole est un treillis borné, distributif et complémenté.
sont respectivement le plus petit et le plus grand élément du treillis. Ainsi, une algèbre de Boole est un treillis borné, distributif et complémenté.Propriétés
Les propriétés suivantes se démontrent à partir des axiomes de la définition :
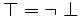 .
.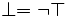 .
.- Pour tout a de E,
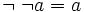 .
. - Pour tout a de E, le complémentaire est défini de manière unique. Autrement dit :
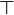 est l'élément neutre de la loi
est l'élément neutre de la loi  .
.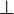 est l'élément neutre de la loi
est l'élément neutre de la loi 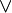 .
.- Pour tout a et b de E,
-
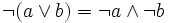 .
.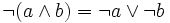
- (ces deux dernières formules sont les formules de De Morgan).
Exemples et applications des algèbres de Boole
L'algèbre de Boole binaire
L'algèbre de Boole la plus simple a deux éléments (une algèbre de Boole a au moins deux éléments). On peut la voir comme l'ensemble des valeurs de vérité {Vrai, Faux} muni des lois ET et OU. Elle permet d'interpréter les formules du calcul propositionnel. Le mathématicien britannique George Boole l'introduisit au milieu du XIXe siècle. On l'appelle aussi le Calcul booléen. Les opérations de l'algèbre de boole binaire sont implémentées sous forme de portes logiques dans les circuits électroniques et dans les microprocesseurs des ordinateurs.
Algèbres de Boole sur les ensembles
Les ensembles de parties d'un ensemble, munis des opérations d'union, d'intersection et de complémentation fournissent d'autres exemples d'algèbre de Boole (dont l'algèbre de Boole a deux éléments dans le cas des singletons).
Voir aussi
- Calcul des propositions
- Ensemblist, un jeu video qui utilise l'algèbre de Boole.
- Portail des mathématiques
- Portail de la logique
Catégorie : Structure algébrique
Wikimedia Foundation. 2010.