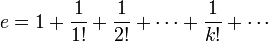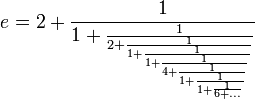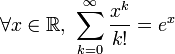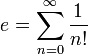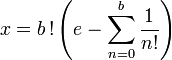- E (nombre)
-
e (nombre)
Article d'une série sur la constante mathématique e 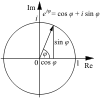
Logarithme naturel Applications Intérêts composés · Identité d'Euler et Formule d'Euler · Demi-vie et Croissance exponentielle/Décroissance exponentielle Définitions Démonstration de l'irrationalité de e · Représentations de e · Théorème de Lindemann-Weierstrass Personnes John Napier · Jacques Bernoulli · Leonhard Euler Conjecture de Schanuel  Pour les articles homonymes, voir E.
Pour les articles homonymes, voir E.e est une constante mathématique dont l'expression décimale commence par 2,718 281 828 459 045 235 360 287 4…. Il s'agit de la base des logarithmes naturels.
Appellation :
- e est parfois appelée constante de Néper, du nom du mathématicien écossais John Napier qui introduisit les logarithmes.
- e fut appelé nombre exponentiel par Euler en 1761.
Sommaire
Considérations historiques
Le nombre e est probablement la constante réelle la plus importante des mathématiques après π : on la retrouve en effet dans la normalisation des fonctions exponentielles. Il est cependant difficile de dater avec exactitude son apparition dans la littérature. En effet, si Neper introduit les logarithmes comme artifice de calcul pour simplifier les calculs du sinus, du cosinus, du produit et du quotient, il ne précise pas de base particulière pour ces logarithmes et les logarithmes les plus courants à cette époque sont ceux en base 10.
Les logarithmes naturels apparaissent pour la première fois en 1618 en appendice d'un traité de Napier probablement rédigé par William Oughtred.
En 1624, Briggs donne l'approximation du logarithme décimal d'un nombre qu'il n'identifie pas avec précision, mais qui se révèle être e.
En 1647, Grégoire de Saint-Vincent calcule l'aire sous l'hyperbole, mais ne met pas en évidence le nombre e.
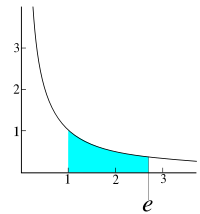
En 1661, Huygens est capable de faire le rapprochement entre l'aire sous l'hyperbole et les fonctions logarithmes. Comme e est le réel tel que l'aire sous l'hyperbole entre 1 et e vaille 1, il est probable que ce nombre fut remarqué à cette époque sans toutefois que l'on parle pour lui de la base du logarithme naturel.
La première apparition de e comme nombre remarquable date de 1683, époque à laquelle Bernoulli s'intéresse aux calculs d'intérêt. Ce qui l'amène à étudier la limite de la suite
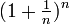 . Mais personne à ce moment ne fait le rapprochement entre ce nombre et les logarithmes naturels. Pourtant c'est durant cette période que l'on commence à entrevoir que la fonction logarithme de base a est la réciproque de la fonction exponentielle de base a. La communauté scientifique est alors mûre pour découvrir e. C'est dans une lettre de Leibniz à Huygens que ce nombre est enfin identifié comme la base du logarithme naturel, mais Leibniz lui donne le nom de b.
. Mais personne à ce moment ne fait le rapprochement entre ce nombre et les logarithmes naturels. Pourtant c'est durant cette période que l'on commence à entrevoir que la fonction logarithme de base a est la réciproque de la fonction exponentielle de base a. La communauté scientifique est alors mûre pour découvrir e. C'est dans une lettre de Leibniz à Huygens que ce nombre est enfin identifié comme la base du logarithme naturel, mais Leibniz lui donne le nom de b.On doit la notation e pour cette constante à Euler dans une lettre que celui-ci adresse à Goldbach en 1731. Le choix de e a donné lieu a de nombreuses conjectures : e pour Euler ? e pour exponentielle ? ou tout simplement e comme première voyelle disponible dans le travail d'Euler.
C'est aussi Euler qui donne le développement de e en série
et en fraction continue :
Puisque e possède un développement en fraction continue infini, il est irrationnel. Les différents approximants de Padé permettent d'offrir de nombreuses expressions de e sous forme de fractions continues généralisées (cf. l'article Approximant de Padé de la fonction exponentielle). Elles permettent à Charles Hermite de démontrer la transcendance de ce nombre en 1873.
Décimales connues
Le nombre de décimales connues de la constante e a augmenté de façon spectaculaire au cours des dernières décennies. Cette précision est due à l'augmentation des performances des ordinateurs ainsi qu'au perfectionnement des algorithmes[1],[2].
Nombre de décimales connues de la constante e Date Décimales connues Performance due à 1748 18 Leonhard Euler[3] 1853 137 William Shanks 1871 205 William Shanks 1884 346 J. Marcus Boorman 1946 808 ? 1949 2 010 John von Neumann (avec l'ENIAC) 1961 100 265 Daniel Shanks & John W. Wrench 1981 116 000 Stephen Gary Wozniak (avec l'Apple II[4]) 1994 10 000 000 Robert Nemiroff & Jerry Bonnell Mai 1997 18 199 978 Patrick Demichel Août 1997 20 000 000 Birger Seifert Septembre 1997 50 000 817 Patrick Demichel Février 1999 200 000 579 Sebastian Wedeniwski Octobre 1999 869 894 101 Sebastian Wedeniwski 21 novembre 1999 1 250 000 000 Xavier Gourdon 10 juillet 2000 2 147 483 648 Shigeru Kondo & Xavier Gourdon 16 juillet 2000 3 221 225 472 Colin Martin & Xavier Gourdon 2 août 2000 6 442 450 944 Shigeru Kondo & Xavier Gourdon 16 août 2000 12 884 901 000 Shigeru Kondo & Xavier Gourdon 21 août 2003 25 100 000 000 Shigeru Kondo & Xavier Gourdon 18 septembre 2003 50 100 000 000 Shigeru Kondo & Xavier Gourdon 27 avril 2007 100 000 000 000 Shigeru Kondo & Steve Pagliarulo Définitions et propriétés
Définitions de e
Les considérations précédentes montrent que e peut être défini de plusieurs façons différentes
- e est le réel tel que ln(e) = 1 lorsqu'on définit la fonction ln comme la primitive de la fonction
 qui s'annule en 1. C'est la raison pour laquelle cette constante est aussi appelée la base des logarithmes naturels
qui s'annule en 1. C'est la raison pour laquelle cette constante est aussi appelée la base des logarithmes naturels - e est le réel tel que exp(1) = e lorsqu'on définit la fonction exp comme l'unique fonction vérifiant u' = u et u(0) = 1.
- e est la limite de la suite
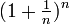 .
. - e est égal à la somme de la série infinie
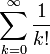 (avec la convention 0! = 1).
(avec la convention 0! = 1).
L'équivalence de ces quatre définitions provient des relations qui lient la fonction exponentielle, la fonction logarithme et les limites de suites.
Théorie des nombres
La constante de Néper apparaît largement dans la théorie des nombres. Les mathématiciens se sont très tôt intéressés à la nature du nombre e. L'irrationalité de e fut démontrée par Lambert en 1761 et plus tard par Euler. La démonstration peut se faire grâce à son développement en série (voir la démonstration de l'irrationalité de e, ci-dessous) soit par son développement en fraction continue.
La preuve de la transcendance de e fut établie par Hermite en 1873. On en déduit que, pour tout rationnel r non nul (ce qui inclut les entiers naturels), er est aussi transcendant, mais on ne sait pas encore (2007) si ee est transcendant ou non.
Les propriétés de ce nombre sont à la base du théorème de Lindemann-Weierstrass.
Il a été conjecturé que e était un nombre normal.
Fonction exponentielle et équation différentielle
Pour tout réel x, exp(x) = ex où exp est l'unique fonction y vérifiant l'équation différentielle y' = y et y(0) = 1. Cette fonction est appelée fonction exponentielle de base e.
Elle permet de donner toutes les solutions de l'équation différentielle y' = ay qui sont les fonctions définies par f(x) = Ceax.
La fonction exponentielle admet le développement en série suivant :
Fonction trigonométrique
La recherche de l'unique solution complexe à l'équation différentielle u' = iu et u(0) = 1 conduit à la fonction u(x) = eix = cos(x) + isin(x) et à l'identité d'Euler :
- eiπ + 1 = 0
qui selon Richard Feynman est « la formule la plus remarquable du monde »[5] (e représentant l'analyse, i l'algèbre, π la géométrie, 1 l'arithmétique et le nombre 0 les mathématiques). Euler lui-même aurait également été émerveillé de cette relation rassemblant cinq nombres fondamentaux : 0, 1, e, i, π.
Démonstration de l'irrationalité de e
Le nombre e est égal à la somme de la série de l'exponentielle de 1 :
Ce développement peut être employé pour montrer qu'il est irrationnel.
Démonstration, par l'absurde. Supposons qu'il existe deux entiers a et b tels que
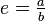 , où a est strictement positif et b strictement supérieur à 1. Considérons le nombre
, où a est strictement positif et b strictement supérieur à 1. Considérons le nombreNous allons démontrer que x est un nombre entier strictement positif et strictement inférieur à 1, et cette contradiction établira l'irrationalité de e.
-
- Pour voir que x est un nombre entier, remarquons que
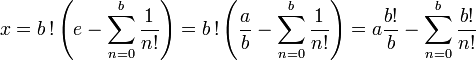
- Or, b divise b! et, pour tout entier n compris entre 0 et b, n! divise b!, les quantités
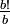 et
et 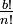 sont donc entières, x est donc entier comme somme et différence d'entiers.
sont donc entières, x est donc entier comme somme et différence d'entiers.
- Pour voir que x est un nombre strictement positif et strictement inférieur à 1, remarquons que
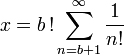 et ainsi
et ainsi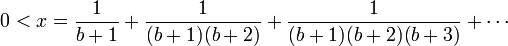

- Ici, la dernière somme est une série géométrique de raison
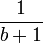 .
.
Puisqu'il n'existe aucun nombre entier strictement positif et strictement inférieur à 1, nous avons obtenu une contradiction, et ainsi e doit être irrationnel. ∎CQFD
Une autre démonstration consiste à établir le développement en fraction continue du nombre e. Si la preuve est plus complexe, elle offre aussi plus de possibilités de généralisation. Elle permet de montrer que si x est un nombre rationnel non nul, alors ex est irrationnel. Elle permet aussi d'établir que e n'est pas un irrationnel quadratique, c'est-à-dire n'est solution d'aucune équation du second degré à coefficients rationnels (cf. Fraction continue et approximation diophantienne). En revanche, pour aller plus loin, c'est-à-dire que pour montrer que e n'est solution d'aucune équation du troisième degré à coefficients rationnels, puis qu'il est transcendant, ce qui signifie qu'il n'est solution d'aucune équation polynomiale à coefficients rationnels, de nouvelles idées sont nécessaires.
Notes et références
- ↑ Sebah, P. and Gourdon, X.; (en)The constant e and its computation
- ↑ Gourdon, X.; (en)Reported large computations with PiFast
- ↑ (en)New Scientist 21st July 2007 p. 40
- ↑ (en)Byte Magazine vol. 6, Issue 6 (June 1981) p. 392) "The Impossible Dream: Computing e to 116,000 places with a Personal Computer"
- ↑ Equations as icons
Voir aussi
Articles connexes
Liens externes
- Démonstration de Fourier de l'irrationalité de e, présentée et analysée sur le site BibNum
- Démonstration d'Hermite de la transcendance de e (1873), présentée et analysée sur le site BibNum
- (en) John J. O'Connor et Edmund F. Robertson, The number e, MacTutor History of Mathematics archive.
- Portail des mathématiques
Catégories : Nombre transcendant | Analyse réelle | Constante mathématique | Exponentielle | Logarithme
Wikimedia Foundation. 2010.