Deuxième

---

2
Cardinal	Deux
Ordinal	deuxième second, seconde 2e
Préfixe grec	di
Préfixe latin	duo/bi
Adverbe	deuxièmement
Adverbe d'origine latine	secundo
Multiplicatif d'origine latine	bis
Propriétés
Facteurs premiers	2 (nombre premier)
Diviseurs	1, 2
Autres numérations
Numération romaine	II
Système binaire	10
Système octal	2
Système duodécimal	2
Système hexadécimal	2

2 (deux) est l'entier naturel suivant 1 et précédant 3.

Sommaire 1 Évolution du glyphe 2 Graphies actuelles 3 En mathématiques 4 Dans l'ethnologie 5 En sciences 6 Dans d'autre domaines 7 Voir aussi 7.1 Articles connexes 8 Liens externes

Évolution du glyphe

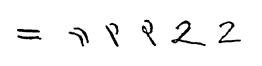
Le glyphe que nous utilisons aujourd'hui dans le monde occidental pour représenter le nombre 2 trouve ses racines chez les brahmanes hindous, qui écrivaient 2 sous forme de deux lignes horizontales (il est encore écrit de cette manière dans la Chine moderne, et est analogue au chiffre romain II). Les Gupta ont tourné les deux lignes à 45 degrés, pour en faire des diagonales. Ils ont aussi fait quelquefois une petite ligne au sommet et une fin incurvée à la base vers le centre de la ligne du bas. Apparemment pour aller plus vite, les Nagari ont démarré la ligne du haut plus incurvée et l'ont connecté à la ligne du bas. Les arabes Ghubar ont fait la ligne du bas complètement verticale, le glyphe ressemblait à un point d'interrogation sans point. En restaurant la ligne du bas dans sa position horizontale originale, mais en gardant la ligne du haut sous sa forme de courbe qui se connecte à cette première ligne cela nous conduit à notre glyphe moderne.

Graphies actuelles

La graphie « 2 » n'est pas la seule utilisée dans le monde ; un certain nombre d'alphabets — particulièrement ceux des langues du sous-continent indien et du sud-est asiatique — utilisent des graphies différentes.

Alphabet	Chiffre	Alphabet	Chiffre	Alphabet	Chiffre	Alphabet	Chiffre
Amharique	፪	Arabe	۲	Bengalî	২	Birman	၂
Devanāgarī	२	Gujarati	૨	Gurmukhî	੨	Kannara	೨
Khmer	໒	Latin	2	Malayalam	൨	Oriya	୨
Tamoul	௨	Télougou	౨	Thaï	๒	Tibétain	༢

En mathématiques

Deux possède beaucoup de propriétés en mathématiques. Un entier est appelé pair s'il est divisible par 2, c’est-à-dire sans reste. Sinon, il est qualifié d'impair. Pour les entiers écrits dans un système de numération basé sur un nombre pair, tel que le système décimal et hexadécimal, la divisibilité par 2 est facilement testée par un examen simple du dernier chiffre. S'il est pair, alors le nombre total est pair.

Deux est le plus petit et le premier nombre premier, et le seul pair. Malgré sa primalité, deux est aussi un nombre hautement composé, car il possède plus de diviseurs que un. Le nombre hautement composé suivant est 4.

Deux est un nombre intouchable.

Deux est un nombre premier super-singulier.

Deux est un facteur de 10, donc les fractions avec 2 dans le dénominateur ne donneront pas de développement décimal infini, comme c'est le cas avec la plupart des nombres premiers.

Quand on multiplie un nombre par 2, on a le double du nombre de départ. Quand on divise un nombre par 2, on a la moitié du nombre de départ.

Deux est la base du système de numération le plus simple dans lequel les nombres naturels peuvent être écrits de manière concise, le système binaire est largement utilisé dans les ordinateurs.

Pour tout nombre x :

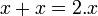 : de l'addition à la multiplication,

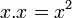 : de la multiplication à l'exponentiation,

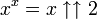 : de l'exponentiation aux puissances itérées de Knuth.

Les puissances de 2 sont centrales dans le concept des nombres premiers de Mersenne, et importants en informatique. 2 est le premier nombre premier de Mersenne mis en exposant.

Extraire une racine carrée d'un nombre est une opération mathématique tellement banale, que la place du signe de la racine où est placé l'exposant (par exemple 3 pour la racine cubique de x : ) est laissée blanche pour les racines carrées (exemple : 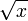), considérée comme tacite.

La racine carrée de 2 a été le premier nombre irrationnel connu par les pythagoriciens.

Le plus petit corps possède deux éléments.

Dans la construction théorique de l'ensemble des nombres naturels, 2 est identifié avec l'ensemble {0,1}. Ce dernier ensemble est important dans la théorie des catégories : c'est un classificateur de sous-objet dans la catégorie des ensembles.

Deux est une primorielle, en tant que sa propre factorielle. Deux apparait souvent dans des suites numériques, telles que les suites de Fibonacci, mais pas aussi souvent que un. Deux est aussi un nombre de Motzkin, le premier nombre premier de Sophie Germain, un nombre de Bell, un nombre Harshad complet, un nombre oblong, un nombre méandrique, un nombre semi-méandrique et un nombre méandrique ouvert.

Deux est le nombre de solutions du problème des n-dames pour n = 4.

Dans un polyèdre, on a toujours la relation suivante, qu'on peut démontrer : 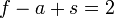(où f représente le nombre de faces, s le nombre de sommets et a le nombre d'arêtes). C'est la relation d'Euler. On obtient le même résultat en effectuant l'opération similaire en dimension 5, 7, 9 etc.

Dans l'ethnologie

La dualité de toutes choses est une notion importante dans la plupart des cultures et des religions. La dichotomie philosophique la plus commune est peut-être celle du bien et du mal, mais il en existe beaucoup d'autres. Voir le dualisme pour une vue d'ensemble. Dans la dialectique Hegellienne, le procédé de l'antithèse crée deux perspectives à partir d'une seule.

Deux (二, èr) est un bon nombre dans la culture chinoise. Un Chinois a dit « les bonnes choses vont par paires ». Par conséquent, il est commun d'utiliser des symboles en double dans la conception de noms de marques, c.a.d. double bonheur, double pièce, double éléphants etc. Les habitants de Canton aiment le nombre deux car il sonne comme le mot « facile » (易) en cantonais.

En Finlande, deux chandeliers sont allumés pour le jour de l'indépendance. En les mettant sur le bord de la fenêtre, on invoque le sens symbolique de la division, et ainsi de l'indépendance.

Dans la philosophie de Pythagore, la dyade est la deuxième chose créée (voir l'article monade pour plus de détails).

Le nombre 2 est quelquefois utilisé comme diminutif de « de ». De la même manière qu'en anglais d'ailleurs (two = to). Un exemple commun est un logiciel qui traduit des données d'un format dans un autre, tel que dvi2ps et texi2roff.

Les mots qui peuvent être utilisés comme synonymes de 2 incluent binôme, couple lorsque les deux nombres sont ordonnés, duo lorsque l'on parle de musiciens, paire lorsque les deux éléments sont distincts mais non ordonnés, et jumeaux lorsqu'ils sont mis en relation.

En sciences

Deux est :

• Le nombre de brins de polynucléotides dans une double-hélice d'ADN.
• Le premier nombre magique (physique).
• Le numéro atomique de l'hélium, un gaz noble.
• Le préfixe du système international pour 10⁶ est méga (M), et pour son inverse micro (µ).

Dans d'autre domaines

Groupes de deux :

• Listes de paires
  • liste de paires célèbres
  • liste des jumeaux

Deux est :

• Le nombre de la deuxième pièce des centimes d'euros où figure une Marianne, pour les pièces françaises.
• Le nombre de la dernière pièce d'euros où figure un chêne, un hexagone et la devise républicaine pour les pièces françaises.
• Le nom de plusieurs personnages fictifs : N° Deux.
• Dans la langue anglo-saxonne, la locution « number two », est un euphémisme pour la défécation (voir 1).
• Un des préfixes d'appel radio alloués au Royaume-Uni.
• Le numéro de la zone DVD pour l'Europe, l'Afrique du Sud, le Moyen-Orient et le Japon.
• Au rugby, le numéro de la position la plus dangereuse, le talonneur.
• Au baseball, deux représente la position du receveur.
• Le premier chiffre des codes d'appel téléphoniques en premier lieu pour les pays d'Afrique.
• La seconde dans le système scolaire français est la première classe du lycée.
• La deuxième planète du système solaire s'appelle Vénus.
• Le nombre de couleurs dans un jeu de cartes (rouge et noir).
• En France, le nombre d'années de mariage des noces de cuir.
• Dans les pays anglo-saxons et en Allemagne, le nombre d'années de mariage des noces de coton.
• En musique :
  • Dans l'échelle diatonique, la seconde — représentée de préférence par le chiffre arabe 2 — désigne un intervalle entre deux degrés conjoints. On pourra distinguer la seconde mineure, qui équivaut au demi-ton, et la seconde majeure, qui équivaut au ton.
  • Dans une gamme ou une tonalité, le chiffre romain II désigne, soit le deuxième degré — appelé sus-tonique —, soit la fonction tonale associée, soit l'accord correspondant — lorsqu'il est distingué, II = majeur et ii = mineur.
  • Dans la musique modale, le deuxième mode est appelé Dorien.
• En danse, utilisé dans l'expression pas de deux pour désigner une séquence chorégraphique qui réunit deux interprètes, nommée aussi duo.
• Années historiques : -2, 2, 1902 ou 2002.
• Le n° du département français, l'Aisne.
• Le numéro de l'autoroute française A2 qui part de Péronne (de l'A1) pour atteindre la Belgique.
• Le nombre d'atomes d'hydrogène dans une molécule d'eau (H₂O)

En anglais, 2 (two) est :

• La dénomination du billet de 2 $ où figure le portrait de Thomas Jefferson ; (dernière impression en 1996 ; en 2004, rarement vu en circulation).
• La dénomination de la pièce de 2 $ canadiens où figure un ours polaire.
• La dénomination de la pièce de 2 $ néo-zélandais, où figure le héron blanc.
• Une abréviation pour le mot « to » — leur prononciation se ressemble mais ce ne sont pas des homophones au sens strict, voir par exemple la phrase « from two to two to two two » (« de deux heures moins deux à deux heures deux ») ; ce mot a plusieurs sens, mais l'abréviation en général utilisée pour l'acception « vers » (direction, but), comme par exemple dans P2P (peer-to-peer) ou en langage SMS « 2U » (to you, pour toi).

Voir aussi