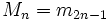Meandre (mathematiques)

Un méandre est, en mathématiques, une configuration dans le plan ℝ² formée par deux courbes planes simples se coupant transversalement. Intuitivement, un méandre peut être vu comme une route coupant une rivière à travers un certain nombre de ponts. On dit méandre ouvert dans le cas ou les deux courbes sont isotopes a des droites du plan et méandre fermé dans le cas ou une courbe est fermée et l'autre isotope a une droite.

Dans le cas ouvert, on peut toujours trouver une isotopie qui envoie une des deux courbes sur une ligne droite L.

Dans le cas ouvert, le nombre de points de croisements est un nombre entier positif n.

Dans le cas fermé, on peut toujours trouver une isotopie qui envoie la courbe non compacte sur une ligne droite L.

Dans le cas fermé, le nombre de points de croisements est un nombre entier positif pair 2n.

Deux méandres sont dits équivalents s'ils sont isotopes dans le plan ℝ².

Les méandres sont des objets difficiles à compter. On ne connaît pas de formule pour le nombre M_n de méandres ayant n intersections.

On peut colorier en noir et blanc les régions du plan déterminées par un méandre en alternant.

Sommaire 1 Nombres méandriques 2 Méandre ouvert 2.1 Exemples 2.2 Nombres méandriques ouverts 3 Semi-méandre 3.1 Exemples 3.2 Nombres semi-méandriques 4 Propriétés des nombres méandriques

Nombres méandriques

Le nombre de méandres distincts d'ordre n est le nombre méandrique M_n. Les quinze premiers nombres méandriques sont donnés ci-dessous suite A005315 de l’OEIS.

M₁ = 1

M₂ = 2

M₃ = 8

M₄ = 42

M₅ = 262

M₆ = 1 828

M₇ = 13 820

M₈ = 110 954

M₉ = 933 458

M₁₀ = 8 152 860

M₁₁ = 73 424 650

M₁₂ = 678 390 116

M₁₃ = 6 405 031 050

M₁₄ = 61 606 881 612

M₁₅ = 602 188 541 928

Méandre ouvert

Étant donnée une droite fixée orientée L dans le plan euclidien 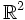, un méandre ouvert d'ordre n est une courbe orientée qui ne se coupe pas dans 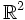qui coupe transversalement la droite à n points pour un certain entier positif n. Deux méandres ouverts sont dits équivalents s'ils sont homéomorphes dans le plan.

Exemples

Le méandre ouvert d'ordre 1 coupe la droite une fois :

Le méandre ouvert d'ordre 2 coupe la droite deux fois :

Nombres méandriques ouverts

Le nombre de méandres ouverts distincts d'ordre n est le nombre méandrique ouvert m_n. Les quinze premiers nombres méandriques ouverts sont donnés ci-dessous suite A005316 de l’OEIS.

m₁ = 1

m₂ = 1

m₃ = 2

m₄ = 3

m₅ = 8

m₆ = 14

m₇ = 42

m₈ = 81

m₉ = 262

m₁₀ = 538

m₁₁ = 1 828

m₁₂ = 3 926

m₁₃ = 13 820

m₁₄ = 30 694

m₁₅ = 110 954

Semi-méandre

Étant donnée une demi-droite R dans le plan euclidien 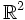, un semi-méandre d'ordre n est une courbe qui ne se coupe pas dans 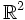qui coupe transversalement la demi-droite à n points pour un certain entier positif n. Deux semi-méandres sont dits être équivalents s'ils sont homéomorphes dans le plan.

Exemples

Le semi-méandre d'ordre 1 coupe la demi-droite une fois :

Fichier:Semi-meander M1 jaredwf.png

Le semi-méandre d'ordre 2 coupe la demi-droite deux fois :

Fichier:Meander M1 jaredwf.png

Nombres semi-méandriques

Le nombre de semi-méandres distincts d'ordre n est le nombre semi-méandrique M_n (généralement noté avec une ligne au-dessus à la place d'une ligne en-dessous). Les quinze premiers nombres semi-méandrique sont donnés ci-dessous suite A000682 de l’OEIS.

M₁ = 1

M₂ = 1

M₃ = 2

M₄ = 4

M₅ = 10

M₆ = 24

M₇ = 66

M₈ = 174

M₉ = 504

M₁₀ = 1 406

M₁₁ = 4 210

M₁₂ = 12 198

M₁₃ = 37 378

M₁₄ = 111 278

M₁₅ = 346 846

Propriétés des nombres méandriques

Il existe une fonction injective des nombres méandriques vers les nombres méandriques ouverts :

Chaque nombre méandrique peut être borné par des nombres semi-méandriques :

M_n ≤ M_n ≤ M_2n

Pour n > 1, les nombres méandriques sont pairs :

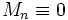(mod 2)

• Portail de la géométrie