- Nombre Premier Super-Singulier
-
Nombre premier super-singulier
En mathématiques, un nombre premier super-singulier est une certaine sorte de nombre premier.
Formellement, H désigne le demi-plan supérieur du plan complexe. Pour un nombre naturel n,
désigne le groupe modulaire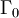 
, et soit 
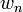l'involution de Fricke définie par la matrice bloc [[0, −1], [n, 0]]. De plus, soit la courbe modulaire 
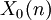étant la compactification (ajouté de points manquants) de
,
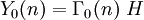et pour un nombre premier p quelconque, définissons
.
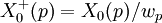Alors, p est super-singulier, ce qui signifie, par définition, que le genre de
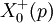est zéro.Il est aussi possible de définir les nombres premiers super-singuliers à la manière de la théorie des nombres en utilisant les courbes elliptiques super-singulières définies sur la clôture algébrique du corps fini GF(p) qui ont leur -invariant dans GF(p). Comme il apparaît, il existe exactement quinze nombres premiers super-singuliers : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59 et 71, voir suite A002267 de l’OEIS. Il peut aussi être montré que les nombres super-singuliers sont exactement les facteurs premiers de l'ordre du groupe Monstre M.
Note : l'ensemble des nombres premiers super-singuliers est un sous-ensemble de l'ensemble des nombres premiers de Chen.
Portail des mathématiques
Catégorie : Nombre premier
Wikimedia Foundation. 2010.
