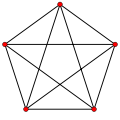
Théorème de Robertson-Seymour

En mathématiques, et plus précisément en théorie des graphes, le théorème de Robertson–Seymour (parfois également appelé le théorème des mineurs, et connu, avant qu'il soit démontré, sous le nom de conjecture de Wagner), est un théorème démontré en 2004 par Neil Robertson et Paul Seymour. Considéré généralement comme un des résultats les plus importants de la théorie des graphes, il se caractérise par une démonstration extraordinairement complexe et délicate, dont la publication, comportant plus de 500 pages, s'étala de 1983 à 2004 dans vingt articles de la revue Journal of Combinatorial Theory.

Le théorème de Robertson–Seymour affirme que « sur l'ensemble des graphes non orientés, l'ordre partiel défini par la relation « être un mineur » est un bel ordre ». Ce résultat est équivalent à dire que toute famille F de graphes fermée, c'est-à-dire telle que les mineurs des graphes de F appartiennent aussi à F, peut être caractérisée par un ensemble fini de « mineurs exclus », de la même manière que le théorème de Kuratowski caractérise les graphes planaires comme ceux dont aucun mineur n'est le graphe complet K₅, ni le graphe K_3,3 de l'énigme des trois maisons.

Bien que le théorème lui-même ne soit pas constructif (on ne connait d'ailleurs explicitement de listes de mineurs exclus que dans très peu de cas), Robertson et Seymour ont montré qu'il avait d'importantes conséquences en théorie de la complexité, garantissant l'existence d'algorithmes rapides pour de nombreux problèmes de décision.

Présentation informelle du théorème

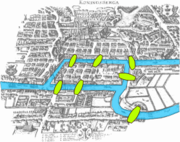
• Un célèbre exemple historique : la modélisation par Euler du problème des ponts de Königsberg.

La théorie des graphes est la discipline mathématique (et informatique) qui étudie les graphes, lesquels sont des modèles abstraits de dessins de réseaux reliant des points^{[note 1]}. Ces modèles sont constitués par la donnée de « points », appelés des sommets (en référence aux polyèdres), et de « liens » entre ces points ; ces liens, pour les graphes étudiés ici, sont symétriques (les graphes sont dits non orientés) et sont appelés des arêtes.

Un graphe ne peut pas toujours être dessiné sur une feuille de papier (ou, plus rigoureusement, dans un plan) sans que les arêtes se coupent ; quand c'est possible, le graphe est alors dit planaire. Ainsi, l'explication de l'impossibilité de l'énigme des trois maisons est que le graphe qui modélise l'énigme n'est pas planaire. En 1930, Kuratowski a obtenu une caractérisation de tous les graphes planaires, légèrement reformulée quelques années plus tard par Wagner, sous la forme d'une liste de deux graphes ne devant pas être « contenus » dans un graphe donné^{[note 2]} pour que ce dernier soit planaire.

• Les deux mineurs exclus des graphes planaires.
• 

  Le graphe complet K₅, ayant 5 sommets et 10 arêtes.

• 

  Le graphe biparti complet K_3,3, ayant 6 sommets et 9 arêtes.

Ce graphe à 14 sommets et 21 arêtes ne peut être tracé sur une feuille de papier sans que ses arêtes se coupent (il n'est pas planaire), mais peut être ainsi tracé sur un tore (un pneu) : on dit que c'est un graphe toroïdal.

Pour de nombreuses familles de graphes, par exemple ceux pouvant être dessinés sur la surface d'un pneu (en mathématiques, on parle de tore, et les graphes ainsi traçables sont les graphes toroïdaux), on peut se demander s'il existe une caractérisation analogue ; le théorème de Robertson-Seymour apporte une réponse affirmative à cette question, en énonçant que pour toute famille de graphes « fermée pour les mineurs » (le sens technique exact de cette expression sera détaillé plus loin), il existe une liste finie de graphes « interdits » caractérisant cette famille (mais, même pour des familles simples, comme celle des graphes toroïdaux, cette liste peut être très longue).

Historique

L'expansion d'un graphe est le résultat de l'ajout d'un ou plusieurs sommets sur une ou plusieurs arêtes, transformant par exemple l'arête •——• en les deux arêtes •—•—•.

En 1930, Kazimierz Kuratowski démontrait^[1] qu'un graphe était planaire s'il ne contenait pas de sous-graphe qui soit une expansion du graphe complet K₅, ou du graphe biparti complet K_3,3^{[note 3]}.

Quelques années plus tard, en 1937^[2], Klaus Wagner donnait une forme analogue^[3] mais équivalente^[4] de ce théorème, en caractérisant ces graphes comme ne contenant ni K₅ ni K_3,3 comme « mineurs ». Cette forme permet une généralisation facile à de nombreuses familles de graphes ayant une propriété analogue^{[note 4]}, par exemple « être traçable sur un tore », c'est pourquoi le théorème des mineurs, avant sa démonstration, était connu sous le nom de conjecture de Wagner (cependant, Wagner a par la suite affirmé qu'il n'avait jamais formulé lui-même cette conjecture, et avait d'ailleurs toujours pensé qu'elle devait être fausse^[5]).

Un résultat plus faible que cette conjecture, concernant seulement les arbres, découle du théorème de Kruskal^{[note 5]}, lequel avait été conjecturé en 1937 par Andrew Vázsonyi ; il fut démontré indépendamment en 1960 par Joseph Kruskal^[6] et S. Tarkowski^[7].

Entre 1983 et 2004, Neil Robertson et Paul Seymour développèrent sur une série de vingt articles publiés dans la revue Journal of Combinatorial Theory un plan de démonstration complet consistant entre autres à réduire progressivement le cas général à des cas particuliers plus simples^{[note 6]} (ainsi, le premier de leurs articles s'intitule Mineurs : exclusion d'une forêt et donne une démonstration d'une vingtaine de pages de ce que si l'un des mineurs exclus est une forêt^{[note 7]}, le théorème est vrai^[8]), mais introduisant également de nombreux concepts et outils nouveaux, comme la théorie de la décomposition arborescente^[9]. L'ensemble de la démonstration couvre au total plus de 500 pages^{[note 8]} ; la communauté mathématique en a validé le résultat^{[note 9]}, appelé désormais théorème de Robertson-Seymour^[10], pour lequel ils reçurent en 2006 le prix Fulkerson^[9] ; ce théorème, les outils développés pour sa démonstration, et ses conséquences algorithmiques inattendues, sont généralement considérés comme parmi les plus importants de la théorie des graphes^[11].

Le théorème de Robertson-Seymour

Définitions préliminaires

Un exemple de deux graphes, dont l'un (celui du dessous) est un mineur de l'autre. Le mineur a été obtenu en supprimant l'arête [e,f] et en contractant l'arête [b,c]

Un mineur d'un graphe non orienté G est un graphe pouvant être obtenu à partir de G par une suite (éventuellement vide) de contractions d'arêtes de G et de suppressions d'arêtes et de sommets de G^{[note 10]}.

La relation « H est un mineur de G » (qu'on notera par la suite H ≤ G) est une relation d'ordre partiel sur l'ensemble des graphes non orientés finis, considérés à isomorphisme près^{[note 11]} (si l'on ne considère pas les graphes isomorphes comme identiques, la relation n'est plus antisymétrique, et on obtient seulement un préordre^[12]).

Un ordre partiel (la terminologie est parfois appliquée également aux préordres, comme nous le ferons ici) est appelé un bel ordre s'il ne contient aucune suite infinie strictement décroissante (on dit que la relation d'ordre est bien fondée), ni aucune antichaîne infinie, c'est-à-dire aucun ensemble infini d'éléments incomparables deux à deux^{[note 12]} (définition qui généralise aux ordres partiels la notion de bon ordre définie pour les ensembles totalement ordonnés).

Formulations rigoureuses du théorème

Les définitions précédentes permettent de formuler rigoureusement le

L'existence d'une suite infinie décroissante étant évidemment impossible (puisque chaque mineur contient moins d'arêtes que le graphe précédent^[13]), ce théorème revient donc à affirmer qu'il n'y a pas d'ensemble infini de graphes deux à deux incomparables par la relation ≤  ; il convient cependant de remarquer que le théorème n'exclut nullement qu'il existe de tels ensembles finis aussi grands que l'on veut^{[note 13]}.

Utilisant la notion de graphe minimal d'un ensemble, c'est-à-dire tel qu'aucun autre graphe de l'ensemble n'en soit un mineur, on arrive à un énoncé équivalent au théorème, affirmant que dans tout ensemble de graphes, il n'y a (à isomorphisme près) qu'un nombre fini de graphes minimaux.

Une autre forme équivalente dit que dans tout ensemble infini de graphes, il existe un couple de graphes dont l'un est un mineur de l'autre^[13] (ce qui revient, par définition, à dire qu'il n'existe pas d'antichaînes infinies), ou encore, ce qui couvre également l'impossibilité de suites infinies décroissantes, que toute suite infinie G_i de graphes contient un couple tel que i < j et que G_i est un mineur de G_j^[14].

Familles fermées pour les mineurs

Une famille F de graphes est dite fermée (ou close) pour les mineurs (ce qui sera abrégé en famille fermée dans le reste de cet article) si chaque mineur d'un graphe de F appartient également à F^{[note 14]}. Dans le langage de la théorie des ordres, une famille fermée est donc une section commençante pour la relation « être un mineur ».

Caractérisation par mineurs exclus

Si F est une famille fermée, appelons S l'ensemble des graphes qui ne sont pas dans F (le complémentaire de F). Le théorème de Robertson–Seymour affirme l'existence d'un ensemble fini H formé des éléments minimaux de S^{[note 15]}. Ces éléments minimaux caractérisent F : les graphes de F sont exactement ceux n'admettant aucun graphe de H comme mineur^[15]. Les éléments de H sont appelés les mineurs exclus (ou interdits), ou encore les obstructions^{[note 16]}, pour la famille F.

Ainsi, les graphes planaires forment une famille fermée : les contractions et les suppressions d'arêtes d'un graphe planaire ne peuvent détruire sa planarité. Il en résulte que ces graphes peuvent être caractérisés par une famille finie de mineurs exclus, qui sont dans ce cas les deux graphes du théorème de Wagner : le graphe complet K₅ et le graphe biparti complet K_3,3.

L'existence d'une caractérisation par mineurs exclus de toutes les familles fermées est une affirmation équivalente au théorème de Robertson-Seymour. En effet, si S est un ensemble de graphes, appelons F la famille des graphes n'ayant pas de mineurs dans S. F est alors fermée, et son ensemble H de mineurs exclus est exactement l'ensemble des éléments minimaux de S (incomparables deux à deux), ce qui prouve que cet ensemble est fini^[16].

Exemples de familles fermées

Les familles de graphes (finis) suivantes^{[note 17]} sont fermées pour les mineurs, et par conséquent (d'après le théorème de Robertson–Seymour) possèdent des caractérisations par mineurs exclus (mais qu'on ne connait pas explicitement en général) :

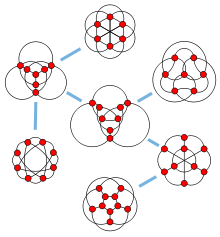La famille de Petersen, ensemble des sept obstructions correspondant aux graphes pouvant être plongés dans l'espace sans entrelacements^{[note 18]} (ces graphes sont incomparables en tant que mineurs, mais reliés les uns aux autres (comme indiqué par les traits bleus) par les transformations Y-Δ du théorème de Kennelly).

• les forêts (les graphes qui sont des unions d'arbres disjoints) ; on remarquera que les arbres eux-mêmes ne forment pas une famille fermée, un mineur d'un arbre n'étant pas forcément connexe ;
• les graphes planaires, les graphes toroïdaux, et, plus généralement, les graphes qui peuvent être tracés sur une surface donnée^[17] ;
• les graphes qui peuvent être plongés sans entrelacement^{[note 18]} ou sans nœud dans l'espace euclidien à 3 dimensions^[17] ;
• les graphes dont certains invariants^{[note 19]}, tels que la largeur arborescente, sont bornés par une constante finie fixée^{[note 20]}.

Ensembles d'obstructions

L’ensemble des obstructions pour une famille F donnée est défini comme l'ensemble des éléments minimaux (pour la relation de mineurs) du complémentaire de F, c'est-à-dire que c'est le plus petit ensemble de mineurs exclus caractérisant F ; le théorème de Robertson-Seymour affirme que cet ensemble est toujours fini quelle que soit F.

Des exemples d'ensembles d'obstructions finis étaient déjà connus (pour des classes de graphes particuliers) avant que le théorème de Robertson–Seymour soit démontré. Ainsi, la famille des forêts^{[note 7]} a pour seule obstruction le cycle à trois sommets (si l'on se restreint aux graphes simples), c'est-à-dire qu'un graphe est une forêt si et seulement s'il n'a pas ce cycle pour mineur. De même, le théorème de Wagner dit que l'ensemble des obstructions pour les graphes planaires est {K₅, K_3,3}. Un théorème analogue caractérise les graphes planaires extérieurs comme ayant pour obstructions les graphes K₄ et K_2,3.

Le théorème de Robertson-Seymour étend ces résultats à des familles fermées quelconques, mais, étant extrêmement non constructif, ne permet le plus souvent pas, même en principe^{[note 21]}, de déterminer l'ensemble des obstructions d'une famille donnée. Par exemple, l'ensemble des graphes toroïdaux (traçables sur un tore) est une famille fermée dont on ignore l'ensemble des obstructions ; on sait seulement qu'il comporte au moins 16 000 graphes^[18]. En 2011, on ne connait complètement l'ensemble des obstructions pour les familles de graphes traçables sur une surface donnée que dans le cas du plan (les deux graphes mentionnés plus haut) et dans le cas du plan projectif, où cet ensemble comporte 35 graphes^[19].

Algorithmes liés au théorème des mineurs

De nombreux questions d'informatique théorique sont modélisées par des graphes, ou plus précisément par la détermination de propriétés de certains graphes, un exemple célèbre étant le problème du voyageur de commerce.

La démonstration du théorème des mineurs a complètement changé l'estimation qu'on avait de la difficulté algorithmique de certains de ces problèmes. Ainsi, on ignorait jusque-là si la question de savoir si un graphe peut être plongé sans nœuds dans l'espace usuel était calculable, c'est-à-dire décidable par une machine de Turing ; on sait désormais qu'en fait, ce problème appartient à la classe P des problèmes solubles en temps polynomial, bien qu'on ne connaisse toujours aucun algorithme (même très lent) pour le résoudre^[20].

Reconnaissance en temps polynomial

Robertson et Seymour ont démontré que pour tout graphe fixé G, il existe un algorithme en temps polynomial qui teste si un graphe quelconque H possède G comme mineur^[21]. Plus précisément, cet algorithme demande un temps proportionnel au cube du nombre n des sommets et arêtes du graphe testé H (ce que l'on note O(n³) en notation de Landau). Ce résultat est moins utile en pratique qu'on ne pourrait le croire, parce que la constante de proportionnalité croît avec la taille de G de manière exponentielle. Il en résulte cependant que, pour toute famille fermée F, il existe un algorithme en temps polynomial décidant si un graphe donné G appartient ou non à F : il suffit de contrôler, pour chaque élément de l'ensemble des obstructions de F, s'il est ou non un mineur de G.

L'existence de cet algorithme est démontrée par le théorème de Robertson-Seymour, mais ce dernier ne donne aucun moyen effectif de le construire ; il est ainsi possible de démontrer qu'un problème peut être résolu en temps polynomial (dans le langage de la théorie de la complexité, on dit qu'il appartient à la classe P) sans pouvoir exhiber une telle solution : on dit qu'une telle preuve est non constructive^[22]. En revanche, dans de nombreux cas où l'ensemble des obstructions de F est connu explicitement, il est possible de savoir si un graphe appartient à F de manière plus efficace encore ; ainsi, tester si un graphe à n sommets est planaire peut être fait en temps linéaire^[23], c'est-à-dire en temps proportionnel à n.

Complexité paramétrée

Pour des invariants de graphes^{[note 19]} ayant la propriété que, pour un k fixé, la famille des graphes d'invariant plus petit que k est fermée^{[note 20]}, le même théorème s'applique ; c'est par exemple le cas de la largeur arborescente, ou du genre minimal de la surface sur laquelle le graphe peut être tracé. Dans chacun de ces cas, pour chaque k fixé, il y a un algorithme permettant, pour un graphe G ayant n sommets et arêtes, de déterminer si son invariant est ou non inférieur à k, en un temps inférieur à C(k)n³, où C(k) est une constante ne dépendant que de k et de l'invariant mesuré. Un problème ayant cette propriété (où n³ est remplacé par un polynôme quelconque) est dit soluble à paramètre fixé.

Cependant, cette méthode ne permet pas de construire un algorithme unique permettant de déterminer la valeur d'un tel invariant pour un graphe donné (lorsque cette valeur n'est pas bornée à l'avance), à cause de la difficulté qu'il y a à déterminer l'ensemble des obstructions. De plus, la constante C(k) augmente en général extrêmement vite avec k, rendant ces algorithmes très inefficaces en pratique. C'est pourquoi le développement d'algorithmes plus efficaces pour ces problèmes constitue encore en 2011 un important domaine de recherche.

Relation avec le problème P=NP

Le théorème des mineurs semble permettre de construire des algorithmes rapides (polynomiaux, et même cubiques) de résolution de problèmes dont on sait qu'ils sont NP-complets, voire NP-difficiles^[24]. Ainsi, le problème des chemins disjoints est NP-complet^{[note 22]}, mais Robertson et Seymour ont montré que, à k fixé, le problème des k chemins disjoints est effectivement soluble en temps polynomial^[25] ; cette contradiction apparente^{[note 23]} se résout en remarquant que le temps pris par l'algorithme est un polynôme en n (la taille du graphe étudié) de la forme C(k)n³, comme on l'a vu dans la section précédente, mais que la constante C(k) augmente au moins exponentiellement avec k, et que c'est elle qui définit la complexité algorithmique du problème des chemins disjoints.

Bien que le théorème de Robertson-Seymour n'ait pas vraiment apporté d'informations nouvelles concernant le problème P=NP, Fellows et Langston ont fait remarquer^[26] que leur démonstration non constructive d'existence d'algorithmes polynomiaux (et où apparaissent souvent, qui plus est, des constantes de proportionnalité bien trop grandes pour qu'ils puissent avoir une utilisation pratique quelconque) rend moins claire qu'auparavant la distinction entre algorithmes polynomiaux (considérés comme utilisables de manière réaliste) et non polynomiaux (à jamais inutilisables pour des ensembles de données un peu vastes), et donc que l'intuition de la majorité des informaticiens^{[note 24]}, selon laquelle la classe P est différente de la classe NP, pourrait bien s'avérer fausse, sans pour autant que les problèmes NP-complets en deviennent faciles à résoudre.

Conséquences en logique mathématique

L'étude de la logique mathématique, c'est-à-dire l'analyse systématique des fondations des mathématiques et des bases logiques sur lesquelles s'appuient les démonstrations, commencée à la fin du dix-neuvième siècle par des logiciens et des mathématiciens tels que Gottlob Frege et Giuseppe Peano, a amené vers 1930 à la découverte de surprenants résultats d'indécidabilité, liés aux célèbres théorèmes d'incomplétude de Gödel ; ces résultats, dont la forme générale est « la théorie T ne permet pas de démontrer l'affirmation A, ni sa négation non A », sont souvent dits méta-mathématiques, car ils portent sur les mathématiques elles-mêmes et non sur les objets mathématiques usuels. La plupart des affirmations A ainsi construites étaient généralement jugées artificielles^{[note 25]}, et des énoncés plus conformes à la pratique courante des mathématiciens semblaient ne pas devoir susciter de tels problèmes. Pourtant, vers 1980, Jeff Paris^[27] a obtenu des énoncés de forme apparemment naturelle et inoffensive, par exemple affirmant qu'une certaine suite finit par décroître^{[note 26]}, mais revenant en fait à définir des entiers si grands que leur « existence » ne peut être prouvée à l'aide des seuls axiomes de Peano ; cela implique que, en n'utilisant que ces axiomes, les énoncés en question sont indécidables.

En 1987, Friedman, Robertson et Seymour ont montré que, si le théorème des mineurs était vrai, le théorème suivant (qui en est un cas particulier^{[note 27]}) serait lui aussi, et pour les mêmes raisons, non démontrable dans des systèmes beaucoup plus forts que l'arithmétique de Peano^[28], bien qu'il soit démontrable dans ZFC (et en fait, l'analyse détaillée de la preuve de Robertson et Seymour permet de montrer qu'il est démontrable dans des systèmes beaucoup moins puissants que ZFC) :

Théorème : Pour tout entier n, il existe un entier m si grand que si G₁, ..., G_m est une suite de graphes finis non orientés, où chaque G_i a au plus n+i sommets et arêtes, alors il existe j < k tels que G_j soit un mineur de G_k.

Là encore, l'entier m est une fonction de n à croissance si rapide^{[note 28]} que les axiomes de Peano (ou même des formes très renforcées de ces axiomes) ne permettent pas de montrer qu'elle est toujours définie, ce qui explique ces résultats d'indécidabilité ; on trouvera dans l'article théorème de Kruskal une description plus précise d'autres théorèmes de logique mathématique analogues, dus eux aussi à Friedman. Ces théorèmes donnent ainsi des exemples de propositions indécidables en arithmétique, considérées comme plus naturelles que celles correspondant au théorème de Gödel^[29].

Généralisations : hypergraphes et graphes infinis

En 2011, Robertson et Seymour ont achevé la démonstration d'un résultat analogue sur les hypergraphes^[30], définissant un préordre similaire à la relation de mineur, et montrant qu'il s'agit là encore d'un bel ordre. Parmi les conséquences de ce résultat, ils en déduisent que le théorème des mineurs (pour les graphes) s'applique encore si on munit les sommets ou les arêtes d'étiquettes (elles-mêmes ordonnées par un bel ordre), et qu'on demande aux mineurs de respecter l'ordre de ces étiquettes^{[note 29]}. Ce résultat leur a également permis de démontrer une conjecture de Nash-Williams  : dans toute suite infinie de graphes, il en existe deux tels que le premier peut être immergé dans le second^{[note 30]}.

Il n'est pas impossible qu'un théorème analogue soit encore vrai pour des graphes infinis dénombrables, mais cette conjecture (ou d'ailleurs sa réfutation) est considérée comme encore plus difficile que ne l'est le théorème des mineurs ; Reinhard Diestel pense qu'elle pourrait être liée à une autre conjecture de Seymour, affirmant que tout graphe infini dénombrable possède un mineur (strictement plus petit) qui lui est isomorphe^[31]. En revanche, on sait que ce résultat est faux pour des graphes non dénombrables : Péter Komjáth a démontré que, si λ est un cardinal non dénombrable, il existe 2^λ graphes de cardinal λ dont aucun n'est un mineur de l'autre^{[32],[note 31]}

Notes et références

Notes

Références

Bibliographie

Livres

• (en) Daniel Bienstock et Michael A. Langston, « Algorithmic implications of the graph minor theorem », dans Network Models, coll. « Handbooks in Operations Research and Management Science » (n^o 7), 1995 [lire en ligne], p. 481–502  [PDF].
• (en) John Chambers, Hunting for torus obstructions, M.Sc. thesis, Department of Computer Science, UVic, 2002 .
• (en) Reinhard Diestel, Graph Theory, Springer, 2005 [lire en ligne], p. 326–367  [PDF].
• (en) Harvey Friedman, Neil Robertson et Paul Seymour, « The metamathematics of the graph minor theorem », dans S. Simpson, Logic and Combinatorics, AMS, coll. « Contemporary Mathematics » (n^o 65), 1987, p. 229–261 .

Articles provenant de publications scientifiques

• Jean-Paul Delahaye, « Une propriété cachée des graphes », dans Pour la Science, vol. avril, n^o 3, 2008, p. 92-97 .
  Article de vulgarisation.

• (en) László Lovász, « Graph Minor Theory », dans Bull. Amer. Math. Soc. (New Series), vol. 43, n^o 1, 2005, p. 75–86 [texte intégral]  [PDF].
• (en) Michael R. Fellows et Michael A. Langston, « Nonconstructive tools for proving polynomial-time decidability », dans Journal of the ACM, vol. 35, n^o 3, 1988, p. 727–739 [lien DOI] .
• (en) Michael R. Fellows et Michael A. Langston, « On search, decision, and the efficiency of polynomial-time algorithms », dans Journal of Computer and System Sciences, vol. 49, n^o 3, 1994, p. 769–779 .
  En voici un résumé étendu [PDF], dû aux auteurs eux-mêmes.
• (en) Neil Robertson et Paul Seymour, « Graph Minors. I. Excluding a forest », dans Journal of Combinatorial Theory, Series B, vol. 35, n^o 1, 1983, p. 39–61 [lien DOI] .
  Le premier des vingt articles de la démonstration complète, intitulé Mineurs : exclusion d'une forêt.
  En 1995, Reinhard Diestel a publié une preuve simplifiée de ce résultat, dans un article de quatre pages disponible en ligne [PDF].
• (en) Neil Robertson et Paul Seymour, « Graph Minors. XIII. The disjoint paths problem », dans Journal of Combinatorial Theory, Series B, vol. 63, n^o 1, 1995, p. 65–110 [lien DOI] .
• (en) Neil Robertson et Paul Seymour, « Graph Minors. XX. Wagner's conjecture », dans Journal of Combinatorial Theory, Series B, vol. 92, n^o 2, 2004, p. 325–357 [texte intégral]  [PDF].
• (en) Neil Robertson et Paul Seymour, « Graph Minors. XXIII. Nash-Williams’s immersion conjecture », dans Journal of Combinatorial Theory, Series B, vol. 100, n^o 2, 2010, p. 181–205 [texte intégral]  [PDF].

Voir aussi

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Robertson-Seymour theorem » (voir la liste des auteurs)

Articles connexes

• Bel ordre
• Graphe planaire
• Lemme de Higman
• Théorème de Kruskal

Liens externes

• Sur le site professionnel de Eric Thierry (Maître de conférences à l'ENS Lyon), on trouvera en particulier un exposé rigoureux de Bastien Legloannec, en français [PDF], contenant des démonstrations complètes des propriétés des beaux ordres (en passant par le théorème de Ramsey infini, qu'il démontre également), une démonstration du théorème de Kruskal dans le cas des arbres non étiquetés, et beaucoup d'exemples et de contre-exemples.

• Portail de la géométrie
• Portail de l'informatique théorique

Le 6 novembre 2011, Théorème de Robertson-Seymour a été proposé pour être reconnu comme « article de qualité ». Vous pouvez donner votre avis sur cette proposition. Suivi des modifications de l'article depuis la proposition.