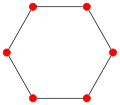
Graphe cycle

Graphe cycle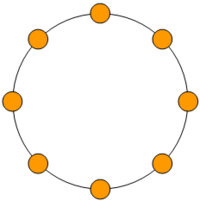
Page d'aide sur l'homonymie Ne doit pas être confondu avec Graphe des cycles ni Cycle (théorie des graphes).
Graphe cycle
Intercpunetring.png
C8
Notation Cn
Nombre de sommets n
Nombre d'arêtes n
Distribution des degrés 2-régulier
Diamètre n / 2
Propriétés Hamiltonien
Eulérien
Planaire
Distance-unité
Symétrique
Graphe de Cayley
modifier Consultez la documentation du modèle

Les graphes cycles, ou n-cycles, forment une famille de graphes. Le graphe cycle Cn est constitué d'un unique cycle élémentaire de longueur n (pour n \geq 3). C'est un graphe connexe non-orienté d'ordre n à n arêtes. Il est 2-régulier, c'est-à-dire que chacun de ses sommets est de degré 2[1].

Sommaire

Terminologie

Beaucoup de termes sont employés pour désigner le graphe cycle : n-cycle, polygone et n-gone. Le terme de graphe cyclique est parfois employé, mais il pose problème car il s'oppose normalement à graphe acyclique.

Propriétés fondamentales

  • Nombre chromatique. Le nombre chromatique du cycle Cn est égal à 3 si n est impair, à 2 sinon. En d'autres termes, Cn est biparti si et seulement si n est pair.
  • Connexité. Par construction Cn est connexe. Il est facile de constater qu'il est 2-sommet-connexe (c'est-à-dire qu'il cesse d'être connexe uniquement quand on lui supprime 2 sommets). Il est également 2-arête-connexe.
  • Hamiltonicité. L'unique cycle contenu dans Cn est un cycle hamiltonien. Le graphe est donc hamiltonien.
  • Planarité. Cn est un graphe planaire.
  • Eulérien. Étant 2-régulier, le cycle Cn est eulérien par le théorème d'Euler-Hierholzer.
  • Line graph. Le line graph (en) de Cn est isomorphe à Cn.

Aspects algébriques

Le graphe cycle Cn peut être dessiné comme un polygone régulier à n sommets. Les isométries de ce polygone s'avèrent alors êtres des automorphismes de Cn. De là découlent l'arête-transitivité et la sommet-transitivité. Cn est donc un graphe symétrique. Tous ses sommets et toutes ses arêtes jouent le même rôle en termes d'isomorphisme de graphe.

Il est facile de constater que seules les isométries de ce polygone sont des automorphismes valides de Cn. Le groupe d'automorphisme du graphe cycle Cn est donc isomorphe à celui des isométries du polygone régulier à n sommets, à savoir le groupe diédral Dn, groupe d'ordre 2n[2].

Le graphe cycle Cn est un graphe de Cayley[3] avec :

G = {\frac {\mathbb Z}{n {\mathbb Z}}}
S = {1,n − 1}

Cas particuliers

Galerie

  • C3

  • C4

  • C5

  • C6

Références

  1. ↑ Eric W. Weisstein, Cycle Graph at MathWorld.
  2. ↑ Kenneth H. Rosen, John G. Michaels. Handbook of Discrete and Combinatorial Mathematics. CRC Press, 2000.
  3. ↑ In theory: Characters and Expansion by Luca Trevisan

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Graphe cycle de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Cycle hamiltonien — Graphe hamiltonien En théorie des graphes, un graphe hamiltonien est un graphe possédant au moins un cycle passant par tous les sommets une et une seule fois. Un tel cycle élémentaire est alors appelé cycle hamiltonien. Un graphe hamiltonien ne… …   Wikipédia en Français

  • Graphe Hamiltonien — En théorie des graphes, un graphe hamiltonien est un graphe possédant au moins un cycle passant par tous les sommets une et une seule fois. Un tel cycle élémentaire est alors appelé cycle hamiltonien. Un graphe hamiltonien ne doit pas être… …   Wikipédia en Français

  • Graphe roue — Quelques exemples de graphe roue. Notation Wn Nombre de sommets n Nombre d arêtes 2(n …   Wikipédia en Français

  • Cycle (Graphe) — Pour les articles homonymes, voir Cycle. Dans un graphe non orienté, un cycle est une suite d arêtes consécutives (chaîne) dont les deux sommets extrémités sont identiques. Si la chaîne est élémentaire, c est à dire ne passe pas deux fois par un… …   Wikipédia en Français

  • Cycle (graphe) — Pour les articles homonymes, voir Cycle. Dans un graphe non orienté, un cycle est une suite d arêtes consécutives (chaîne) dont les deux sommets extrémités sont identiques. Si la chaîne est élémentaire, c est à dire ne passe pas deux fois par un… …   Wikipédia en Français

  • Graphe triangle — Représentation du graphe triangle. Notation C3, K3 Nombre de sommets 3 Nombre d arêtes 3 Distribution des degrés 2 ré …   Wikipédia en Français

  • Graphe de Hoffman-Singleton — Schéma du graphe de Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés …   Wikipédia en Français

  • Graphe diamant — Représentation du graphe diamant. Nombre de sommets 4 Nombre d arêtes 5 Distribution des degrés 2 (2 sommets) 3 (2 sommets) Rayon 1 …   Wikipédia en Français

  • Graphe criquet — Représentation du graphe criquet. Nombre de sommets 5 Nombre d arêtes 5 Distribution des degrés 1 (2 sommets) 2 (2 sommets) 4 (1 sommet) Rayon 1 …   Wikipédia en Français

  • Graphe taureau — Représentation du graphe taureau. Nombre de sommets 5 Nombre d arêtes 5 Distribution des degrés 1 (2 sommets) 2 (1 sommet) 3 (2 sommets) Rayon …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”