- Klaus Wagner
-
Pour les articles homonymes, voir Wagner.
Klaus Wagner et Frank Harary à Oberwolfach, 1972.
Klaus Wagner né le 31 mars 1910 mort le 6 février 2000 fut un mathématicien allemand.
Il étudia la topologie à l'université de Cologne sous la supervision de Karl Dörge, lui-même ancien étudiant d'Issai Schur[1]. Wagner reçut son doctorat en 1937 et enseigna à Cologne pendant de nombreuses années. En 1970, il changea pour l'université de Duisburg où il resta jusqu'à sa retraite, en 1978. En juin 2000, à la suite de son décès, l'université de Cologne organisa un colloque en sa mémoire[2].
Mineurs de graphes
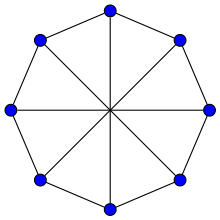
Le graphe de Wagner, ou l'échelle de Möbius à 8 sommets.Wagner est connu pour ses contributions à la théorie des graphes et en particulier pour les mineurs de graphes. Son théorème caractérise les graphes planaires comme étant ceux qui n'ont ni le graphe complet K5, ni le graphe biparti complet K3,3 comme mineur. Ceci est relié, mais différent, du théorème de Kuratowski qui dit que les graphes planaires sont ceux dont les graphes ne contiennent pas une subdivision de K5 ou K3,3,. Un de ses autres résultats, connu sous le nom de Théorème de Wagner, est qu'un graphe 4-connexe est planaire si et seulement s'il n'a pas K5 comme mineur. Ceci implique une caractérisation des graphes sans K5 comme mineur : ils sont construits à partir de graphes planaires et de l'échelle de Möbius à 8 sommets (parfois appelée graphe de Wagner) par somme de cliques. Wagner utilisa ensuite cette caractérisation pour montrer que le cas k = 5 de la conjecture d'Hadwiger sur le nombre chromatique de graphes sans mineur Kk est équivalent au théorème des quatre couleurs. Des décompositions plus compliquées de graphes en sommes de cliques de graphes plus simples, généralisant ce résultat, sont depuis devenues standard dans les travaux sur les mineurs.
Wagner émit dans les années 1937 la conjecture[3] que, dans tout ensemble infini de graphes, un graphe est isomorphe au mineur d'un autre ; cette conjecture ne fut publiée que bien plus tard. L'essence de cette conjecture est que toute famille de graphes, close par mineur, peut automatiquement être caractérisé par un ensemble fini de mineurs interdits, tels que le théorème qui caractérise les graphes planaires. Neil Robertson et Paul Seymour publièrent une preuve de cette conjecture en 2004, connue sous le nom de théorème de Robertson-Seymour[4].
Notes et références
- (en) Généalogie mathématique de Klaus Wagner, accédé le 16 février 2009.
- (en) Annonce du colloque à la mémoire de Klaus Wagner, accédé le 16 février 2009.
- (en) Bill Casselman - Variations on graph minor, essais de l'American Mathematical Society, accédé le 16 février 2009.
- (en) Neil Robertson et Paul Seymour - Graph Minors XX : Wagner's Conjecture, Journal of Combinatorial Theory, série B, volume 92, pages 325-357, 2004.
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Klaus Wagner (mathematician) » (voir la liste des auteurs)
Catégories :- Personnalité en théorie des graphes
- Naissance en 1910
- Décès en 2000
- Mathématicien allemand
- Topologue
Wikimedia Foundation. 2010.
