Section commençante

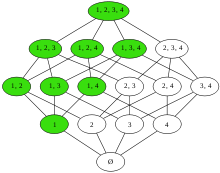Le treillis de l'ensemble des parties de l'ensemble {1,2,3,4}, la section finissante étant colorée en vert.

En mathématiques, et plus précisément en théorie des ordres, une section commençante (parfois également appelée sous-ensemble fermé inférieurement) d'un ensemble ordonné (X,≤) est un sous-ensemble S de X tel que si x est dans S et si y≤x, alors y est dans S.

Dualement, on appelle section finissante (ou sous-ensemble fermé supérieurement) un sous-ensemble F tel que si x est dans F et si x≤y, alors y est dans F.

Exemples

Dans le cas d'un ensemble totalement ordonné, les sections commençantes sont des intervalles ; en particulier, dans le cas de l'ensemble R des nombres réels, les sections commençantes non vides et non identiques à R sont les intervalles de l'une des deux formes et .

Pour la relation d'inclusion, l'ensemble des sous-ensembles d'un ensemble donné X est une section commençante de l'ensemble des parties de Y, pour tout Y tel que .

Par définition, pour la relation d'inclusion, l'ensemble des voisinages d'un point d'un espace topologique est une section finissante de l'ensemble des parties de cet espace.

Propriétés

Dans la liste de propriétés suivante, on peut partout remplacer section commençante par section finissante (en échangeant au besoin maximum et minimum, etc.)

• Tout ensemble ordonné est section commençante de lui-même.
• L'intersection et l'union d'une famille de sections commençantes sont des sections commençantes.
• Le complémentaire d'une section commençante est une section finissante.
• Étant donné un ensemble ordonné (X,≤), la famille des sections commençantes de X, ordonnée par inclusion, est un treillis complet, le treillis commençant O(X).
• Étant donné un sous-ensemble arbitraire Y d'un ensemble ordonné X, l'intersection des sections finissantes contenant Y est la plus petite de ces sections finissantes, notée ↑Y.
  • De même, la plus petite section commençante contenant Y est notée ↓Y.
• Une section finissante de X est dite principale si elle est de la forme ↑{x}, où x est un élément de X ; deux applications importantes de cette terminologie correspondent au cas des idéaux et à celui des ultrafiltres.
• L'ensemble des éléments minimaux d'une section finissante forme une antichaîne.
  • Réciproquement, toute antichaîne A détermine une section finissante {x / il existe un y de A tel que x ≥ y}. Pour des ordres partiels satisfaisant une condition de chaîne descendante, cette correspondance entre antichaînes et sections finissantes est une bijection(mais ce n'est pas le cas en général pour un ordre partiel quelconque).

Le cas des ordinaux

Un ordinal peut être identifié avec l'ensemble des ordinaux qui lui sont strictement inférieurs. Chaque ordinal s'identifie alors à une section commençante de la classe de tous les ordinaux, ordonnés par inclusion.

Voir aussi

• Intervalle
• Paradoxe de Burali-Forti

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Upper set » (voir la liste des auteurs)

• N. Bourbaki, Éléments de mathématique – Théorie des ensembles, ch. III, § 1, n° 2, p. 3, pour les définitions et les premières propriétés des ordres partiels.
• (en) J. Blanck, « Domain representations of topological spaces », dans Theoretical Computer Science, vol. 247, 2000, p. 229–255
• (en) K. H. Hoffman, The low separation axioms (T₀) and (T₁), 2001
• (en) B. A. Davey et H. A. Priestley, Introduction to Lattices and Order, Cambridge University Press, 2002, 2^e éd. (ISBN 0-521-78451-4) 

• Portail des mathématiques