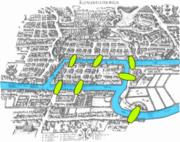
Probleme des sept ponts de Konigsberg

Le problème des sept ponts de Königsberg est le suivant :

→ →

La ville de Königsberg (aujourd'hui Kaliningrad) est construite autour de deux îles reliées entre elles par un pont et six ponts relient le continent à l'une ou l'autre des deux îles. Le problème consiste à déterminer s'il existe ou non une promenade dans les rues de Königsberg permettant, à partir d'un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ, étant entendu qu'on ne peut traverser le Pregel qu'en passant sur les ponts.

Résolution du problème

Une telle promenade n'existe pas, et c'est Euler qui donna la solution de ce problème en caractérisant les graphes que l'on appelle aujourd'hui « eulériens » en référence à l'illustre mathématicien.

Ce problème n'a qu'un intérêt historique, et absolument aucun intérêt mathématique en dehors de sa généralisation à tous les graphes, car pour ce cas, il est assez intuitif de démontrer que la promenade demandée n'existe pas. Pour voir cela, il suffit d'associer un graphe à la ville comme dans la figure ci-dessus et de supposer que la promenade recherchée existe. On peut alors, à partir de la promenade, ordonner les sept arêtes du graphe de façon à ce que deux arêtes consécutives par rapport à notre ordre soient adjacentes dans le graphe (en considérant que la dernière et la première arête sont consécutives, puisqu'il y a retour au point de départ).

Ainsi tout sommet du graphe est-il nécessairement incident à un nombre pair d'arêtes (puisque s'il est incident à une arête il est aussi incident à l'arête précédente ou qui lui succède dans l'ordre). Mais le graphe a des sommets qui sont incidents à trois arêtes, d'où l'impossibilité.

Notons que même si on renonce à exiger le retour au point de départ, une promenade traversant une et une seule fois chaque pont n'existe pas. Elle existerait si seuls deux sommets du graphe, correspondant aux points à choisir respectivement comme départ et arrivée, étaient incidents à un nombre impair d'arêtes. Or les sommets du graphe des ponts de Königsberg sont tous les quatre dans ce cas, on est donc loin du compte. Il suffirait cependant de supprimer ou de rajouter un pont quelconque pour que le graphe modifié permette des promenades tous ponts sans retour (seuls deux sommets restant d'incidence impaire). Et ce sont au moins deux ponts, bien choisis, qu'il faudrait ajouter ou retirer pour permettre la promenade avec retour initialement visée.

Sources

• Léonard Euler, « Solutio problematis ad geometriam situs pertinentis » (1759), in Mémoires de l'Académie des sciences de Berlin
• Édouard Lucas, Récréations mathématiques, vol. I (1882), éd. Gauthier Villars, Paris : le « problème des sept ponts » fait l'objet de la « récréation n° 2 ».

Articles connexes

• Graphe eulérien
• Nœud gordien
• Œuf de Colomb
• Problème des neuf points

• Portail des mathématiques
• Portail de la logique