Antichaine

Antichaine

Antichaîne

Une antichaîne, A est une partie d'un ensemble, E, muni d'une relation d'ordre partiel (ici 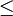\leq ) telle que

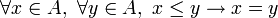\forall x \in A, \ \forall y \in A,\ x \leq y \rightarrow x=y.

Plus intuitivement, on peut voir une antichaine comme une partie d'un ensemble, muni d'une relation d'ordre, dont les éléments sont deux à deux incomparables.

Antichaînes de N

Il s'agit des antichaînes de N pour la divisibilité qui est évidemment une relation d'ordre partiel sur N. Soit E une partie non vide de N, une antichaîne de N contenue dans E s'appelle également une antichaîne de E

Soit n un entier naturel non nul fixé et E2n = {1,2,...2n}. On démontre que le maximum des cardM lorsque M parcourt l'ensemble des antichaînes de E2n est n . Nous

avons également le théorème suivant : Soit c un élément de E2n écrit sous la forme c=2kc' , c' impair. Pour qu'il existe une antichaîne de E2n de cardinal n contenant c il faut et il suffit que 2n  < 3k + 1 c' .

Références

Ce document provient de « Anticha%C3%AEne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Antichaine de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Antichaîne — En mathématiques, plus précisément en théorie des ordres, une antichaîne d un ensemble E muni d une relation d ordre (notée ici ≤ ) est une partie A de E telle que Autrement dit, dans un ensemble ordonné, une antichaîne est une partie dont les… …   Wikipédia en Français

  • Forcing — En mathématiques, et plus précisément en logique mathématique, le forcing est une technique inventée par Paul Cohen pour prouver des résultats de cohérence et d indépendance en théorie des ensembles. Elle a été utilisée pour la première fois en… …   Wikipédia en Français

  • Famille De Sperner — En combinatoire, une famille de Sperner (ou système de Sperner), appelé en l honneur d Emanuel Sperner, est système d ensembles (F, E) dans lequel aucun élément ne contient un autre. Formellement, Si X, Y sont dans F et X ≠ Y, alors X n est pas… …   Wikipédia en Français

  • Famille de Sperner — En combinatoire, une famille de Sperner (ou système de Sperner), appelé en l honneur d Emanuel Sperner, est un hypergraphe (E, F) (c est à dire un ensemble E et un ensemble F de parties de E) dans lequel aucun élément de F ne contient un autre.… …   Wikipédia en Français

  • Famille de sperner — En combinatoire, une famille de Sperner (ou système de Sperner), appelé en l honneur d Emanuel Sperner, est système d ensembles (F, E) dans lequel aucun élément ne contient un autre. Formellement, Si X, Y sont dans F et X ≠ Y, alors X n est pas… …   Wikipédia en Français

  • Section commençante — Le treillis de l ensemble des parties de l ensemble {1,2,3,4}, la section finissante étant colorée en vert. En mathématiques, et plus précisément en théorie des ordres, une section commençante (parfois également appelée sous ensemble fermé… …   Wikipédia en Français

  • ENSEMBLES (THÉORIE DES) - Théorie axiomatique — La théorie des ensembles fut créée par Georg Cantor à la fin du XIXe siècle. Cependant, le caractère extrêmement général et abstrait de la notion d’ensemble permit de produire des paradoxes rendant la théorie contradictoire (cf. théorie… …   Encyclopédie Universelle

  • Relation d'ordre — Une relation d’ordre dans un ensemble est une relation binaire dans cet ensemble qui permet de comparer ses éléments entre eux de manière cohérente. Un ensemble muni d’une relation d’ordre est un ensemble ordonné ou tout simplement un ordre.… …   Wikipédia en Français

  • Bel ordre — En mathématiques, plus précisément en théorie des ordres, un bel ordre ≤ sur un ensemble X est un ordre partiel sur X tel que, pour toute suite d éléments de X, il existe i et j tels que i < j et xi ≤ xj. Autrement dit, c est un ordre partiel …   Wikipédia en Français

  • Théorème de Robertson-Seymour — En mathématiques, et plus précisément en théorie des graphes, le théorème de Robertson–Seymour (parfois également appelé le théorème des mineurs, et connu, avant qu il soit démontré, sous le nom de conjecture de Wagner), est un théorème démontré… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”