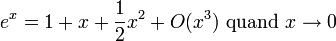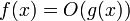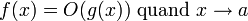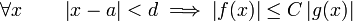Comparaison Asymptotique

Comparaison asymptotique

Pour les articles homonymes, voir Landau.

En mathématiques et en informatique, la comparaison asymptotique de deux fonctions (ou de deux suites, etc.) consiste à étudier (le plus souvent au voisinage de l'infini) la limite du quotient de ces deux fonctions : on dit par exemple que f est négligeable par rapport à g si la limite de f/g est nulle. Cet article décrit les différentes situations rencontrées, et les notations qui les désignent (il s'agit ici des notations de Landau ; les notations de Hardy sont décrites dans un autre article).

Sommaire

1 Notation grand O
2 Applications analytiques
3 Autres notations asymptotiques: O, o, Ω, ω, Θ, Õ
4 Fonction à plusieurs variables
5 Notations de Hardy
6 Voir aussi

Notation grand O

La notation grand O (avec la lettre majuscule O, et non pas zéro), aussi appelée symbole de Landau, est un symbole utilisé en mathématiques, notamment en théorie de la complexité pour décrire le comportement asymptotique des fonctions. Intuitivement, elle indique avec quelle rapidité une fonction « augmente » ou « diminue ».

Le symbole de Landau porte le nom du mathématicien allemand spécialisé en théorie des nombres Edmund Landau qui utilisa cette notation introduite primitivement par Bachmann. La lettre O est utilisée parce que la course de la « croissance » d'une fonction est aussi appelée l'ordre.

Par exemple, en analysant un algorithme, nous pourrions trouver que le temps (habituellement compté comme le nombre d'étapes) nécessaire afin de résoudre un problème de taille n est donné par T(n) = 4 n² - 2 n + 2. En ignorant les constantes (ce qui est fondé car elles dépendent du matériel particulier sur lequel le programme s'exécute) et les termes qui croissent le plus lentement, nous pourrions dire « T(n) croît comme n² » ou « T(n) est de l'ordre de n² » et nous écririons:T(n) = O(n²).

En mathématiques, il est souvent important de garder un œil sur le terme d'erreur d'une approximation. Cette notation est particulièrement utilisée dès que l'on a affaire à des développements limités et à des calculs d'équivalents. Par exemple, le développement de la fonction exponentielle à l'ordre 2 peut aussi s'écrire:

$e^x = 1+x+\frac{1}{2} x^2+O(x^3) \ {\rm quand}\ x \rightarrow 0$

pour exprimer le fait que l'erreur, la différence 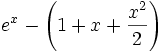$e^x - \left(1 + x +\frac{x^2}{2}\right)$ , est plus petite en valeur absolue qu'une constante fois 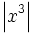$\left|x^3\right|$ quand $x$ tend vers 0.

Pour une définition rigoureuse, supposons que f et g soient deux fonctions définies sur une partie de l'ensemble des nombres réels. Nous écrivons :

$f(x) = O(g(x))\;$

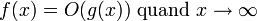(ou $f(x) = O(g(x)) \ {\rm quand}\ x\rightarrow\infty\;$ pour être plus précis) si et seulement s’il existe des constantes $N$ et $C$ telles que

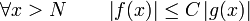$\forall x>N\qquad \left|f(x)\right| \le C \left|g(x)\right|$ .

Intuitivement, cela signifie que f ne croît pas plus vite que g.

De même, si $a$ est un nombre réel, nous écrivons

$f(x) = O(g(x)) \ {\rm quand}\ x \rightarrow a\;$

si et seulement s’il existe des constantes $d > 0$ et $C$ telles que

La première définition est la seule utilisée en informatique (où typiquement seules les fonctions positives à variable entière n sont considérées, les valeurs absolues pouvant être ignorées), tandis que les deux définitions sont utilisées en mathématiques.

Dans le même esprit de manipulation des ordres de grandeur, la notation $f (x) = o (g (x))$ (cette fois avec un petit o) signifie que la fonction f est négligeable devant la fonction g, quand x tend vers une valeur particulière.

Formellement, pour 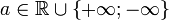$a \in \mathbb{R} \cup \left\{ +\infty ; -\infty \right\}$ ,et pour f et g deux fonctions de la variable réelle x, avec g qui ne s'annule pas sur un voisinage de a, on dit que

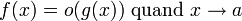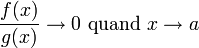$f(x) = o(g(x))\ {\rm quand}\ x \rightarrow a\;$ si et seulement si $\frac{f(x)}{g(x)} \rightarrow 0 \ {\rm quand}\ x \rightarrow a\;$ .

Applications analytiques

Voici une liste de catégories de fonctions qui sont couramment rencontrées dans les analyses d'algorithmes. Les fonctions sont classées par ordre de croissance de la plus lente à la plus rapide. c est une constante arbitraire.

notation		complexité
O(1)		constante
O(log(n))		logarithmique
O((log(n))^c)		polylogarithmique
O(n)		linéaire
O(n log(n))		parfois appelée « linéarithmique », ou « quasi-linéaire »
O(n²)		quadratique
O(n^c)		polynomiale, parfois « géométrique »
O(cⁿ)		exponentielle
O(n!)		factorielle

O(n^c) et O(cⁿ) sont très différents. Le dernier exprime une croissance bien plus rapide, et ce pour n'importe quelle constante c>1. Une fonction qui croît plus rapidement que n'importe quel polynôme est appelée super-polynomiale. Une fonction qui croît plus lentement que toute exponentielle est appelée sous-exponentielle. Il existe des fonctions à la fois super-polynômiales et sous-exponentielles comme par exemple la fonction n^log(n). Certains algorithmes ont un temps de calcul de ce type, comme celui de la factorisation d'un nombre entier.

Remarquons aussi, que O(log n) est exactement identique à O(log(n^c)). Les logarithmes diffèrent seulement d'un facteur constant, et que la notation grand O « ignore » les constantes. De manière analogue, les logarithmes dans des bases constantes différentes sont équivalents.

La liste précédente est utile à cause de la propriété suivante : si une fonction f est une somme de fonctions, et si une des fonctions de la somme grimpe plus vite que les autres, alors celle qui croît le plus vite détermine l'ordre de f(n).

ex.: si f(n) = 10 log(n) + 5 (log(n))³ + 7 n + 3 n² + 6 n³, alors f(n) = O(n³).

Autres notations asymptotiques: O, o, Ω, ω, Θ, Õ

Grand-O est la notation asymptotique la plus utilisée (souvent d'ailleurs pour signifier Θ (voir tableau plus bas)

Notation	Définition	Définition courte	Définition avec quantificateurs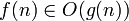
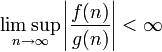
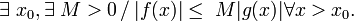
$f(n) \in O(g(n))$	dominée asymptotiquement	$\limsup_{n \to \infty} \left\|\frac{f(n)}{g(n)}\right\| < \infty$	$\exists \;x_0,\exists \;M>0 \, /\, \|f(x)\| \le \; M \|g(x)\|\forall x>x_0.$
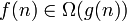
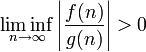
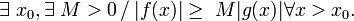
$f(n) \in \Omega(g(n))$	domine asymptotiquement	$\liminf_{n \to \infty} \left\|\frac{f(n)}{g(n)}\right\| > 0$	$\exists \;x_0,\exists \;M>0 \, / \, \|f(x)\| \ge \; M \|g(x)\|\forall x>x_0.$
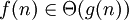
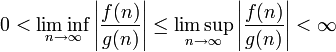
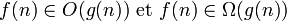
$f(n) \in \Theta(g(n))$	équivalence asymptotique	$0 < \liminf_{n \to \infty} \left\|\frac{f(n)}{g(n)}\right\| \leq \limsup_{n \to \infty} \left\|\frac{f(n)}{g(n)}\right\|< \infty$	$f(n) \in O(g(n)) \mbox{ et } f(n) \in \Omega(g(n))$
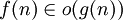
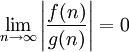
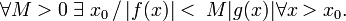
$f(n) \in o(g(n))$	asymptotiquement négligeable	$\lim_{n \to \infty} \left\|\frac{f(n)}{g(n)}\right\| = 0$	$\forall M>0 \; \exists \;x_0 \,/\, \|f(x)\| < \; M \|g(x)\| \forall x>x_0.$
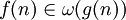
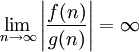
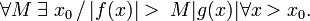
$f(n) \in \omega(g(n))$	asymptotiquement dominant	$\lim_{n \to \infty} \left\|\frac{f(n)}{g(n)}\right\| = \infty$	$\forall M \; \exists \;x_0 \,/\, \|f(x)\| > \; M \|g(x)\| \forall x>x_0.$

Après grand-O, les notations Θ et Ω sont les plus utilisées en informatique ; le petit-o est courant en mathématiques mais plus rare en informatique. Le ω est peu usité.

Une autre notation parfois utilisée en informatique est Õ (soft-O en anglais) qui signifie grand-o à un facteur logarithmique près.

Fonction à plusieurs variables

Nous pouvons signaler ici que le nombre d'opérandes dans la somme doit être constant et peut ne pas dépendre de n.

Cette notation peut aussi être utilisée avec des fonctions de plusieurs variables :

L'écriture:	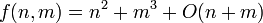$f(n,m) = n^2 + m^3 + O(n+m)\;$
correspond à la proposition:	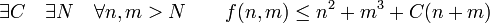$\exists C \quad \exists N \quad \forall n,m > N \qquad f(n,m) \le n^2 + m^3 + C(n+m)$

Évidemment, cette notation abuse du symbole d'égalité, puisque elle viole l'axiome d'égalité: « des choses égales à la même chose sont égales entre elles ». Pour être plus formellement correctes, certaines personnes préfèrent définir $O (g (x))$ comme un ensemble de fonctions, dont les éléments sont toutes les fonctions qui ne grandissent pas plus vite que g, et utilisent les notations ensemblistes pour indiquer si une fonction donnée est un élément de l'ensemble ainsi défini. Les deux conventions sont couramment utilisées mais la notation la moins soignée est jusqu'à présent la plus souvent rencontrée.

Un autre problème est que la variable par rapport à laquelle le comportement asymptotique est examiné n'est pas clairement indiquée. Une affirmation telle que 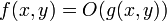$f(x,y) = O (g(x,y))\;$ exige quelques explications supplémentaires pour préciser ce que cela signifie. Cette difficulté se produit rarement dans la pratique.

Notations de Hardy

Article détaillé : notation de Hardy.

La question de la comparaison s'est d'abord posée en analyse, et d'un point de vue mathématique, on préfère généralement^{[réf. nécessaire]}la notation développée par Hardy, plus rigoureuse et évitant les ambiguités sur le signe d'égalité ou sur des calculs tels que o(x)+ o(x) = o(x). 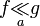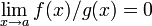Ainsi, ce que Landau note f=o(g) (l'endroit où la limite est calculée n'étant pas forcément indiqué, et dépendant du contexte) est défini par Hardy comme « f est négligeable par rapport à g en a », et noté $f \underset{a}\ll g$ (la signification restant la même, à savoir $\lim_{x\to a}f(x)/g(x)=0$ ).

Voir aussi

Notation de Hardy

Portail des mathématiques

Ce document provient de « Comparaison asymptotique ».

Catégories : Article en cours de recyclage | Analyse réelle | Vocabulaire des mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Comparaison Asymptotique de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Comparaison asymptotique — En mathématiques, plus précisément en analyse, la comparaison asymptotique est une méthode consistant à étudier le comportement d une fonction au voisinage d un point (ou en l infini), en regard du comportement d une autre fonction, souvent… … Wikipédia en Français
Comparaison Série-intégrale — Les séries sont un procédé de sommation de grandeurs discrètes, l intégrale de grandeurs continues. L analogie formelle entre les deux domaines permet de faire passer des idées intéressantes de l une à l autre. La comparaison explicite d une… … Wikipédia en Français
Comparaison serie-integrale — Comparaison série intégrale Les séries sont un procédé de sommation de grandeurs discrètes, l intégrale de grandeurs continues. L analogie formelle entre les deux domaines permet de faire passer des idées intéressantes de l une à l autre. La… … Wikipédia en Français
Comparaison série-intégrale — Les séries sont un procédé de sommation de grandeurs discrètes, l intégrale de grandeurs continues. L analogie formelle entre les deux domaines permet de faire passer des idées intéressantes de l une à l autre. La comparaison explicite d une… … Wikipédia en Français
Fonction asymptotique — En mathématiques, et plus précisément en analyse convexe, la fonction asymptotique (ou fonction de récession) est une fonction associée à une fonction convexe f et définie à partir d elle, qui a pour but de décrire son comportement à l infini. On … Wikipédia en Français
Développement asymptotique — En mathématiques, un développement asymptotique d une fonction f donnée dans un voisinage fixé est une somme finie de fonctions de références qui donne une bonne approximation du comportement de la fonction f dans le voisinage considéré. Le… … Wikipédia en Français
Developpement asymptotique — Développement asymptotique En mathématiques, un développement asymptotique d une fonction f donnée dans un voisinage fixé est une somme finie de fonctions de références qui donne une bonne approximation du comportement de la fonction f dans le… … Wikipédia en Français
Développement Asymptotique — En mathématiques, un développement asymptotique d une fonction f donnée dans un voisinage fixé est une somme finie de fonctions de références qui donne une bonne approximation du comportement de la fonction f dans le voisinage considéré. Le… … Wikipédia en Français
Grand O — Comparaison asymptotique Pour les articles homonymes, voir Landau. En mathématiques et en informatique, la comparaison asymptotique de deux fonctions (ou de deux suites, etc.) consiste à étudier (le plus souvent au voisinage de l infini) la… … Wikipédia en Français
Notation O — Comparaison asymptotique Pour les articles homonymes, voir Landau. En mathématiques et en informatique, la comparaison asymptotique de deux fonctions (ou de deux suites, etc.) consiste à étudier (le plus souvent au voisinage de l infini) la… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Comparaison Asymptotique