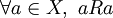Relation reflexive

Relation reflexive

Relation réflexive

En théorie des ensembles, une relation binaire peut avoir, entre autres deux propriétés, la réflexivité et l'irréflexivité.

  • Une relation réflexive R de l'ensemble X est une relation pour laquelle pour tout a de X, a est R-relié à lui-même. En notation mathématique, cela s'écrit :
\forall a \in X,\ a R a
  • Une relation irréflexive est une relation pour laquelle pour tout a de X, a n'est jamais R-relié à lui-même.

En notation mathématique, cela s'écrit :

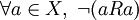\forall a \in X,\ \lnot (a R a).

Note: Irréflexivité est une condition plus forte que l'absence de réflexivité. Donc une relation peut être réflexive, irréflexive ou ni l'une ni l'autre. Les inégalités "strictement inférieur à" ou "strictement supérieur à" sont des relations irréflexives. Mais, si nous définissons une relation R sur les entiers telle que a R b si et seulement si a = -b, alors elle n'est ni réflexive, ni irréflexive, car 0 est le seul élément relié à lui-même.

Propriétés contenant la propriété réflexive

Préordre - Une relation réflexive qui est aussi transitive. Les différents types de préordres et de relations d'équivalence sont donc aussi réflexifs.

Exemples

Quelques exemples de relations réflexives:

  • "est égal à " (égalité)
  • "est un sous-ensemble de" (inclusion d'ensembles)
  • "est plus grand que ou égal à":
  • "est plus petit que ou égal à":
Fichier:GreaterThanOrEqualTo.png

Quelques exemples de relations irréflexives:

  • "n'est pas égal à"
  • "est copremier à"
  • "est strictement plus grand que":
Fichier:GreaterThan.png
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Relation r%C3%A9flexive ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Relation reflexive de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Relation réflexive — ● Relation réflexive relation binaire sur un ensemble telle que tout élément de cet ensemble soit en relation avec lui même …   Encyclopédie Universelle

  • Relation réflexive — Pour les articles homonymes, voir Réflexivité. En théorie des ensembles, une relation binaire peut avoir, entre autres deux propriétés, la réflexivité et l irréflexivité. Une relation réflexive R de l ensemble X est une relation pour laquelle… …   Wikipédia en Français

  • Relation antisymétrique — Relation binaire Une relation binaire est un concept mathématique qui systématise des notions comme « ... est supérieur ou égal à ... » en arithmétique, ou « ... est élément de l’ensemble ... » en théorie des ensembles. C’est… …   Wikipédia en Français

  • RELATION — Le concept de relation apparaît comme l’un des concepts fondamentaux du discours rationnel. Il semble lié à la pratique de l’analyse, qui constitue elle même l’un des aspects essentiels de la démarche discursive. L’analyse décompose les unités… …   Encyclopédie Universelle

  • Relation binaire — En mathématiques, une relation binaire entre deux ensembles E et F (ou simplement relation entre E et F) est caractérisée par un sous ensemble du produit cartésien E × F, soit une collection de couples dont la première composante est dans E et la …   Wikipédia en Français

  • réflexive — ● réflexif, réflexive adjectif (de réflexion) Se dit, en philosophie, de la conscience qui se prend elle même pour objet. ● réflexif, réflexive (expressions) adjectif (de réflexion) Relation réflexive, relation binaire sur un ensemble telle que… …   Encyclopédie Universelle

  • relation — Philosophically relations are interesting because of the historic prejudice, given its most forceful expression by Leibniz, that they are somehow ‘unreal’ compared to the intrinsic, monadic properties of things. A way of putting the idea is that… …   Philosophy dictionary

  • Relation d'equivalence — Relation d équivalence La notion de relation d équivalence sur un ensemble permet de mettre en relation des éléments qui sont similaires par une certaine propriété. On pourra ainsi regrouper ces éléments par « paquets » d éléments qui… …   Wikipédia en Français

  • Reflexive — may refer to:In fiction: MetafictionIn grammar: *Reflexive pronoun, a pronoun with a reflexive relationship with its self identical antecedent *Reflexive verb, where a semantic agent and patient are the sameIn mathematics and computer science:… …   Wikipedia

  • Relation algebra — is different from relational algebra, a framework developed by Edgar Codd in 1970 for relational databases. In mathematics, a relation algebra is a residuated Boolean algebra supporting an involutary unary operation called converse. The… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”