- Arbre (théorie des graphes)
-
Arbre (informatique)
 Pour les articles homonymes, voir Arbre (homonymie) .
Pour les articles homonymes, voir Arbre (homonymie) .En informatique, un arbre est une structure de données récursive générale, représentant un arbre au sens mathématique. C'est un cas particulier de graphe qui n'a qu'une seule source et aucun cycle.
Sommaire
vocabulaire
Dans un arbre, on distingue deux catégories d'éléments :
- les feuilles (ou nœuds externes), éléments ne possédant pas de fils dans l'arbre ;
- les nœuds internes, éléments possédant des fils (sous-branches).
La racine de l'arbre est l'unique nœud ne possédant pas de parent. Les nœuds (les pères avec leurs fils) sont reliés entre eux par une arête. Selon le contexte, un nœud peut désigner soit un nœud interne, soit un nœud interne ou externe (feuille) de l'arbre.
La profondeur d'un nœud est la distance, i.e. le nombre d'arêtes, de la racine au nœud[1]. La hauteur d'un arbre est la plus grande profondeur d'une feuille de l'arbre. La taille d'un arbre est son nombre de nœuds (en comptant les feuilles ou non), la longueur de cheminement est la somme des profondeurs de chacune des feuilles.
Les arbres peuvent être étiquetés. Dans ce cas, chaque nœud possède une étiquette, qui est en quelque sorte le « contenu » du nœud. L'étiquette peut être très simple : un nombre entier, par exemple. Elle peut également être aussi complexe que l'on veut : un objet, une instance d'une structure de données, un pointeur, etc. Il est presque toujours obligatoire de pouvoir comparer les étiquettes selon une relation d'ordre total, afin d'implanter les algorithmes sur les arbres.
Les fichiers et dossiers dans un système de fichiers sont généralement organisés sous forme arborescente. Voir par exemple la FHS.
Les arbres sont en fait rarement utilisés en tant que tels, mais de nombreux types d'arbres avec une structure plus restrictive existent et sont couramment utilisés en algorithmique, notamment pour gérer des bases de données, ou pour l'indexation de fichiers. Ils permettent alors des recherches rapides et efficaces. Nous vous en donnons ici les principaux exemples :
- Les arbres binaires dont chaque nœud a au plus deux fils : ils sont en fait utilisés sous forme d'arbres binaires de recherche, de tas, d'AVL, ou encore d'arbres rouge-noir. Les deux derniers exemples sont des cas particuliers d'arbres équilibrés, c'est-à-dire d'arbres dont les sous-branches ont presque la même hauteur.
- Les arbres n-aires qui sont une généralisation des arbres binaires : chaque nœud a au plus n fils. Les arbres 2-3-4 et les arbres B en sont des exemples d'utilisation et sont eux aussi des arbres balancés.
Construction
Pour construire un arbre à partir de cases ne contenant que des informations, on peut procéder de l'une des trois façons suivantes :
- Créer une structure de données composée de :
- l'étiquette (la valeur contenue dans le nœud),
- un lien vers chaque nœud fils,
- un arbre particulier, l'arbre vide, qui permet de caractériser les feuilles. Une feuille a pour fils des arbres vides uniquement.
- Créer une structure de données composée de :
- l'étiquette (la valeur contenue dans le nœud),
- un lien vers le « premier » nœud fils (nœud fils gauche le cas échéant),
- un autre lien vers le nœud frère (le « premier » nœud frère sur la droite le cas échéant).
- Créer une structure de données composée de :
- l'étiquette (la valeur contenue dans le nœud),
- un lien vers le nœud père.
On note qu'il existe d'autres types de représentation propres à des cas particuliers d'arbres. Par exemple, le tas est représenté par un tableau d'étiquettes.
Parcours
Parcours en largeur
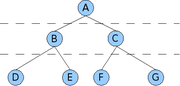
Le parcours en largeur correspond à un parcours par niveau de nœuds de l'arbre. Un niveau est un ensemble de nœuds internes ou[2] de feuilles situés à la même profondeur — on parle aussi de nœud ou de feuille de même hauteur dans l'arbre considéré. L'ordre de parcours d'un niveau donné est habituellement conféré, de manière récursive, par l'ordre de parcours des nœuds parents — nœuds du niveau immédiatement supérieur.
Ainsi, si l'arbre précédent est utilisé, le parcours sera A, B, C, D, E, F puis G.
Parcours en profondeur
Le parcours en profondeur est un parcours récursif sur un arbre. Il existe trois ordres pour cette méthode de parcours.
Parcours en profondeur préfixé
Dans ce mode de parcours, le nœud courant est traité avant le traitement des nœuds gauche et droit. Ainsi, si l'arbre précédent est utilisé, le parcours sera A, B, D, E, C, F puis G.
Parcours en profondeur infixé
Dans ce mode de parcours, le nœud courant est traité entre le traitement des nœuds gauche et droit. Ainsi, si l'arbre précédent est utilisé, le parcours sera D, B, E, A, F, C puis G.
Parcours en profondeur suffixé
Dans ce mode de parcours, le nœud courant est traité après le traitement des nœuds gauche et droit. Ainsi, si l'arbre précédent est utilisé, le parcours sera D, E, B, F, G, C puis A. Ce mode de parcours correspond à une notation polonaise inversée.
Exemples d'arbres
- Les arbres binaires;
- Les arbres B (B-Tree);
- Les arbres équilibrés;
- Les arbres syntaxiques;
- Les tas;
- Les arbres couvrants;
- Les octrees;
- Les Arbres AVL;
- Les Arbres bicolore.
Références
- ↑ Les arêtes d'un arbre peuvent être pondérés. Cette pondération peut servir à l'évaluation d'une mesure entre deux nœuds quelconques de l'arbre. On parle de longueur du (plus court) chemin entre deux nœuds d'un arbre, la longueur étant distincte de la différence des hauteurs respectives.
- ↑ Le « ou » est large : un niveau peut recouvrir à la fois des nœuds et des feuilles ; en effet, toutes les feuilles d'un arbre ne sont pas nécessairement situées à la même « distance » du nœud racine.
- Portail de la programmation informatique
Catégorie : Arbre (structure de données)
Wikimedia Foundation. 2010.