- Entrelacs et graphes
-
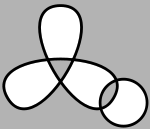
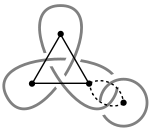
 Le triangle est associé avec le nœud de trèfle.
Le triangle est associé avec le nœud de trèfle.
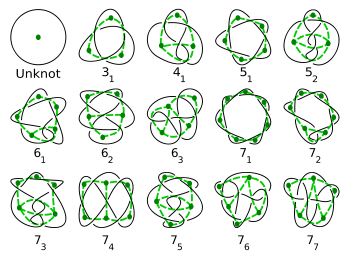
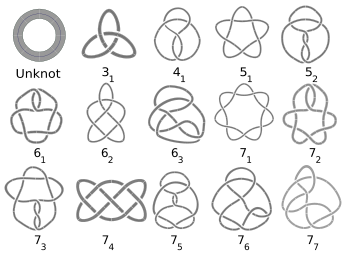
La théorie des nœuds et la théorie des graphes ont des rapports entre elles. Un entrelacs a l'air très compliqué mais est en fait codé par la structure simple de graphe planaire : des points (nommés sommets) reliés par des traits (nommés arêtes).
Sommaire
Diagramme de nœud
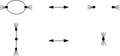
Un nœud ou entrelacs dans l'espace R3 peut être projeté sur le plan euclidien R2.
Cette projection est génériquement régulière, c'est-à-dire injective presque partout, à l'exception d'un nombre fini de points de croisements simples, où la projection envoie seulement 2 points de l'entrelacs au même endroit. De plus, les directions à ces deux points ne sont pas colinéaires si bien que les brins projetés pointent dans deux directions différentes du plan. Dans ces conditions, on indique quel brin est dessus et quel brin est dessous en interrompant le dessin. Un tel diagramme caractérise la classe d'isotopie de l'entrelacs.
En termes de théorie des graphes, un diagramme est simplement un graphe planaire de degré 4 (les sommets sont les croisements à quatre voisins) dont les sommets sont décorés par l'information des dessus-dessous.
Les mouvements de Reidemeister sont des modifications locales de ce graphe planaire décoré qui préservent la classe d'isotopie et permettent de passer de n'importe quelle projection à n'importe quelle autre.
Graphe médial
Une autre interprétation des diagrammes d'entrelacs facilite la manipulation d'un entrelacs : La projection décompose le plan en composantes connexes, le graphe lui-même, de dimension 1, et une zone infinie et des composantes homéomorphes à un disque, de dimension 2.
On peut attacher une couleur, noire ou blanche à chacune de ces zones de dimension 2 de la manière suivante : peignez en noire la zone infinie et, à chaque croisement, peignez en noire la zone opposée au croisement. Le théorème de Jordan implique que ce processus est bien défini.
 Guide +
Guide +
 Guide -
Guide -
Vous définissez ensuite un graphe planaire dont les sommets sont au "centre" de chaque zone blanche, et dont les arêtes "passent au-dessus" de chaque croisement. L'information du dessus-dessous est codé par un signe +/- décorant chaque arête. On peut représenter ce signe par la convention d'un trait plein pour un signe + et d'un trait en pointillé pour le signe -. Il y a un choix global de signe, un changement de ce choix correspond à la réflexion dans un miroir.
Mouvements de Reidemeister
Les mouvements de Reidemeister peuvent être traduits en ces termes : deux graphes planaires à arêtes signées sont associés au même entrelacs si on peut passer de l'un à l'autre par une série de mouvements de Reidemeister.
Dessiner de beaux entrelacs
Vous pouvez utiliser cette correspondance entre diagrammes d'entrelacs et graphes planaires pour dessiner de beaux entrelacs, pour les coder d'une manière plus aisée à manipuler, ou pour les déformer, les comparer ou les mémoriser.
Nous allons maintenant expliquer comment passer de la donnée du graphe planaire à celle du diagramme.
Par exemple l'art celte utilise souvent des entrelacs alternés, codés par des graphes planaires n'utilisant qu'un seul signe, dont les brins passent donc alternativement dessus-dessous. La méthode pour dessiner un entrelacs du type celte est la suivante :
- Dessinez un graphe planaire dont les arêtes sont approximativement de la même taille et d'angles ni trop obtus ni trop aigus.
- Placez un croisement au milieu de chaque arête.
- Connectez les brins entre eux en suivant une méthode tirée des labyrinthes (et que nous détaillons plus loin).
- Faites ressortir les dessus-dessous.
Passons au détail de chaque étape :
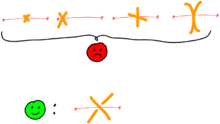
Placez un croisement au milieu de chaque arête
Cela peut sembler facile, mais il y a plusieurs façons de mal faire et une seule de bien faire : placez une croix de taille respectable, bien orientée, bien au milieu de chaque arête; pas d'un côté mais au milieu, pas à 90° mais à peu près 45°, les deux brins transverses entre eux et à l'arête et non pas tangents.
De cette manière, chaque brin pointe dans une direction bien définie.
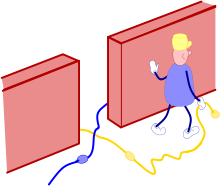
Reliez les brins
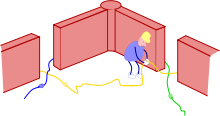
Pour savoir où relier un brin, imaginez votre graphe comme un labyrinthe où les arêtes sont des murs, fermés exceptés au milieu, où le croisement a lieu. Prenez un brin; si vous l'avez bien dessiné, il pointe dans une direction; suivez le mur dans cette direction, tournez au coin, suivez le mur de l'arête suivante, jusqu'à arriver au croisement; là, un brin pointe dans votre direction, c'est là qu'il faut s'arrimer.
Une fois que vous avez compris le trajet d'un brin, vous pouvez reprendre sa trajectoire; mais méfiez vous, n'introduisez pas ne nouveaux croisements : Chaque croisement au milieu de son arête et à chaque milieu d'arête son croisement! Ne passez pas non plus au travers des murs : les brins ne traversent les arêtes qu'en leur milieu, quand ils se croisent!
Décodez les dessus-dessous
Maintenant, recopiez le guide + ci-dessus sur un papier volant, de la taille de vos arêtes. Alignez l'arête du guide avec l'arête de votre graphe, par exemple en le posant par dessus. Il vous indiquera, entre les deux brins, lequel passe dessus, lequel passe dessous. Traitez chaque croisement, dans l'ordre que vous voulez, jusqu'à ce que tous soient déterminés.
En dernier lieu, gonflez chaque brin. Petit conseil : les scribes irlandais coloriaient non pas l'entrelacs lui-même mais le fond seulement.

Liens externes
(fr)/(en)/(de) Tutoriel sur les entrelacs
Wikimedia Foundation. 2010.