- Graphe Planaire
-
Graphe planaire
Dans la théorie des graphes, un graphe planaire est un graphe qui a la particularité de pouvoir se représenter sur un plan sans qu'aucune arête (ou arc pour un graphe orienté) n'en croise une autre. Autrement dit, ces graphes sont précisément ceux que l'on peut plonger dans le plan.
Les méthodes associées à ces graphes permettent de résoudre des problèmes comme l'énigme des trois maisons et d'autres plus difficiles comme le théorème des quatre couleurs.
Sommaire
Exemples et contre-exemples
1)
 2)
2) 3)
3) 4)
4)
- Ce graphe est clairement planaire, car il n'existe pas d'intersection entre deux arêtes.
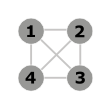
- C'est un graphe complet à quatre sommets (K4). Il est planaire : si on déplace le sommet 4 dans le triangle 1 2 3, on constate qu'il n'y a plus d'intersection d'arêtes.
- C'est un graphe complet à 5 sommets (K5). Il n'est pas planaire.
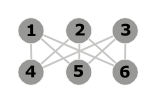
- C'est un graphe biparti complet à 6 sommets, 3 d'entre eux se connectant aux trois autres (K3,3). Il n'est pas planaire.
En fait, K5 et K3,3 sont les plus petits graphes non planaires, ce qui découle de la caractérisation ci-dessous.
Caractérisation de Kuratowski et de Wagner
Le mathématicien polonais Kazimierz Kuratowski a établi la caractérisation suivante des graphes planaires :
- Un graphe fini est planaire si et seulement s'il ne contient pas de sous-graphe qui est une expansion de K5 (la clique à 5 sommets) ou K3,3 (le graphe complet biparti à 3+3 sommets).
L'expansion d'un graphe est le résultat de l'ajout d'un ou plusieurs sommets sur une ou plusieurs arêtes (par exemple, transformation de l'arête •——• en •—•—•).
Quelques années plus tard le mathématicien allemand Klaus Wagner en donna une caractérisation semblable :
- Un graphe fini est planaire si et seulement s'il ne compte pas K5 ou K3,3 parmi ses mineurs.
Un mineur d'un graphe est le résultat de la contraction d'arêtes (fusionnant les extrémités), la suppression d'arêtes (sans fusionner les extrémités), et la suppression de sommets (et des arêtes adjacentes).
La différence entre ces deux caractérisations est minuscule, mais Wagner fit la conjecture que ce dernier admettrait une généralisation que celle de Kuratowski n'admettait pas. Il supposait qu'il y aurait, pour chaque classe de graphe fini close par mineur, un ensemble fini de mineurs interdits qui la caractériserait. Une classe est dite close par mineur si elle comprend tous les mineurs de chaque graphe qu'elle comprend ; un graphe planaire, par exemple, est toujours planaire après la contraction ou suppression d'arêtes et de sommets, et pour cette classe les deux seuls mineurs interdits sont K5 et K3,3. Mais aussi notamment il existerait un nombre fini de mineurs interdits pour la classe des graphes qui peuvent se plonger sur un tore, ou sur une surface quelconque, et pour la classe de graphes qui peuvent se plonger dans l'espace à trois dimensions sans noeud, entre autres. Cette conjecture fut enfin prouvée en 2004 par Robertson et Seymour, mais de façon non-constructive : par exemple, on ne connaît toujours pas tous les mineurs interdits pour le plongement de graphe sur un tore.
Propriétés
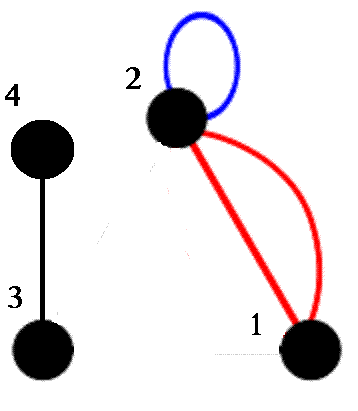
L'arête bleue est une boucle, les arêtes rouges sont multiples.
Dans toute la suite du paragraphe, G désigne un graphe planaire, n son nombre nœuds, a son nombre d'arêtes (ou de liens) et f son nombre de face. Une face est une composante connexe du complémentaire du graphe dans le plan. Le degré d'une face F est la longueur de son cycle frontière, on considère un chemin le plus court possible d'origine confondue avec son extrémité, le nombre d'arêtes (avec leur multiplicité) est le degré de la face F. Il est noté deg (F). On obtient une première formule presque évidente[1] :
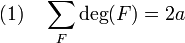
En effet, chaque arête élément d'un cycle borde deux faces, une arête partagée par aucun cycle est parcourue deux fois par le chemin frontière de la composante non bornée du complémentaire du graphe.
La formule d'Euler, pour un graphe planaire connexe est la suivante[2] :

Une méthode simple pour la démontrer est de l'établir pour un graphe sans cycle (à une face), puis par récurrence d'ajouter les arêtes qui engendrent des cycles. Cette formule permet de démontrer que tout graphe simple planaire connexe, ayant au moins trois sommets, vérifie la majoration suivante[3].
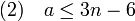
Un graphe simple est un graphe sans boucle (une boucle est une arête qui possède une origine et une extrémité confondues) et sans arête multiple (des arêtes multiples sont des arêtes ayant même origine et même extrémité). Cette formule se démontre simplement, toute face dispose d'un degré au moins égal à 3, car le graphe comporte au moins trois nœuds et est simple. On en déduit de la formule (1), que 3.f est inférieur ou égal à 2.a. La formule d'Euler permet de conclure.
Cette majoration est à l'origine d'une démonstration du fait que K5 n'est pas planaire. En effet, K5 dispose de 10 arêtes, et 5 nœuds, ce résultat est incompatible avec la majoration (2). Si, avec les hypothèses de la majoration (2), le graphe est sans triangle, on dispose alors de la majoration :
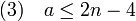
Le raisonnement est le même, mais cette fois-ci le degré d'une face est au moins égal à 4. On en déduit que K3,3 n'est pas planaire[3]. Les détails sont donnés dans l'article Énigme des trois maisons.
Démonstration de la formule d'EulerUn premier lemme est utile :
-
- Tout graphe planaire connexe peut s'obtenir en adjoignant des arêtes à un arbre connexe ayant les mêmes nœuds[4] :
Un arbre est un graphe ne contenant qu'une unique face. On procède par récurrence f le nombre de faces du graphe.
Supposons que le graphe ne possède qu'une unique face, le graphe est un arbre et la proposition est trivialement vérifiée. Supposons que la proposition vraie pour f et montrons là pour un graphe G à f + 1 faces. Le théorème de Jordan montre que s'il existe plusieurs faces, il existe une courbe de Jordan formée par des arêtes. Si l'on retranche une des arêtes A de la courbe au graphe G, les parties droite et gauche du complémentaire du graphe, qui formaient précédemment deux faces, n'en font plus qu'une et ce qui reste de la courbe de Jordan garantit que G est toujours connexe. Le graphe amputé de A vérifie les hypothèses de récurrence et s'obtient en adjoignant des arêtes à un arbre connexe. Ajouter la dernière arrête A fournit le graphe initial.
-
- Formule d'Euler[5] :
Démontrons la proposition tout d'abord pour un arbre, par récurrence sur n son nombre de nœuds. Si l'arbre ne contient qu'un unique nœud, il possède une face et aucune arête, la formule est vérifiée. On suppose que la formule est vraie pour n, montrons là pour un arbre G contenant n + 1 nœuds. Comme l'arbre ne contient qu'une unique face, il contient au moins un nœud N connecté à une unique arête (sinon le théorème de Jordan garantirait l'existence d'au moins deux faces.). L'arbre G ôté de ce nœud et de l'arête adjacente est un arbre connexe contenant n nœuds, il vérifie l'hypothèse de récurrence. Ajouter le nœud N et l'arête associé, correspond à ajouter un nœud et une arête, la formule d'Euler reste vraie pour G, ce qui termine cette première étape.
Démontrons maintenant la proposition pour un graphe connexe par récurrence sur f son nombre de faces. Si f est égal à 1, la formule est vérifiée d'après la récurrence précédente. Supposons la vraie pour tout arbre ayant f faces et montrons là pour un graphe G ayant f + 1 faces. La récurrence du lemme montre qu'il est possible de retrancher une arête à G de telle manière à ce que le nouveau graphe soit encore connexe et ait exactement f faces. La formule d'Euler est alors vérifiée par hypothèse de récurrence. Rajouter l'arête manquante ne modifie pas le nombre de nœuds, et incrémente de un le nombre d'arêtes et de faces. La formule d'Euler est encore vérifiée, ce qui termine la démonstration.
Intérêt
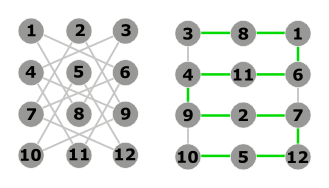 Un graphe de mouvement brut à gauche ; le même graphe réorganisé à droite
Un graphe de mouvement brut à gauche ; le même graphe réorganisé à droiteUn exemple simple pour illustrer l'intérêt des graphes planaires est une énigme, dite des trois maisons initialement posée sous forme mathématique par H. E. Dudeney en 1917[6]. Elle prend la forme suivante : Un lotissement de trois maisons doit être équipé d'eau de gaz et d'électricité. La règlementation interdit de croiser les canalisations pour des raisons de sécurité. Comment faut-il faire[7] ?
Cependant, l'intérêt pour les graphes planaires est plus ancien, il remonte au théorème des quatre couleurs. Depuis, de nombreux problèmes difficiles du point de vue algorithmique (NP-complet) se sont avérés faciles dans cette classe particulière ; toutefois pour la plupart de ces problèmes seule l'interdiction du mineur K5 est nécessaire.
La propriété de planarité est à l'origine des questions plus générales de plongement de graphe sur des surfaces (graph embedding) : peut-on plonger un graphe donné sur une surface donnée ?
La propriété de planarité d'un graphe le rend plus abordable au cerveau humain[réf. nécessaire] comme en témoigne l'exemple du problème du cavalier aux échecs ci-dessous :
- Sur un échiquier, on dispose un cavalier. Le but est de le faire passer par toutes les cases, une seule fois par case, en respectant le mouvement classique de la pièce aux échecs. Pour illustrer le problème, on utilise ici un plateau de quatre cases sur trois rangées. Le problème est représenté par un graphe de mouvement ; les sommets du graphe correspondent aux cases de l’échiquier ; les arcs figurent les mouvements possibles. Ainsi, à partir de la case 1, il est possible de se rendre à la case 8 ou à la case 6 car celles-ci sont liées à la première sur le graphe.
- Présenté de cette manière, le problème reste complexe. Toutefois, le graphe est planaire et on peut le représenter de façon plus intuitive. On peut facilement extraire de cette nouvelle représentation une solution (tracée en vert) partant de la case 3 et arrivant à la case 10.
De façon plus terre à terre, il était plus facile de concevoir les tout premiers circuits imprimés à transistors quand le graphe du circuit était planaire : on évitait alors de devoir recourir au procédé bicouche ou à des "straps" fragiles pour s'échapper du plan du circuit imprimé.
Références
- ↑ T. Chomettegraphe planaire p 1 Département de mathématiques appliquées École Normale Supérieure
- ↑ T. Chomettegraphe planaire p 4 Département de mathématiques appliquées École Normale Supérieure
- ↑ a et b (en) Wilfried Imrich et Sandi Klavzar - Product Graphs : Structure and recognition, Wiley-Interscience Series in Discrete Mathematics and Optimization, 2000.
- ↑ La proposition ainsi que la démonstration est disponible sur le site : T. Chomettegraphe planaire p 3 Département de mathématiques appliquées École Normale Supérieure
- ↑ Cette démonstration provient du site : T. Chomettegraphe planaire p 4 Département de mathématiques appliquées École Normale Supérieure
- ↑ M. Gardner The Sixth Book of Mathematical Games from Scientific American University of Chicago Press pp 92-94 (1984) (ISBN 0226282503)
- ↑ On la trouve sous le nom de problème des trois villas et des trois usines dans la référence : T. M. Dung Graphe planaire et problème de coloriage p. 10 Faculty of Information Technology Vietnam
Liens externes
- bibliothèque d'algorithmes et éditeur de graphes — bibliothèque d'algorithmes sur les graphes en GPL, parmi lesquels un test de planarité, une représentation planaire, une exhibition de sous-graphes de Kuratowski en temps linéaire.
- BGraphe — pour jouer avec les graphes planaires.
- Portail des mathématiques
Catégories : Concept en théorie des graphes | Famille de graphes
Wikimedia Foundation. 2010.