- Relation transitive
-
Transitivité (mathématiques)
En mathématiques, la transitivité est une propriété éventuelle d'une relation binaire. Une relation binaire
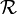 définie sur un ensemble E est transitive quand à chaque fois que l'on a trois éléments x, y et z de E tels que x et y sont en relation, ainsi que y et z, alors x et z sont en relation. Plus formellement :
définie sur un ensemble E est transitive quand à chaque fois que l'on a trois éléments x, y et z de E tels que x et y sont en relation, ainsi que y et z, alors x et z sont en relation. Plus formellement :![\forall x, y, z \in E\left[(x \mathcal{R} y \and y \mathcal{R} z) \implies x \mathcal{R} z\right]](/pictures/frwiki/56/86fbf7a325c8a1615bced0010ae3e7bd.png) .
.
Si l'amitié était transitive, on pourrait affirmer « Tous les amis de mes amis sont mes amis.»
On en déduit qu'une relation sur E n'est pas transitive si et seulement s'il existe un triplet d'éléments de E qui fournit un contre-exemple à la transitivité : x et y sont en relation, ainsi que y et z, mais pas x et z. Plus formellement :
![\exists x, y, z \in E\left[x \mathcal{R} y \and y \mathcal{R} z \and \lnot(x\mathcal{R}z)\right]](/pictures/frwiki/98/b567fdbd7832f7de8a211e41e22fd529.png) .
.
On dit alors que la relation binaire
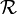 est non-transitive. Cette propriété, qui est la simple négation de la transitivité, ne doit pas être confondue avec la propriété suivante :
est non-transitive. Cette propriété, qui est la simple négation de la transitivité, ne doit pas être confondue avec la propriété suivante :![\forall x, y, z \in E \left[(x \mathcal{R} y \and y \mathcal{R} z) \implies\lnot(x \mathcal{R} z)\right]](/pictures/frwiki/54/6951c8ce600e4cd5383572cd8547a314.png) .
.
On dit parfois d'une telle relation qu'elle est anti-transitive (cette propriété est moins utile et moins courante que la transitivité, le vocabulaire n'est pas forcément bien établi). Remarquez que les propriétés de non-transitivité et d'anti-transitivité ne sont pas comparables (aucune des deux n'entraîne l'autre), et qu'une relation, même non vide, peut très bien être transitive et anti-transitive (il suffit qu'il n'y ait pas de triplet (x, y z) vérifiant x R y et y R z).
Sommaire
Exemples
- Les relations = ,
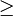 et
et 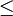 sont parmi quelques unes des relations transitives les plus couramment utilisées. Si a = b et si b = c alors automatiquement a = c.
sont parmi quelques unes des relations transitives les plus couramment utilisées. Si a = b et si b = c alors automatiquement a = c.
- La relation de parallélisme est transitive : si une droite D est parallèle à D', elle-même parallèle à D", alors D est parallèle à D". Il en est de même pour toute relation d'équivalence.
- De même, les relations d'ordre sont transitives. Par exemple,
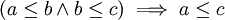 ou encore tout diviseur naturel d'un diviseur naturel de n divise n.
ou encore tout diviseur naturel d'un diviseur naturel de n divise n.
- Ainsi, on dit de la relation de congruence qu'elle est transitive dans
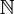 . Cela veut dire que si
. Cela veut dire que si ![a \equiv b [2]](/pictures/frwiki/51/3be102d93840d291624dba25c67a1eda.png) et si
et si ![b \equiv c [2]](/pictures/frwiki/55/7315e61145e9dc26a7a13fca056dfd6f.png) , alors
, alors ![a \equiv c [2]](/pictures/frwiki/56/8e8f712df2598a39ce661ccd850aac0f.png) .
.
Exemple de non-transitivité
- La relation
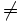 n'est pas transitive, c'est-à-dire
n'est pas transitive, c'est-à-dire 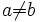 et
et 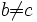 ne permet pas de dire que
ne permet pas de dire que 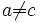 .
.
Exemple d'anti-transitivité
- La relation "est le père de" est anti-transitive : si (a est le père de b) et (b est le père de c), alors (a N'est PAS le père de c).
Voir aussi
- Portail de la logique
- Portail des mathématiques
Catégories : Théorie des ensembles | Logique mathématique
Wikimedia Foundation. 2010.
