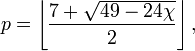Theoreme des quatre couleurs

Carte administrative de la Russie colorée avec quatre couleurs

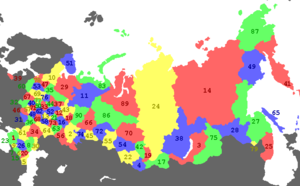
Le théorème des quatre couleurs affirme qu'il est possible, en n'utilisant que quatre couleurs différentes, de colorer^[1] n'importe quelle carte découpée en régions connexes, de sorte que deux régions adjacentes (ou limitrophes), c'est-à-dire ayant toute une frontière (et non simplement un point) en commun reçoivent toujours deux couleurs distinctes. L'énoncé peut varier et concerner, de manière tout à fait équivalente, la coloration des faces d'un polyèdre, ou des sommets d'un graphe planaire.

Trivialement, chacune des régions doit recevoir une couleur différente si les régions sont deux à deux adjacentes ; c'est le cas par exemple de la Belgique, du Luxembourg, de l'Allemagne et de la France dans une carte politique de l'Europe. D'où la nécessité des quatre couleurs dans le cas général. Par ailleurs, il ne peut exister cinq régions connexes deux à deux adjacentes (c'est la partie facile du théorème de Kuratowski).

Lorsqu'on généralise le problème à un graphe quelconque, il devient NP-complet de déterminer s'il est colorable avec seulement 4 couleurs (et même 3).

Histoire

Le résultat fut conjecturé en 1852 par Francis Guthrie, intéressé par la coloration de la carte des régions d'Angleterre. La première mention publiée date toutefois de 1879^[2]. Deux premières démonstrations furent publiées, respectivement par Alfred Kempe en 1879 et par Peter Guthrie Tait en 1880. Mais elles s'avèrent erronées ; les erreurs ont été relevées seulement en 1890 par Percy Heawood et en 1891 par Julius Petersen.

Ironiquement la fausse preuve de Kempe contient le schéma général de la vraie preuve. La fausse preuve fournit en fait une démonstration du résultat analogue mais avec cinq couleurs au lieu de quatre, aujourd'hui connu sous le nom du théorème des cinq couleurs (dont l'unique intérêt est d'admettre une courte preuve, donnée dans la référence), comme l'a remarqué Percy Heawood en 1890.

Dans les années 1960 et 1970, Heinrich Heesch s'intéresse à la possibilité de prouver informatiquement le théorème des quatre couleurs. Finalement, en 1976, deux Américains Kenneth Appel et Wolfgang Haken affirment avoir démontré le théorème des quatre couleurs. Leur démonstration partage la communauté scientifique : pour la première fois, en effet, la démonstration exige l'usage de l'ordinateur pour étudier les 1478 cas critiques (plus de 1200 heures de calcul). Le problème de la validation du théorème se trouve alors déplacé vers le problème de la validation :

• d'une part de l'algorithme d'exploration ;
• d'autre part de sa réalisation sous forme de programme.

Depuis 1976, l'algorithme d'Appel et Haken a été repris et simplifié par Robertson, Sanders, Seymour et Thomas^[3]. D'autres programmes informatiques, écrits de façon indépendante du premier, aboutissent au même résultat. Il existe ainsi une version entièrement formalisée, formulée avec Coq par Georges Gonthier et Benjamin Werner, qui permet à un ordinateur de complètement vérifier le théorème des quatre couleurs.

Paul Erdös pensait que le théorème des quatre couleurs était « un problème subtil et non pas un problème complexe ». D'après lui, une démonstration simple, et même très simple, devait exister. Mais pour cela, il aurait fallu peut-être « compliquer le problème », en le formulant pour un ensemble de points plus vaste qu'un graphe planaire, et incluant celui-ci. En tout cas, aucune preuve qui ne fasse pas appel à l'ordinateur n'a été découverte jusqu'ici ; cependant, de nombreux amateurs continuent à être convaincus de l'avoir démontré, et Underwood Dudley consacre un chapitre de Mathematical Cranks à ces tentatives, dont un exemple typique, et moins absurde que beaucoup d'autres, est celle de George Spencer-Brown, déposée en 1980^[4], mais qui n'a jamais été acceptée.

Généralisations du théorème des quatre couleurs

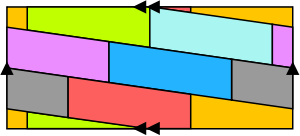En recollant les flêches simples et doubles ensemble (respectivement), on obtient un tore avec sept régions se touchant six à six ; ainsi, sept couleurs sont nécessaires

Cette image montre le résultat du collage précédent.

On peut aussi considérer le problème du coloriage de cartes tracées sur des surfaces autres que le plan. Sur la sphère, le problème est le même (pour le voir, il suffit de retirer un point de la sphère intérieur à l'une des régions, et d'effectuer une projection stéréographique). Pour des surfaces fermées de genre positif, le nombre maximum de couleurs nécessaires, p, dépend de la caractéristique d'Euler de la surface, χ, selon la formule

où les crochets extérieurs désignent la fonction partie entière.

Pour une surface orientable de genre g, cela revient à

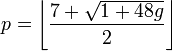(Eric Weisstein, Map coloring (en)).

Cette formule fut conjecturée par Heawood en 1890 et prouvée par Ringel et Youngs en 1968. On remarquera que pour g=0, elle redonne le théorème des quatre couleurs, mais bien sûr, les preuves précédentes ne s'appliquent qu'au cas où g>0.

Par exemple, le tore a une caractéristique d'Euler χ = 0 (et est de genre g = 1 : un tore n'a qu'un "trou") et donc p = 7 ; 7 couleurs suffisent donc pour colorer n'importe quelle carte sur le tore, et l'exemple de la figure montre que cela peut être nécessaire ; des exemples analogues permettent de montrer que la valeur de la conjecture de Heawood est la plus petite possible.

Il n'y a pas de généralisation évidente au même problème dans l'espace : en utilisant n tiges flexibles, il est possible de les arranger pour que chacune touche toutes les autres, et donc n peut être choisi aussi grand qu'on veut, sans qu'apparaisse un "théorème des n couleurs".

Passant à la théorie des graphes, on voit que l'énoncé classique du théorème des quatre couleurs n'est bien sûr pas une caractérisation des graphes dont le nombre chromatique est inférieur ou égale à 4 puisque le K_3,3 n'est pas planaire mais est biparti. D'autre part, pour des raisons de complexité algorithmique, il ne peut exister de caractérisation simple des graphes k-colorables pour k fixé supérieur à 3. Le théorème des quatre couleurs se généralise aux graphes sans mineur K₅, puisque le nombre chromatique de ces graphes vaut au plus 4 (et c'est une des motivations de la conjecture d'Hadwiger). Une généralisation plus forte encore a été donnée récemment par Guenin :

• les graphes sans mineur impair K₅ sont colorables avec seulement 4 couleurs.

(Un mineur est dit impair si les opérations de suppressions et de contractions des arêtes s'effectuent uniquement sur une coupe du graphe. Un graphe contient un mineur impair K₅ s'il contient un K₅ dont on a remplacé les dix arêtes par dix chemins de longueur impairs.)

Ces résultats plus forts sont basés sur des preuves utilisant le théorème des quatre couleurs lui-même, par conséquent ils n'en apportent pas de nouvelle démonstration.

Enfin (bien que le lien entre les deux questions soit peut-être faible), déterminer si un graphe (quelconque) peut être ou non coloré en 2 couleurs est très facile (techniquement, c'est un problème soluble en temps polynomial), mais en revanche, on sait que la 3-colorabilité d'un graphe quelconque (et donc bien sûr la k-colorabilité pour k>3) est un problème NP-complet. Toutefois, dans l'article mentionné en référence, Georges Gonthier fait remarquer que la preuve de Appel conduit à un calcul de coloration (avec quatre couleurs) d'un graphe planaire quelconque en temps non seulement polynomial, mais même quadratique.

Utilisation pratique

D’autres problèmes plus pratiques peuvent se réduire à la résolution de coloration de graphe, la solution peut alors être appliquée pour améliorer l'organisation de tâches.

• Affecter des fréquences différentes à des cellules voisines dans un réseau de téléphone mobile GSM.
• Organiser un examen suivant les matières que doit passer chaque étudiant. Comment mettre en parallèle plusieurs épreuves sans léser un candidat ?
• Optimiser l'utilisation des machines de travail. Comment mettre en parallèle des fabrications utilisant plusieurs machines ?
• Problème d'incompatibilité. Comment faire cohabiter des personnes ou animaux en tenant compte de leur incompatibilité ?

Notes et références

Liens externes

• Le théorème des quatre couleurs : un travail guidé (proposé par G. Gonthier, enseignant à Polytechnique), rappelant l'historique du théorème, et détaillant une amélioration de la méthode de Appel et Haken.

• Portail des mathématiques