Graphe biparti complet
- Graphe biparti complet
-
| Graphe biparti complet |
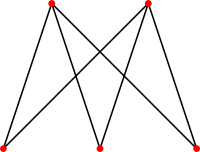
K3,2
|
| Notation |
Km,n |
| Nombre de sommets |
m + n |
| Nombre d'arêtes |
mn |
| Distribution des degrés |
m sommets de degré n
n sommet de degré m |
| Diamètre |
2 |
modifier  |
En théorie des graphes, un graphe est dit biparti complet (ou encore est appelé une biclique) s'il est biparti et contient le nombre maximal d'arêtes.
En d'autres termes, ils existe une partition de son ensemble de sommets en deux sous-ensembles U et V telle que chaque sommet de U est relié à chaque sommet de V.
Si U est de cardinal m et V est de cardinal n le graphe biparti complet est noté Km,n.
Propriétés
- Étant donné un graphe G, trouver le sous-graphe induit biparti complet Km,n de G avec le plus possible d'arêtes (donc avec mn maximal) est un problème NP-complet.
- Un graphe planaire ne peut pas contenir K3,3 comme mineur.
- Le graphe biparti complet Kn,n est un graphe de Moore et une (n,4)-cage.
- Les graphes bipartis complets Kn,n et Kn,n + 1 sont des graphes de Turán.
- Le graphe biparti complet Kn,n est un graphe symétrique : il est arête-transitif, sommet-transitif et arc-transitif.
Exemples
Si m=1 le graphe complet biparti Km,n est un arbre et est appelé une étoile. En tant qu'étoile, K1,n est notée Sn. Tous les graphes bipartis complets qui sont des arbres sont des étoiles.
Le graphe K3,3 est le plus petit graphe cubique non planaire. Il sert dans les caractérisation des graphes planaires de Kazimierz Kuratowski et de Klaus Wagner. C'est lui qui réside derrière l'énigme des trois maisons.
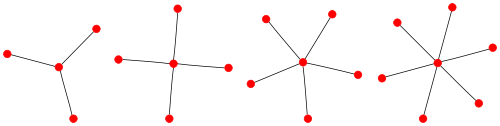
Les étoiles
S3,
S4,
S5 et
S6.
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Graphe biparti complet de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Graphe Biparti — Exemple de graphe biparti quelconque En théorie des graphes, un graphe est dit biparti s il existe une partition de son ensemble de sommets en deux sous ensembles U et V telle que chaque arête ait une extrémité dans U et l autre da … Wikipédia en Français
Graphe biparti — Exemple de graphe biparti quelconque En théorie des graphes, un graphe est dit biparti s il existe une partition de son ensemble de sommets en deux sous ensembles U et V telle que chaque arête ait une extrémité dans U et l autre dans … Wikipédia en Français
Biparti — Graphe biparti Exemple de graphe biparti quelconque En théorie des graphes, un graphe est dit biparti s il existe une partition de son ensemble de sommets en deux sous ensembles U et V telle que chaque arête ait une extrémité dans U et l autre da … Wikipédia en Français
Graphe bipartite — Graphe biparti Exemple de graphe biparti quelconque En théorie des graphes, un graphe est dit biparti s il existe une partition de son ensemble de sommets en deux sous ensembles U et V telle que chaque arête ait une extrémité dans U et l autre da … Wikipédia en Français
Graphe Complet — K5 Notation Kn Nombre de sommets n Nombre d arêtes n(n − 1) / 2 … Wikipédia en Français
Graphe Planaire — Dans la théorie des graphes, un graphe planaire est un graphe qui a la particularité de pouvoir se représenter sur un plan sans qu aucune arête (ou arc pour un graphe orienté) n en croise une autre. Autrement dit, ces graphes sont précisément… … Wikipédia en Français
Graphe complet — K5 Notation Kn Nombre de sommets n Nombre d arêtes … Wikipédia en Français
Graphe de Petersen — Schéma classique du graphe de Petersen, sous la forme d un pentagone et d un pentagramme concentriques, reliés par cinq rayons. Nombre de sommets 10 Nombre d arêtes 15 Distribution des degrés 3 régulier … Wikipédia en Français
Graphe partiel — Lexique de la théorie des graphes Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A … Wikipédia en Français
Graphe planaire — Dans la théorie des graphes, un graphe planaire est un graphe qui a la particularité de pouvoir se représenter sur un plan sans qu aucune arête (ou arc pour un graphe orienté) n en croise une autre. Autrement dit, ces graphes sont précisément… … Wikipédia en Français






