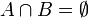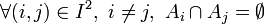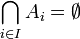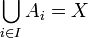Ensembles Disjoints

Ensembles disjoints

En mathématiques, deux ensembles sont dits disjoints s'ils n'ont pas d'éléments en commun. Par exemple, ${1,2,3}$ et ${4,5,6}$ sont deux ensembles disjoints.

Explication

De manière formelle, deux ensembles $A$ et $B$ sont disjoints si leur intersection est l'ensemble vide, c'est-à-dire si

$A\cap B = \emptyset$

Cette définition s'étends à une collection d'ensembles. Une collection d'ensembles disjoints deux à deux ou mutuellement disjoint si tout couple de 2 ensembles de cette collection sont disjoints.

Formellement, soit $I$ un ensemble indexé, et pour chaque 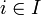$i \in I$ , on définit $A i$ comme un ensemble. Alors la famille d'ensembles 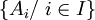$\{A_i/\ i\in I\}$ est mutuellement disjointe si

$\forall (i,j)\in I^2,\ i \neq j,\ A_i \cap A_j = \emptyset$

Par exemple, la famille de singletons ${{1},{2},{3}}$ est mutuellement disjointe.

Si ${A i}$ est une famille mutuellement dijointe, alors l'intersection de tous ses ensembles est vide:

$\bigcap_{i\in I} A_i = \emptyset$

Cependant, la réciproque est fausse: l'intersection de la famille ${{1,2},{2,3},{3,4}}$ est vide, mais cette famille n'est pas mutuellement disjointe.

Une partition $X$ est une famille de sous-ensembles non vides 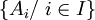$\{A_i/\ i\in I\}$ de $X$ telle que les $A i$ sont mutuellement disjoints et que :

$\bigcup_{i\in I} A_i = X$

Voir aussi

Ensembles presque disjoints
Connectivité
Union disjointe
Union-Find

Portail des mathématiques

Ce document provient de « Ensembles disjoints ».

Catégorie : Théorie des ensembles

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ensembles Disjoints de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Ensembles disjoints — En mathématiques, deux ensembles sont dits disjoints s ils n ont pas d éléments en commun. Par exemple, {1,2,3} et {4,5,6} sont deux ensembles disjoints. Explication De manière formelle, deux ensembles A et B sont disjoints si leur intersection… … Wikipédia en Français
ENSEMBLES (THÉORIE DES) - Théorie axiomatique — La théorie des ensembles fut créée par Georg Cantor à la fin du XIXe siècle. Cependant, le caractère extrêmement général et abstrait de la notion d’ensemble permit de produire des paradoxes rendant la théorie contradictoire (cf. théorie… … Encyclopédie Universelle
ENSEMBLES (THÉORIE DES) - Théorie élémentaire — L’algèbre des ensembles et l’étude abstraite des relations sont d’une importance croissante dans toutes les disciplines qui cherchent à s’exprimer dans un cadre rigoureux. En mathématiques, c’est l’interrogation sur les fondements de cette… … Encyclopédie Universelle
Operations sur les ensembles — Algèbre des parties d un ensemble Cet article est consacré à une première approche des opérations sur les ensembles et de leurs propriétés : réunion, intersection, différence, complémentation, différence symétrique... Sommaire 1 Réunion 1.1… … Wikipédia en Français
Theorie axiomatique des ensembles — Théorie des ensembles La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIXe siècle. La théorie des ensembles se donne comme primitives les notions d ensemble et d… … Wikipédia en Français
Theorie des ensembles — Théorie des ensembles La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIXe siècle. La théorie des ensembles se donne comme primitives les notions d ensemble et d… … Wikipédia en Français
Théorie axiomatique des ensembles — Théorie des ensembles La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIXe siècle. La théorie des ensembles se donne comme primitives les notions d ensemble et d… … Wikipédia en Français
Théorie des ensembles — La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIXe siècle. La théorie des ensembles se donne comme primitives les notions d ensemble et d appartenance, à partir… … Wikipédia en Français
Complementaire (theorie des ensembles) — Complémentaire (théorie des ensembles) Pour les articles homonymes, voir Complémentaire. Si le rectangle représente l ensemble E, la partie bleue est le complémentaire de la blanche … Wikipédia en Français
Complémentaire (Théorie Des Ensembles) — Pour les articles homonymes, voir Complémentaire. Si le rectangle représente l ensemble E, la partie bleue est le complémentaire de la blanche … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Ensembles Disjoints