- Plan projectif
-
La notion de plan projectif a deux sens distincts, qui se recoupent.
Sommaire
Géométrie algébrique
Un plan projectif en géométrie algébrique est une variété, aussi appelée espace projectif de dimension 2. On peut associer un plan projectif aux corps de nombres (nombres réels, nombres complexes, quaternions), à l'algèbre de division des octonions et plus généralement à tout corps
 (y compris les corps finis de type
(y compris les corps finis de type  ou
ou  ).
).Topologiquement, le plan projectif réel s'obtient par recollement des côtés opposés d'un carré, orientés en sens contraire. Il s'obtient également en recollant le bord d'un disque sur le bord d'un ruban de Möbius. Une représentation géométrique de cet espace est donnée par exemple par la surface de Boy.
Géométrie combinatoire
En géométrie combinatoire, un plan projectif d'ordre n est un ensemble de points et de droites (c'est-à-dire de groupements de points qu'on appellera droites) tels que :
- Il y a n2 + n + 1 points et autant de droites.
- Chaque droite possède n + 1 points et chaque point appartient à n + 1 droites exactement.
- Deux droites distinctes se rencontrent en un seul point.
- Deux points distincts se rencontrent en une seule droite.
On peut construire de tels objets en prenant les points du plan projectif sur un corps fini au sens de la géométrie algébrique. Le nombre n est alors une puissance d'un nombre premier.
Axiomes et plans projectifs
Une particularité de la dimension 2 est que le plan projectif peut ne pas satisfaire la propriété de Desargues. Un plan projectif arguésien (satisfaisant la propriété de Desargues) est un plan sur un corps quelconque. Un plan projectif de Pappus satisfait de plus la propriété de Pappus, c'est un olan projectif construit sur un corps commutatif.
Plan projectif réel
Girard Desargues est le créateur de la géométrie projective, étude de propriétés qui se conservent par projection centrale : alignement, point de concours et birapport.
Intuitivement la droite projective est une droite affine complétée par un point, appelé point à l'infini. Elle est en bijection avec R ∪ {∞} (à ne pas confondre avec R ∪ {-∞, +∞}).
Le plan projectif est un plan affine complété par la droite à l'infini (l'ensemble de ces points à l'infini), de façon à ce que deux droites distinctes aient un point commun.
Dans ce plan sont vérifiées les propriétés de Pappus et Desargues.
Liens
Wikimedia Foundation. 2010.


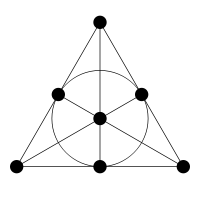
 . Il possède sept points et sept droites, dont une est représentée par un cercle.
. Il possède sept points et sept droites, dont une est représentée par un cercle.