- Tétraèdre
-
Tétraèdre 
Type Solide de Platon Type de faces 4×{3} Configuration de sommet 3.3.3 Faces 4 Arêtes 6 Sommets 4 Caractéristique 2 Symbole de Schläfli {3,3}
s{2,2}Symbole de Wythoff 3 | 2 3
| 2 2 2Diagramme de Coxeter-Dynkin 
Type de faces 4×{3} Références d'indexation U01, C15, W1 Dual Auto-dual Groupe de symétrie Uniforme, convexe, deltaèdre 
3.3.3
((Figure de sommet)
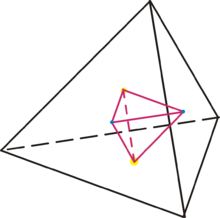
Auto-dual
(Dual)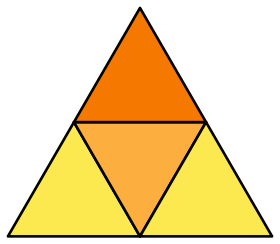
Patronmodifier 
Le tétraèdre (du grec tétra : quatre), est un polyèdre composé de quatre triangles, de la famille des pyramides, .
Le tétraèdre régulier, formé de quatre triangles équilatéraux, est l'un des cinq polyèdres réguliers, ou solides de Platon. C'est le seul d'entre eux à avoir quatre faces.
Le squelette du tétraèdre régulier, l'ensemble de ses sommets reliés par ses arêtes, forme un graphe appelé graphe tétraédrique.
Un tétraèdre est dit orthocentrique lorsque ses quatre hauteurs sont concourantes. Le point de concours est alors l'orthocentre du tétraèdre.
Le tétraèdre est un simplexe de degré 3.
Volume du tétraèdre
si B est la surface d'une base du tétraèdre et h la hauteur du tétraèdre s'appuyant sur cette base
pour le tétraèdre construit sur A, B, C et D.Tétraèdre régulier
Article détaillé : Tétraèdre régulier.Si a est la longueur d'une arête :
- La surface est égale à :
- La hauteur est égale à :
- Le centre du tétraèdre est situé, par rapport à la base, à :
- Le volume est égal :
- La valeur de l'angle central du tétraèdre régulier (c’est-à-dire celui que forment tous les segments qui partent du centre vers les quatre sommets) est de
(approx. 109.471°).
Dualité du tétraèdre régulier
Le tétraèdre est son propre dual, c'est-à-dire qu'en joignant les centres des faces d'un tétraèdre régulier, on obtient un nouveau tétraèdre régulier.
Le groupe des isométries laissant globalement invariant le tétraèdre régulier est isomorphe au groupe symétrique
. Le groupe des isométries positives ayant cette même propriété est quant à lui isomorphe au groupe alterné 
. Une démonstration est proposée dans l'article Groupe alterné. - La surface est égale à :
Wikimedia Foundation. 2010.
