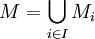- Théorème de hahn-banach
-
Théorème de Hahn-Banach
Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l'existence d'une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l'espace, mais limitées partout).
En permettant de prouver abstraitement l'existence de nombreuses fonctions continues, c'est un outil fondamental de l'analyse fonctionnelle.
Par son interprétation géométrique en termes d'hyperplans évitant un convexe fixé, il joue également un rôle primordial dans l'étude de la géométrie des convexes, et au-delà en analyse convexe.
Sommaire
Forme analytique et forme géométrique
Les énoncés dénommés « théorème de Hahn-Banach » dans la littérature scientifique sont nombreux, différant les uns des autres parfois par de simples détails et parfois de façon significative. Ils se divisent néanmoins nettement en deux classes : certains garantissent de pouvoir prolonger une forme linéaire, sous certaines exigences de majoration (les formes « analytiques » du théorème) ; d'autres assurent qu'on peut séparer deux ensembles convexes par un hyperplan affine (les formes « géométriques » du théorème).
Donnons pour commencer un exemple d'énoncé pour chacune de ces deux catégories[1].
Un énoncé de la forme analytique du théorème
Théorème — Soit V un espace vectoriel sur
 et p une fonction convexe définie sur V et qui ne prend que des valeurs finies.
et p une fonction convexe définie sur V et qui ne prend que des valeurs finies.Soit G un sous-espace vectoriel de V, et f une forme linéaire sur G qui y vérifie en tout point la condition de majoration :
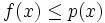 .
.Il existe alors un prolongement de f en une forme linéaire sur l'espace V tout entier, vérifiant encore la condition :
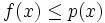 en tout point de V.
en tout point de V.Un énoncé de la forme géométrique du théorème
Théorème — Soit E un espace vectoriel topologique et C un convexe ouvert non vide de E.
Soit L un sous-espace affine de E qui vérifie la condition :
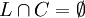 .
.Il existe alors un hyperplan affine H contenant L et qui vérifie lui aussi la condition :
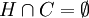 .
.De plus, H est un hyperplan fermé.
La forme analytique du théorème est due à Banach[2] (1932) généralisant un résultat de Hahn qui s'intéresse dès 1920 aux espaces vectoriels normés. Il existe une généralisation du théorème de Hahn-Banach aux espaces vectoriels sur le corps des complexes[3] due à Bohnenblust et Sobczyk (1938). Les difficultés de la généralisation du théorème de Hahn-Banach apparaissent même pour des espaces vectoriels de dimension finie.
Relations entre les deux énoncés et preuve de la forme « géométrique »
La forme géométrique du théorème —d'où on peut ensuite déduire une succession de variantes diverses relatives à la séparation des convexes— est la retranscription de la forme analytique pour le cas particulier où la fonction convexe qui y intervient est la jauge d'un ouvert convexe d'un espace normé. C'est d'ailleurs le cas dans les utilisations les plus simples et fondamentales du théorème en analyse fonctionnelle qu'on peut selon ses goûts lire depuis une version ou l'autre (on en verra un exemple plus bas).
Voyons de plus près comment la forme géométrique se déduit de la forme analytique :
Démonstration de la forme géométrique à partir de la forme analytiqueQuitte à faire préalablement une translation, on supposera que l'origine est dans C. Dès lors, puisque L ne rencontre pas C, c'est donc un sous-espace affine évitant l'origine.
Notons p la jauge du convexe C. Elle est sous-linéaire et donc convexe comme toute jauge ; par définition même d'une jauge il est évident que pour tout x dans C,
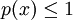 . Comme on a supposé C ouvert, on peut aller un peu plus loin : d'une part C est un voisinage de 0 et toute demi-droite ouverte issue de 0 contient donc des points de C, ce dont on déduit que p ne prend pas la valeur
. Comme on a supposé C ouvert, on peut aller un peu plus loin : d'une part C est un voisinage de 0 et toute demi-droite ouverte issue de 0 contient donc des points de C, ce dont on déduit que p ne prend pas la valeur  ; d'autre part on peut améliorer l'inégalité large
; d'autre part on peut améliorer l'inégalité large 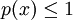 et préciser sans peine que les points de C sont caractérisés par l'inéquation stricte p(x) < 1. Voilà pour la fonction sous-linéaire.
et préciser sans peine que les points de C sont caractérisés par l'inéquation stricte p(x) < 1. Voilà pour la fonction sous-linéaire.Notons G le sous-espace vectoriel engendré par L. Puisque
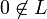 , la sous-variété affine L est de codimension 1 dans G et il existe une (et une seule) forme linéaire f sur G telle que L soit la partie de G d'équation f(x) = 1. Voilà pour la forme linéaire à prolonger.
, la sous-variété affine L est de codimension 1 dans G et il existe une (et une seule) forme linéaire f sur G telle que L soit la partie de G d'équation f(x) = 1. Voilà pour la forme linéaire à prolonger.Enfin, pour x dans L,
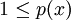 (puisque
(puisque 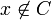 ) tandis que f(x) = 1. La condition
) tandis que f(x) = 1. La condition 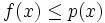 est donc vérifiée sur L. En jouant sur l'homogénéité positive de f et de p, on étend son domaine de validité à un demi-espace strict de G ; sur l'autre demi-espace f prend des valeurs négatives ou nulles tandis que, comme partout, p est à valeurs positives ou nulles. L'inégalité
est donc vérifiée sur L. En jouant sur l'homogénéité positive de f et de p, on étend son domaine de validité à un demi-espace strict de G ; sur l'autre demi-espace f prend des valeurs négatives ou nulles tandis que, comme partout, p est à valeurs positives ou nulles. L'inégalité 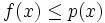 est donc vraie partout dans G.
est donc vraie partout dans G.Toutes les hypothèses de la version dite « analytique » du théorème sont en place. Appliquons la donc. Elle nous offre une nouvelle forme linéaire encore notée f, cette fois définie sur E tout entier. Notons H l'hyperplan affine d'équation f(x) = 1 : par construction, c'est bien un hyperplan contenant L.
Soit maintenant un point x de C : pour ce point,
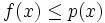 (puisque f a été produite par la forme analytique de Hahn-Banach) et p(x) < 1 (puisqu'on est dans l'ouvert convexe C). Donc
(puisque f a été produite par la forme analytique de Hahn-Banach) et p(x) < 1 (puisqu'on est dans l'ouvert convexe C). Donc 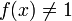 , et x n'est pas dans H. On a bien vérifié que C et H ne se rencontrent pas.
, et x n'est pas dans H. On a bien vérifié que C et H ne se rencontrent pas.Enfin les hyperplans d'un espace vectoriel topologique sont nécessairement fermés ou denses. Or H n'est pas dense puisqu'il ne rencontre pas le voisinage C de 0. C'est donc qu'il est fermé.
On peut s'étonner que la forme géométrique fasse intervenir une topologie tandis que la forme analytique concerne un espace vectoriel sans structure additionnelle. En fait, il est tout à fait possible d'énoncer une forme géométrique dans un espace vectoriel quelconque : il faudra alors supposer que tout translaté du convexe C contenant l'origine est absorbant, à défaut de pouvoir donner un sens à « ouvert » ; on n'a bien sûr plus le complément sur le caractère fermé de l'hyperplan obtenu tombe. La démonstration est la même.
La preuve de la forme « analytique »
Deux types d'idées bien distinctes sont à mettre bout à bout pour aboutir à une preuve dans le cadre de généralité où le théorème a été énoncé. Dans un premier temps, quelques calculs assez simples permettent de justifier l'extension de la forme linéaire f dans le cas particulier où G est de codimension 1 dans V. Une fois cette étape franchie, on a déjà le théorème en dimension finie (il suffit de faire grossir pas à pas le sous-espace où on a réussi à étendre f, d'une dimension à chaque pas, et jusqu'à atteindre la dimension de V). En revanche, pour les usages en dimension infinie, il faut adapter cette méthode fort simple d'avancée méthodique et appeler quelques techniques assez standardisées de théorie des ensembles : on exécute ainsi une récurrence transfinie, le plus souvent rédigée sous forme d'un appel au lemme de Zorn.
Détail de la démonstrationPremière partie : gagner une dimension
Dans un premier temps, on va prolonger la forme linéaire f à un espace plus grand que G en gagnant une dimension. Prenons un élément v0 de V en dehors de G (s'il n'y en a pas G = V et on a terminé avant même d'avoir commencé).
Le prolongement de f au sous-espace vectoriel
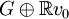 s'opère en la définissant par la formule :
s'opère en la définissant par la formule :dans laquelle α est un réel qu'il va falloir choisir judicieusement pour que la condition de majoration de f reste vérifiée dans
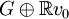 .
.Il est clair que cette méthode d'extension fournit une forme linéaire, quel que soit le choix de α.
La condition de majoration sera vérifiée si et seulement si, pour chaque x de G et chaque λ réel, l'inégalité suivante est vérifiée :
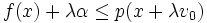 .
.
Après avoir noté que pour λ = 0 elle est justifiée par hypothèse, on peut ne s'intéresser qu'aux contraintes correspondant à
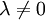 . Il est judicieux alors de séparer les conditions correspondant à λ > 0 et ceux où λ < 0 ; en notant μ = λ dans le premier cas, et μ = − λ dans le second, on a donc à vérifier deux familles d'inégalités :
. Il est judicieux alors de séparer les conditions correspondant à λ > 0 et ceux où λ < 0 ; en notant μ = λ dans le premier cas, et μ = − λ dans le second, on a donc à vérifier deux familles d'inégalités :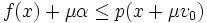 (où x parcourt G et μ parcourt
(où x parcourt G et μ parcourt 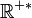 ).
).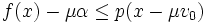 (où x parcourt G et μ parcourt
(où x parcourt G et μ parcourt 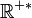 )
)
Des manipulations élémentaires permettent de les regrouper sous la forme :
Notons
![a_{x,\mu} = {1\over\mu}\left[f(x)-p(x-\mu v_0)\right]](/pictures/frwiki/55/7c6767a3fe78c1948e485069d1b4956e.png) et
et ![b_{x,\mu} ={1\over\mu}\left[p(x+\mu v_0)-f(x)\right]](/pictures/frwiki/48/009a6e5bd0aa2a4b5e8fd68ee319d1bd.png) les extrémités de l'inégalité précédente. La condition nécessaire et suffisante pour qu'on puisse définir un prolongement valable de f est ainsi que les intervalles [ax,μ;bx,μ] (où x parcourt G et μ parcourt
les extrémités de l'inégalité précédente. La condition nécessaire et suffisante pour qu'on puisse définir un prolongement valable de f est ainsi que les intervalles [ax,μ;bx,μ] (où x parcourt G et μ parcourt 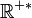 ) aient une intersection non vide. Or ceci est équivalent à :
) aient une intersection non vide. Or ceci est équivalent à :- pour tout
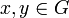 , et tous
, et tous 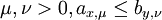 .
.
Mais cette condition est réalisée, par une vérification lourde mais facile qui exploite la convexité de p, la linéarité de f et la majoration supposée vraie sur G : en effet, pour x, y dans G et tous μ,ν > 0:
![b_{y,\nu} - a_{x,\mu} = {1\over\nu}\left[p(y+\nu v_0)-f(y)\right] - {1\over\mu}\left[f(x)-p(x-\mu v_0)\right]](/pictures/frwiki/50/2077d5bb4c374fd8e14ab94f1e3fafc7.png)
![={{\mu+\nu}\over{\mu\nu}}\left[{\nu\over{\mu+\nu}}p(x-\mu v_0)+{\mu\over{\mu+\nu}}p(y+\nu v_0)-{\nu\over{\mu+\nu}}f(x)-{\mu\over{\mu+\nu}}f(y)\right]](/pictures/frwiki/55/7088652ed1c5ea76fc1f1fd09d4adf5f.png)
![\geq{{\mu+\nu}\over{\mu\nu}}\left[p\left({\nu\over{\mu+\nu}}(x-\mu v_0)+{\mu\over{\mu+\nu}}(y+\nu v_0)\right)-f\left({{\nu x}\over{\mu+\nu}}+{{\mu y}\over{\mu+\nu}}\right)\right]](/pictures/frwiki/49/1f5c334341b6cf6bd19016bc1cf0a0f9.png)
![={{\mu+\nu}\over{\mu\nu}}\left[p\left({{\nu x+\mu y}\over{\mu +\nu}}\right)-f\left({{\nu x+\mu y}\over{\mu +\nu}}\right)\right]\geq 0](/pictures/frwiki/53/55e08b049880550c1abe845ea88923d8.png) .
.
Deuxième partie : exécution d'une récurrence transfinie
En raisonnant de proche en proche, on voit que l'on peut prolonger f à des espaces de plus en plus grands. Si G est de codimension finie dans V, alors le procédé ainsi défini s'arrête. Sinon, on utilise l'axiome du choix.
Pour cela, on considère l'ensemble des couples (M,g) dans lesquels M est un sous-espace vectoriel de V contenant G et g est une forme linéaire sur M prolongeant f (en respectant la contrainte de majoration par p), et on l'ordonne partiellement par :
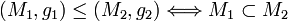 et
et 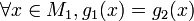 .
.
L'ensemble des couples est inductif. En effet si
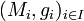 est une chaîne totalement ordonnée, alors on pose :
est une chaîne totalement ordonnée, alors on pose :M est un sous-espace vectoriel. (En général, une union d'espaces vectoriels n'est pas un espace vectoriel, en revanche, ici, c'est le cas car la famille des
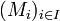 est totalement ordonnée).
est totalement ordonnée).On définit la forme linéaire g sur l'espace M par :
- g(x) = gi(x) si
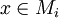 .
.
On vérifie aisément que cette définition de g est correcte. (M, g) est alors un majorant de la chaîne
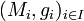 . Le lemme de Zorn s'applique, et on peut alors trouver un sous-espace N maximal sur lequel f se prolonge.
. Le lemme de Zorn s'applique, et on peut alors trouver un sous-espace N maximal sur lequel f se prolonge.Maintenant si N n'est pas égal à V, alors la première partie de la démonstration montre que l'on peut prolonger f (définie sur N) à un espace strictement plus grand que N, ce qui en contradiction avec la maximalité de N.
Un exemple d'application en analyse fonctionnelle
Le corollaire suivant illustre comment le théorème de Hahn-Banach peut produire très facilement des résultats essentiels d'analyse fonctionnelle[4].
Corollaire — Soit E un espace normé, G un sous-espace de E et f une forme linéaire continue sur G. On peut alors prolonger f en une application continue définie sur E, de même norme que f.
DémonstrationOn note
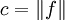 et on applique le théorème à la fonction convexe
et on applique le théorème à la fonction convexe 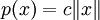 .
.Il est inutilement long mais instructif de résoudre la question en utilisant la forme géométrique du théorème de Hahn-Banach : au lieu de penser à la fonction convexe p, on peut aussi penser au convexe ouvert C dont elle est la jauge, à savoir la boule ouverte de centre 0 et de rayon 1 / c. Si on veut se lancer dans cette voie, il faut introduire alors le sous-espace affine L, ensemble des points de G où f(x) = 1. On l'étend en un hyperplan fermé en appliquant Hahn-Banach ; la forme linéaire continue g pour lequel cet hyperplan est l'ensemble d'équation g(x) = 1 répond alors au cahier des charges.
Quelques autres versions du théorème
On trouvera ci-dessous deux variantes de la « forme analytique » qui se déduisent facilement de celle mise en relief. La première fournit une variante du résultat pour les espaces vectoriels complexes ; la seconde précise que sous une bonne hypothèse de symétrie de p, notamment vérifiée quand p est une semi-norme, on peut obtenir une majoration de la valeur absolue (ou du module dans le cas complexe) de la forme linéaire prolongée[5].
Théorème — Soit V un espace vectoriel sur
 et p une fonction convexe définie sur V, qui ne prend pas la valeur
et p une fonction convexe définie sur V, qui ne prend pas la valeur  .
.Soit G un sous-espace vectoriel de V, et f une forme linéaire sur G qui y vérifie en tout point la condition de majoration :
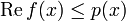 .
.Il existe alors un prolongement de f en une forme linéaire sur l'espace V tout entier, vérifiant encore la condition :
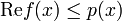 en tout point de V.
en tout point de V.Théorème — Soit V un espace vectoriel sur
 ou
ou  et p une fonction convexe définie sur V, qui ne prend pas la valeur
et p une fonction convexe définie sur V, qui ne prend pas la valeur  .
.On suppose en outre que p possède la propriété de symétrie suivante : pour tout scalaire θ avec | θ | = 1 et tout vecteur x de V, p(x) = p(θx).
Soit G un sous-espace vectoriel de V, et f une forme linéaire sur G qui y vérifie en tout point la condition de majoration :
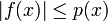 .
.Il existe alors un prolongement de f en une forme linéaire sur l'espace V tout entier, vérifiant encore la condition :
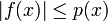 en tout point de V.
en tout point de V.On trouvera des variantes de la forme géométrique à l'article Séparation des convexes.
Le rôle de l'axiome du choix
Comme on l'a vu, le lemme de Zorn (équivalent à l'axiome du choix) entraîne le théorème de Hahn-Banach. En réalité, le lemme des ultrafiltres, qui est une proposition plus faible que l'axiome du choix, est suffisant pour démontrer le théorème de Hahn-Banach. Mais inversement, on sait depuis des travaux de D. Pinas de 1972 que le théorème de Hahn-Banach n'est pas suffisant pour démontrer le lemme des ultrafiltres. Ainsi, le théorème de Hahn-Banach n'est pas équivalent à l'axiome du choix dans le système d'axiomes de Zermelo-Fraenkel. On doit ajouter à cela que le seul système de Zermelo-Fraenkel n'est pas à lui seul suffisant pour démontrer Hahn-Banach, dont toute preuve doit donc reposer inévitablement sur une ou autre variante de l'axiome du choix.[6]
Références
Lorsqu'une note renvoie à un nom d'auteur sans plus de précisions, il s'agit d'un des ouvrages mentionnés ci-dessous en bibliographie.
- ↑ L'énoncé analytique est le théorème III-5 dans Reed-Simon, p. 75. La forme géométrique est le théorème 1, p. II-39 dans Espaces vectoriels topologiques de Nicolas Bourbaki, Masson, 1981, (ISBN 2225684103), où figure aussi la remarque qui suit l'énoncé.
- ↑ Théorie des opérations linéaires, Varsovie
- ↑ H.F. Bohnenblust, A. Sobczyk, Bull. Amer. Math. Soc[1]
- ↑ L'exemple donné ici est le corollaire 1-2 dans Brezis, p. 3.
- ↑ Ces deux versions sont issues d'un cours donné par Gabriel Nagy à l'Université du Kansas, dont les notes sont disponibles en ligne.
- ↑ Toutes ces informations sont disponibles dans Consequences of the Axiom of Choice, de Paul Howard et Jean E. Rubin, coll. « Mathematical surveys and monographs », vol. 59, American Mathematical Society, 1998 (ISBN 0821809776), qui renvoie notamment aux articles de D. Pinas, « Independence of the prime ideal theorem from the Hahn-Banach theorem », dans le Bulletin of the American Mathematical Society, 78 (1972) p. 203-248 et « The strength of the Hahn-Banach theorem », dans Proceedings of the Victoria Symposium on Nonstandard Analysis, coll. « Lecture notes in mathematics », vol. 369, Springer, Heidelberg, 1973. Pinas fournit deux modèles où Hahn-Banach est vrai alors que certaines formes de l'axiome du choix (lemme des ultrafiltres, axiome du choix dénombrable) ne le sont pas, l'un construit pour l'occasion, l'autre étant un modèle déjà connu construit par A. Levy en 1962 à d'autres fins dans lequel il prouve que Hahn-Banach est vérifié. Il prouve par ailleurs qu'il existe des contre-exemples à Hahn-Banach dans le fameux modèle de Solovay de Zermelo-Fraenkel (celui où tout ensemble de réels est Lebesgue-mesurable).
Bibliographie
- Hans Hahn : Über lineare Gleichungssysteme in linearen Räumen. In: Journal für die reine und angewandte Mathematik 157 (1927), p. 214-229.
- Stefan Banach : Sur les fonctionnelles linéaires. In: Studia Mathematica 1 (1929), p. 211-216.
- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
- Lawrence Narici et Edward Beckenstein, 'The Hahn–Banach Theorem: The Life and Times', Topology and its Applications, Volume 77, 2° édition (3 juin 1997) pp. 193-211. Un préprint est disponible en ligne.
- Michael Reed et Barry Simon, Functional Analysis, Section III.3. Academic Press, San Diego, 1980. (ISBN 0-12-585050-5).
- Walter Rudin, Analyse fonctionnelle [détail des éditions]
Théorèmes de l'analyse fonctionnelleThéorème d'Ascoli • Théorème de Baire • Théorème de Banach-Alaoglu • Théorème de Banach-Mazur • Théorème de Banach-Schauder • Théorème de Banach-Steinhaus • Théorème du graphe fermé • Théorème de Hahn-Banach • Théorème de Lax-Milgram
- Portail des mathématiques
Catégories : Espace vectoriel normé | Géométrie convexe | Analyse convexe | Théorème de mathématiques
Wikimedia Foundation. 2010.

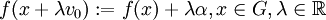
![{1\over\mu}\left[f(x)-p(x-\mu v_0)\right]\leq \alpha \leq {1\over\mu}\left[p(x+\mu v_0)-f(x)\right].](/pictures/frwiki/53/5f27220431653b286a094aba5db87128.png)